EXAMPLE 11 Randomized block design uncovers the significant differences among the learning methods
Note that the p-value for the blocking factor is approximately zero, which means that the blocking factor is significant. But in the randomized block design we are not interested in the significance of the blocking factor. If we are interested in a second factor, we use two-way ANOVA in Section 4.
Use technology and the randomized block design (RBD) to test for differences among the population mean test grades, at level of significance α=0.05.
Solution
We use the Step-by-Step Technology Guide at the end of this section to run this analysis in Minitab and SPSS. The hypotheses and the rejection rule are the same for RBD as they are for one-way ANOVA:
HO:μIn-class=μOnline=μHybrid versus Ha:not all the population means are equal
Reject H0 if the p-value≤0.05.
Figure 32 shows the Minitab output from the randomized block design, and Figure 33 shows the SPSS output. The factor of interest (that is, the treatment) is the learning method, whereas the blocking factor is the course. Note that there are two p-values, but we examine the p-value of the treatment only, not of the blocking factor.
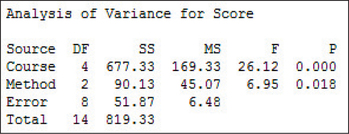
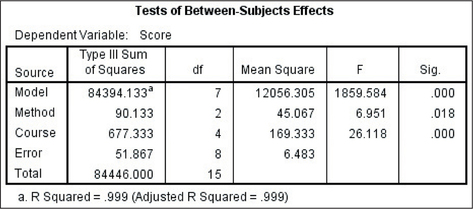
The p-value for the factor of interest from both Figure 32 and Figure 33 is 0.018, which is ≤0.05; therefore, we reject H0. There is evidence at level of significance α=0.05 that the population mean test grade differs among the three learning methods.
NOW YOU CAN DO
Exercises 5–10.