EXAMPLE 5 Performing one-way ANOVA using technology
Researchers from the Institute for Behavioral Genetics at the University of Colorado investigated the effect that the enzyme protein kinase C (PKC) has on anxiety in mice. The genotype for a particular gene in a mouse (or a human) consists of two alleles (copies) of each chromosome, one each from the father and mother. The investigators in the study separated the mice into three groups. In Group 0, neither of the mice's alleles for PKC produced the enzyme. In Group 1, one of the two alleles for PKC produced the enzyme and the other did not. In Group 2, both PKC alleles produced the enzyme. To measure the anxiety in the mice, scientists measured the time (in seconds) the mice spent in the “open-ended” sections of an elevated maze. It was surmised that mice spending more time in open-ended sections exhibit decreased anxiety. The data are provided in Table 5. Use technology to test, at , whether the population mean time spent in the open-ended sections of the maze was the same for all three groups.
675
micemaze
| Group 0 | Group 1 | Group 2 | |||
|---|---|---|---|---|---|
| 15.8 | 14.4 | 5.2 | 7.6 | 10.6 | 9.2 |
| 16.5 | 25.7 | 8.7 | 10.4 | 6.4 | 14.5 |
| 37.7 | 26.9 | 0.0 | 7.7 | 2.7 | 11.1 |
| 28.7 | 21.7 | 22.2 | 13.4 | 11.8 | 3.5 |
| 5.8 | 15.2 | 5.5 | 2.2 | 0.4 | 8.0 |
| 13.7 | 26.5 | 8.4 | 9.5 | 13.9 | 20.7 |
| 19.2 | 20.5 | 17.2 | 0.0 | 0.0 | 0.0 |
| 2.5 | 11.9 | 16.5 | |||
What Result Might We Expect?
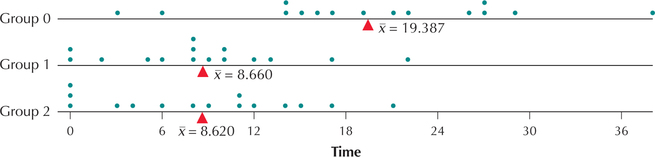
Figure 9 shows a plot of the time in open-ended sections for the mice in the three groups. Note that the Group 1 and Group 2 mice spent on average about the same amount of time in the open-ended sections but that Group 0 spent on average somewhat more time in the open-ended sections. This would tend to suggest that the null hypothesis that all three population means are equal should be rejected. Remember that to reject , it is sufficient for just one of the population means to be different.
Solution
We use the instructions provided in the Step-by-Step Technology Guide at the end of this section (page 679). We frst verify whether the requirements are met.
- The normal probability plots in Figure 10 indicate acceptable normality.
The group standard deviations are , , and . Thus, the largest standard deviation is not greater than twice the smaller, which verifies the equal variances requirement.
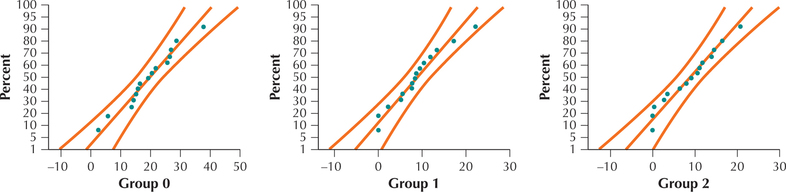Figure 12.10: FIGURE 10 Normal probability plots.676
- The selection of a mouse to a particular group did not affect the selection of mice to the other groups, so that the samples are independent.
Thus, we proceed with the one-way ANOVA.
where the represent the population mean time spent in the open-ended sections of the maze for each group.
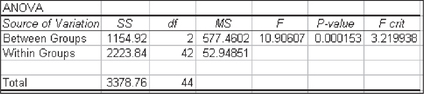
Figure 11 contains the results from the TI-83/84, showing where each statistic corresponds to the ANOVA table structure in Table 3. We have , with a -value of "1.5320224E4" = 0.00015320224. This -value is less than , so we reject . There is evidence at level of significance that the population mean times in the open-ended sections of the maze are not equal for all three groups.
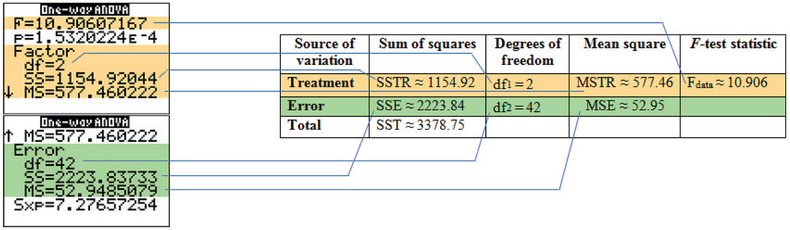
Figure 12 contains the Excel ANOVA results, Figure 13 contains the Minitab ANOVA results, and Figure 14 contains the JMP ANOVA results. Values differ slightly due to rounding.
