Example 6

EXAMPLE 6 Performing one-way ANOVA using the critical-value method

micemaze

Use the data from Example 5 to test, using the critical-value method and level of significance $α = 0.01$ , whether the population mean time spent in the open-ended sections of the maze was the same for all three groups.

Solution

The conditions for performing ANOVA were verified in Example 5.

Step 1 State the hypotheses.

$\begin{matrix} H_{0} : μ_{Group 0} = μ_{Group 1} = μ_{Group 2} \\ H_{a} : not all the population means are equal \end{matrix}$

where the $μ's$ represent the population mean time spent in the open-ended sections of the maze for each group.
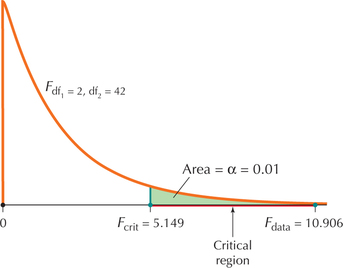
Step 2 Find the critical value $F_{crit}$ and state the rejection rule. The one-way ANOVA test is a right-tailed test, so the $F$ -critical value $F_{crit}$ is the value of the $F$ distribution for ${df}_{1} = k - 1$ and ${df}_{2} = n_{t} - k$ that has area $α$ to the right of it (see Figure 16). Here, ${df}_{1} = 3 - 1 = 2$ and ${df}_{2} = 45 - 3 = 42$ . To find $F_{crit}$ , we may use the F tables or technology. To find our $F_{crit}$ using Excel, enter = FINV(0.01,2,42) in cell A1, as shown in Figure 15. Thus, $F_{crit} = 5.149$ . ANOVA is a right-tailed test, so we will reject $H_{0}$ if $F_{data} ≥ 5.149$ .

FIGURE 15 Using Excel to find the $F$ critical value.
Step 3 Calculate $F_{data}$ . From Example 5, we have $F_{data} = 10.906$ .
Step 4 State the conclusion and interpretation. Because $F_{data} = 10.906 \geq F_{crit} = 5.149$ (Figure 16), we reject $H_{0}$ . There is evidence that not all population mean times spent in the open-ended sections of the maze are equal.

FIGURE 16 $F_{crit} = 5.149$ has area of $α = 0.01$ to the right of it.

NOW YOU CAN DO

Exercises 29–30.