Example 3

EXAMPLE 3 Calculating $t_{data}$

Use the following steps to calculate the test statistic $t_{data} = \frac{b_{1}}{s / \sqrt{\sum {(x - \bar{x})}^{2}}}$ for the data in Table 2:

Find $b_{1}$ , the slope of the regression line.
Calculate $s$ , the standard error of the estimate.
Compute $\sqrt{\sum {(x - \bar{x})}^{2}}$ , the numerator of the sample variance of the $x$ data.

Page 722

Solution

All calculations up to the final result are expressed to nine decimal places.

From Example 1, the slope of the regression line is $b_{1} = - 1.5$ .

Recall from Section 4.3 (page 228) that

$s = \sqrt{\frac{SSE}{n - 2}} = \sqrt{\frac{\sum {(y - \hat{y})}^{2}}{n - 2}} = \sqrt{\frac{\sum {(residual)}^{2}}{n - 2}}$

is the standard error of the estimate. Squaring each residual from Table 2 gives us the squared residuals in Table 3, and the sum of squared residuals, or sum of squares error, equal to

$SSE = {\sum (y - \hat{y})}^{2} = 46.4$

Then the standard error of the estimate is

$s = \sqrt{\frac{SSE}{n - 2}} = \sqrt{\frac{46.4}{8}} \approx 2.408318916.$

Table 13.4: Table 3 Calculating SSE

Residuals $y - \hat{y}$	Squared residuals ${(y - \hat{y})}^{2}$
1.4	1.96
−1.6	2.56
−0.6	0.36
3.4	11.56
−2.6	6.76
−2.6	6.76
3.4	11.56
−0.6	0.36
−1.6	2.56
1.4	1.96
	$Sum = 46.4$

To compute $\sum {(x - \bar{x})}^{2}$ , we note from page 110 in Chapter 3 that the sample variance of $x$ is

$s_{x}^{2} = \frac{\sum {(x - \bar{x})}^{2}}{n - 1}$

Multiplying each side of the equation by $n - 1$ , we obtain an equation for the quantity $\sum {(x - \bar{x})}^{2}$ :

$\sum {(x - \bar{x})}^{2} = (n - 1) \cdot s_{x}^{2}$

The TI-83/84 output from Figure 7 shows that $s_{x} = 6.055300708$ , and, because $n = 10$ ,

$\sum {(x - \bar{x})}^{2} = (n - 1) \cdot s_{x}^{2} = (9) {(6.055300708)}^{2} = 330$

Therefore,

$t_{data} = \frac{b_{1}}{s / \sqrt{\sum {(x - \bar{x})}^{2}}} = \frac{- 1.5}{2.408318916 / \sqrt{330}} \approx - 11.3$

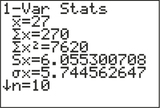FIGURE 7 Summary statistics for the $x$ (age) data.