Example 5

EXAMPLE 5 Hypothesis test for the slope $β_{1}$ using the $p$ -value method and technology

shortmemory

Table 13.5: Table 4

Time $(x)$	Score $(y)$
1	9
1	10
2	11
3	12
3	13
4	14
5	19
6	17
7	21
8	24

In Section 4.3, we considered a study on short-term memory. Ten subjects were given a set of nonsense words to memorize within a certain amount of time and were later scored on the number of words they could remember. The results are repeated here in Table 4. Use the $p$ -value method and technology to test, using level of significance $α = 0.01$ , whether a linear relationship exists between time and score.

Solution

We begin by verifying the regression assumptions. The scatterplot of the residuals versus the fitted values in Figure 8 shows no strong evidence that the independence assumption, the constant variance assumption, or the zero-mean assumption is violated. Also, the normal probability plot of the residuals in Figure 9 offers evidence of the normality of the results. Therefore, we conclude that the regression assumptions are verified, and proceed with the hypothesis test.

Step 1 State the hypotheses and the rejection rule.
- $H_{0} : β_{1} = 0$ No linear relationship exists between time and score.
- $H_{a} : β_{1} \neq 0$ A linear relationship exists between time and score.
Page 724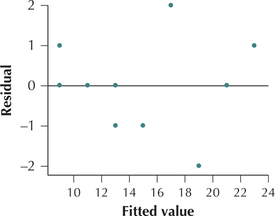

FIGURE 8 Residuals versus fitted values plot.

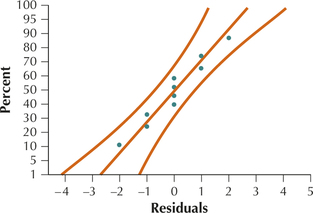FIGURE 9 Normal probability plot of the residuals.

The rejection rule is: reject $H_{0}$ if the $p -value \leq 0.01$ .
Step 2 Calculate $t_{data}$ .

$t_{data} = \frac{b_{1}}{s / \sqrt{\sum {(x - \bar{x})}^{2}}}$

From page 226 in Section 4.3, we have $b_{1} = 2$ . From Example 13 in Chapter 4 on page 228, we have

$s = \sqrt{\frac{12}{8}} \approx 1.224744871$

From the TI-83/84 summary statistics, we have the standard deviation of the $x$ (time) data to be $s_{x} = 2.449489743$ . Thus, using the relationship we learned in Example 3:

$\sum {(x - \bar{x})}^{2} = (n - 1) \cdot s_{x}^{2} = (9) {2.449489743}^{2} = 54$

Therefore,

$t_{data} = \frac{b_{1}}{s / \sqrt{\sum {(x - \bar{x})}^{2}}} \approx \frac{2}{1.224744871 / \sqrt{54}} = 12$

TI-83/84 summary statistics for $x$ (time) data.
Step 3 Find the $p$ -value. For instructions, see the Step-by-Step Technology Guide on page 730. The regression results (including the $p$ -value) for the TI-83/84, Excel, Minitab, and CrunchIt! are shown in Figures 10, 11, 12, and 13. (Differing results are due to rounding.)

FIGURE 10 TI-83/84 regression results.

Page 725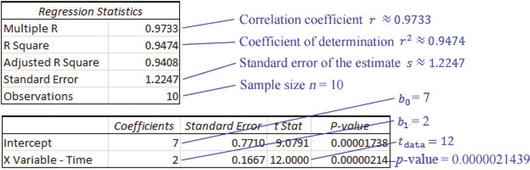

FIGURE 11 Excel regression result.

FIGURE 12 Minitab regression results.

FIGURE 13 Crunchit! regression results.
Step 4 The $p$ -value of about $0.000 is \leq α = 0.01$ , so we reject $H_{0}$ . Evidence exists, at level of significance $α = 0.01$ , for a linear relationship between time and score.

NOW YOU CAN DO

Exercises 19–22.