Example 11

EXAMPLE 11 Wilcoxon signed rank test for a single population median: small-sample case

The Web site www.missingkids.com provides a searchable database of missing children. The ages of the following six children were obtained from this database.

Child	Adam	Juan	Benjamin	Samantha	Kayleen	Aiko
Age	4	9	5	7	6	3

Test, using level of significance $α = 0.10$ , whether the population median age of the missing children equals 6 years old.

Page 14-24

Solution

Step 1 State the hypotheses. We have a two-tailed test:

$\begin{matrix} H_{0} : M = 6 & versus & H_{α} : M \neq 6 \end{matrix}$

where $M$ represents the population median age of the missing children. Thus, the hypothesized value for the median is $M_{0} = 6$ .
Step 2 Find the critical value and state the rejection rule. To find the critical value, we use Appendix Table J, excerpted here in Figure 13. We have a two-tailed test, with level of significance $α = 0.10$ and $n = 5$ , which gives us $T_{crit} = 1$ . The rejection rule is to reject $H_{0}$ if $T_{data} \leq 1$ .

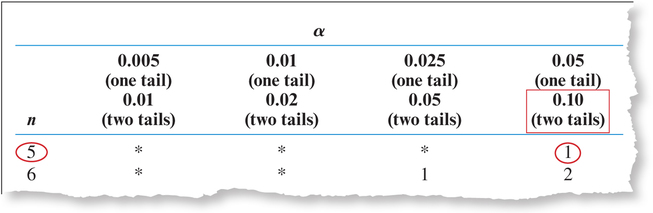FIGURE 13 Using Appendix Table J to find the critical value $T_{crit}$ .

Step 3 Find the value of the test statistic. The calculations to find the signed ranks are shown in Table 11.

Table 14.31: Table 11 Finding the signed ranks for the child age data

Child	Age	$Age - M_{0} = d$	$\| d \|$	Rank of $\| d \|$	Signed rank
Adam	4	$4 - 6 = - 2$	2	3	−3
Juan	9	$9 - 6 = 3$	3	4.5	4.5
Benjamin	5	$5 - 6 = - 1$	1	1.5	−1.5
Samantha	7	$7 - 6 = 1$	1	1.5	1.5
Kayleen	6	$6 - 6 = 0$	—	—	—
Aiko	3	$3 - 6 = - 3$	3	4.5	−4.5

Find $d = age - M_{0} = age - 6$ for each child. Note that the value of $d$ for Kayleen is zero, so we omit Kayleen's age from further calculations.
The absolute values of the differences $| d |$ are shown in the fourth column of Table 11.
We rank the absolute differences. Notice that the absolute values for Benjamin and Samantha are $| d | = 1$ . Had they not been tied, their ranks would have been 1 and 2. The mean of 1 and 2 is $(1 + 2) / 2 = 1.5$ . Thus, each child's age is assigned the rank of 1.5. There is also a tie between Juan and Aiko, with $| d | = 3$ . Had they not been tied, their ranks would have been 4 and 5, so each child's age is assigned the mean rank of 4.5. The ranks of the absolute differences $| d |$ are shown in the fifth column of Table 11.
Attach to each rank the sign of its corresponding value of $d$ . This is its signed rank. For example, the rank of $| d |$ for Adam is 3, but the sign of $d = - 2$ for Adam is negative (–). We attach this negative sign to the rank for Adam to give us Adam's signed rank of –3. Replace each original data value with its corresponding signed rank, shown in the last column of Table 11.

Page 14-25

Next, we need to sum the positive ranks and the negative ranks. There are two positive signed ranks: Juan's 4.5 and Samantha's 1.5. Thus, $T_{+} = 4.5 + 1.5 = 6$ . There are three negative signed ranks, which we add to get $T_{-} : - 3 + (- 1.5) + (- 4.5) = - 9$ . Taking the absolute value gives us $| T_{-} | = | - 9 | = 9$ . Table 9 tells us that $T_{data} = the smaller of T_{+} and | T_{-} |$ Thus, $T_{data} = 6$ .

Step 4 State the conclusion and the interpretation. The rejection rule is to reject $H_{0}$ if $T_{data} ≤ 1$ . Because $T_{data} = 6$ is not ≤1, we do not reject $H_{0}$ . There is insufficient evidence that the population median age of missing children differs from 6 years old.

NOW YOU CAN DO

Exercises 19–22.