EXAMPLE 4 Large-sample sign test for the population median using technology

nutrition

The data set Nutrition (on the text website) contains information about 961 food items. The variable calories states the number of calories per serving for each food item. Consider these 961 food items to be a random sample of the population of all food items. Test whether the population median number of calories differs from 120, using level of significance .

Solution

The 961 food items are a random sample from the population of all food items, so the conditions for performing the sign test for the population median are met.

  • Step 1 State the hypotheses. The key words “differs from” indicate that we have a two-tailed test. The answer to the question “Differs from what?” gives us the value of .

    where represents the population median calories per food item.

  • Step 2 Find the critical value and state the rejection rule. We have a large sample here. Among the 961 values, there are 18 that are equal to the proposed population median . We ignore values that do not have a sign associated with them, so . We are given the level of significance , so our . We will reject if .

  • Step 3 Find the value of the test statistic. We use the instructions provided in the Step-by-Step Technology Guide at the end of this section. Figure 3 shows the Minitab results from the sign test for the population median. The value for “Below” is the number of minus signs, and the value for “Above” is the number of plus signs. So, we have 448 minus signs and 495 plus signs. Thus, the sample size is . From Table 3, , whichever is smaller. Thus, . We then calculate the test statistic :

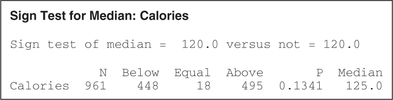    image
    Figure 14.3: FIGURE 3 Minitab output for the sign test for the population median.

    image The value of reported by Minitab does not equal the actual sample size used for the sign test. To find , we need to subtract the number of data values equal to .

    14-10

  • Step 4 State the conclusion and the interpretation. Because is not , we do not reject . The evidence is insufficient that the population median number of calories differs from 120 calories per serving. The Minitab output shows that the sample median equals 125 calories, which is a little bit different from , but the difference is not statistically significant.

NOW YOU CAN DO

Exercises 17–20.