EXAMPLE 17Finding probabilities using the binomial table

Use the binomial table and the binomial distribution from Example 16 to find the following probabilities:

  1. No Americans are sleep-deprived.
  2. At least one American is sleep-deprived.

Solution

  1. From Example 16, we have a binomial distribution with and . We next find and in the binomial table. In Figure 8:
    • Look under the column until you find . That is the portion of the table you will use.
    • Then go across the top of the table until you get to .
    • For part (a), , so go down the column until you see 0 under the column on the left (and in the subgroup with ).
    • The number in the column is 0.4096 (see Figure 8), which is the same answer we calculated in Example 16(a).
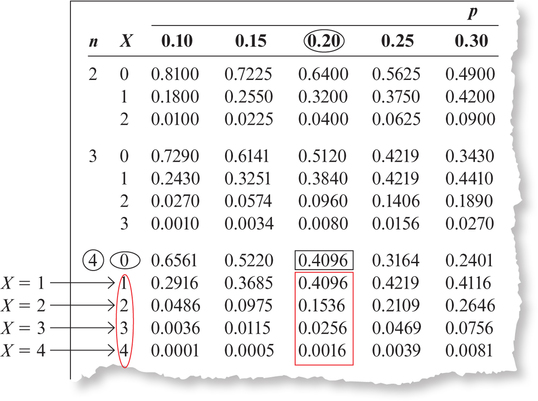      image
      Figure 6.10: FIGURE 8 Excerpt from the binomial tables.
  2. In this case, “at least 1” means 1 or 2 or 3 or 4. So, by the Addition Rule for Mutually Exclusive Events, find the probabilities for , , , and , and add them up. Using the same column with column head 0.20 in the table as in part (a), we add up the four probabilities.

This is the same answer we calculated in Example 16(b), but it is arrived at in a different way.