EXAMPLE 22Finding probabilities using the Poisson distribution

A study was done of the number of cardiac arrests to occur per week in a particular hospital of 850 beds over a period of 5 years.4 The number of cardiac arrests fulflls the requirements for the Poisson probability distribution and has a mean of cardiac arrests per week. Calculate the following probabilities:

  1. The probability of two cardiac arrests in a given week
  2. The probability of fewer than two cardiac arrests in a week
  3. The probability of at most two cardiac arrests in a week
  4. The probability of more than two cardiac arrests in a week
  5. The probability of at least three cardiac arrests in a week

Solution

The number of cardiac arrests fulfills the requirements for the Poisson probability distribution, so we may use the Poisson probability distribution formula to calculate the desired probabilities. To use this formula, we must determine the values of and . For each of (a)–(e), we have . The Poisson distribution with for is shown in Figure 18.

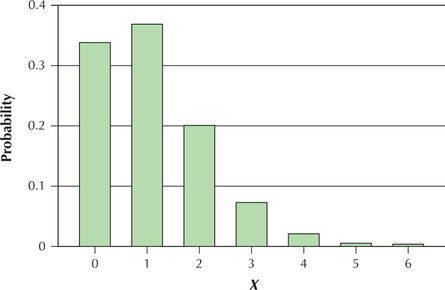
image
Figure 6.20: FIGURE 18 The Poisson distribution for . (Note that there is no upper limit to the value that may take, but that the probabilities for are very small.)

  1. Here, , so the probability that is

  2. The Poisson distribution is a discrete distribution, so that “fewer than 2” means or . We thus find and , and add the resulting probabilities to arrive at the answer.

    So the probability of fewer than two cardiac arrests in a week equals .

  3. The phrase “at most 2” means or or . We thus find , , and and add the resulting probabilities to arrive at the answer. We have already found and from part (b) and have found from part (a). Thus, the probability of, at most, two cardiac arrests in a week equals

    344

  4. The phrase “more than 2” means , , and so on to infinity. In Figure 18, these probabilities are represented by the rectangles for , , and so on. Now the Law of Total Probability says that the sum of the probabilities of all values of equals 1. Thus, the probabilities represented by the rectangles for , , and so on equals 1 minus the sum of the rectangles for , , and . In other words, — . We found in part (c). Thus, .
  5. The phrase “at least 3” means , , and so on to infinity. These are the same -values represented in part (d) by the phrase “more than 2.” Thus, .

NOW YOU CAN DO

Exercises 9–14.