EXAMPLE 33Finding the -value with given area to its left
Recall that the th percentile is the value in the data set such that percent of the data values fall at or below that value. Thus, represents the 90th percentile of the distribution because it is greater than 90% of -values.
Find the -value with area 0.90 to its left.
Solution
- Step 1 Draw the standard normal curve. Label the .
- Step 2 Shade the area to the left of . Remember that we are given an area and are looking for a value of . Label the area to the left of with the given area (0.90), as shown in Figure 37.
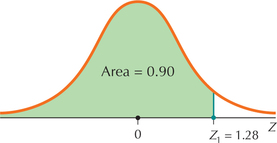 Figure 6.39: FIGURE 37 is the value of with area 0.90 to the left of it.
Figure 6.39: FIGURE 37 is the value of with area 0.90 to the left of it. - Step 3 Look for 0.90 on the inside of the table (that is, in the body of the table), because the values inside the table represent areas. Because there is no 0.90 inside the table, by convention we take the area that is closest to 0.90, which is 0.8997. Next is the trick of the backward problems and the reason for that name. Move from 0.8997 to the left until you reach 1.2 in the first column, and then move up from 0.8997 until you get to 0.08 (see Figure 38). Putting these values together, we get .
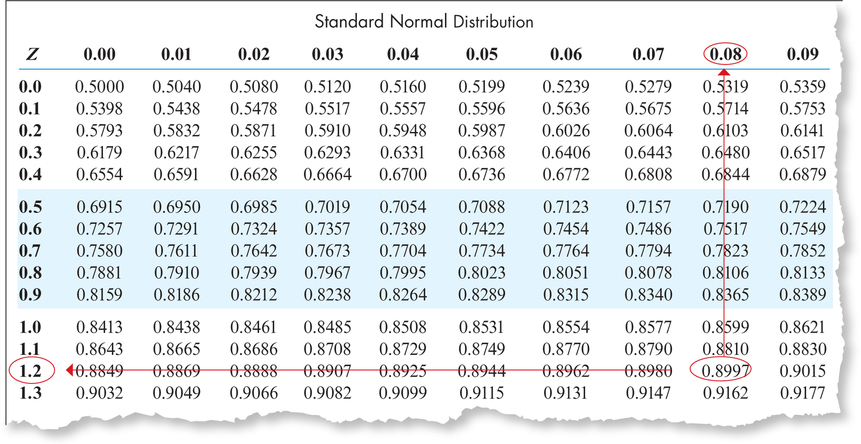 Figure 6.40: FIGURE 38 Using the table to find a value of for a given area.
Figure 6.40: FIGURE 38 Using the table to find a value of for a given area.
NOW YOU CAN DO
Exercises 71–78.