EXAMPLE 38Finding probability for a normal random variable

image

image SAT Scores and AP Exam Scores

The College Board reports that the population mean Math SAT score in 2013 was = 514, with a population standard deviation of , and that the scores follow a normal distribution. Suppose that a local college wants to identify at-risk math students, which it considers to be students scoring below 396 on the Math SAT Find the proportion of students who score below 396 on the Math SAT.

Remember that you may solve problems asking for proportions or percentages by finding the appropriate probability.

Solution

  • Step 1 Determine , , and .

    We are given that the normal random variable = Math SAT score has mean and standard deviation . In the center of the number line, mark the mean . Also mark on the number line the value of about which the problem is asking. Figure 48 shows the graph of (the Math SAT scores) with the mean of 514 and the score of 396 marked.

    You need to know the proportion of scores below 396, so shade the area under the curve to the left of 396. We can express this proportion as a probability, the probability that a randomly chosen student will score less than 396, or . Just by looking at Figure 48, you should be able to get a rough idea of what the proportion of these scores will be. Certainly, this proportion will be less than 50%. If you get an answer such as “60%” for your proportion, you should recognize that it is wrong.

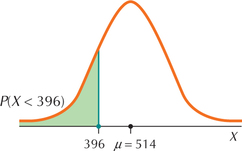    image
    Figure 6.50: FIGURE 48 Graph of proportion of Math SAT scores lower than 396.

  • Step 2 Standardize.

    Now standardize the random variable to the standard normal :

    Find the -value corresponding to the Math SAT score of 396:

    So the -value associated with a score of 396 is −1, which indicates that the score of 396 is 1 standard deviation below the mean of 514.

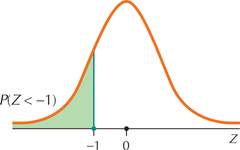    image
    Figure 6.51: FIGURE 49 Graph of .

  • Step 3 Draw the standard normal curve.

    Scores less than 396 are more than 1 standard deviation below the mean, so shade the area to the left of −1 in Figure 49. Now find the area to the left of using the methods of Section 6.4.

    Step 4 Find the area under the standard normal curve.

    The table tells us that the area to the left of is 0.1587.

    The proportion of scores below 396 is 0.1587, or 15.87%. Note that this value for agrees with our earlier intuition that the proportion was less than 50%.

NOW YOU CAN DO

Exercises 3–9.