EXAMPLE 14 Finding probabilities Using the Central Limit Theorem for Proportions

Using the information in Example 13, find the probability that a sample of vehicles will have a proportion of large trucks greater than 9% for samples of size (a) 30 vehicles and (b) 117 vehicles.

Solution

  1. We found in Example 13(a) that this sample size of does not meet the minimum sample size required for the sampling distribution of to be approximately normal, so we cannot conclude that the sampling distribution of is approximately normal. Thus, we cannot solve this problem.

  2. From Example 13(b), the sampling distribution of is approximately normal with mean and standard deviation . We are then faced with a normal probability problem similar to those in Section 6.5. Figure 14 shows the sampling distribution of and the probability we are interested in, . Using Fact 8, we standardize as follows:

    Thus, , as shown in Figure 15.

Again, we can use our normal distribution methods from Section 6.5 because the Central Limit Theorem for Proportions gives us approximate normality.

420

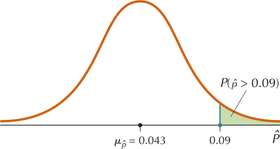
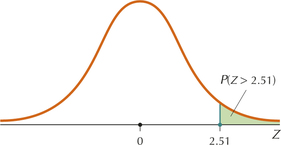
image
Figure 7.13: FIGURE 14 Area to the right of equals …
image
Figure 7.14: FIGURE 15 Area to the right of .

Following Table 8 in Chapter 6 (page 355), we look up in the table and subtract this table area (0.9940) from 1 to get the desired tail area. That is,

So the probability that the sample proportion of large trucks will exceed 0.09 is 0.006.

NOW YOU CAN DO

Exercises 25–32.