EXAMPLE 5 Finding probabilities for the sample mean: Comparing with
Suppose the number of “likes” for Facebook pages is normally distributed with mean 70 likes and standard deviation 10 likes.
- Find the probability that a randomly chosen Facebook user likes more than 80 pages.
- Suppose we take many samples of size Facebook users. Describe the sampling distribution of the sample mean.
- Find the probability that a sample of 25 Facebook users will have a mean number of page likes greater than 80.
Solution
This is a normal probability problem, which we learned how to do in Section 6.5
403
using Case 2 from Table 8 in Chapter 6 (page 355), which shows how to find area to the right of a Z-value. Therefore, a 15.87% probability exists that a randomly chosen student will like more than 80 Facebook pages (Figure 5a).
It is especially important when answering sampling distribution problems to draw graphs of the original distribution of and the sampling distribution of . Always draw graphs when solving probability problems. They bring in the “artistic side” of your brain to help the “analytic side” solve the problem.
We are given and . So, by Fact 1, . And by Fact 2,
Next, we are given that the population of Facebook likes is normal. Therefore, by Fact 3, the sampling distribution of is distributed as normal (70, 2) (see Figure 5b). This represents Case 1 from the Three Cases above.
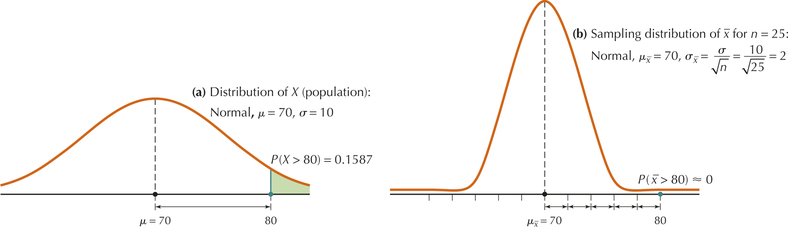 Figure 7.5: FIGURE 5 Distribution of and sampling distribution of for Example 5.
Figure 7.5: FIGURE 5 Distribution of and sampling distribution of for Example 5.- Once we know that the sample mean is normally distributed, we can standardize the sample mean number of page likes, as we have for other normal random variables. Just be sure to use , the standard error of the mean, and not , the standard deviation for the population. is always smaller.
Applying Fact 4,
We need to standardize the value of 80 page likes, too.
Thus,
as shown in Figure 5b. Because is standard normal, nearly all observations lie between −3 and 3. Thus, the table does not go up to 5 because the probabilities are so close to 0. The TI-83 provides the more precise probability of , or about 3 in 10 million.
NOW YOU CAN DO
Exercises 27–32.