EXAMPLE 6 Finding a value of , given a probability or area

Use the information in Example 5 to do the following:

  1. Find the 95th percentile of the sample mean number of Facebook page likes from samples of size .
  2. Find the 5th percentile of the sample means.
  3. What two symmetric values for the sample mean contain the middle 90% of all sample means between them?
  4. Verify that .

Solution

The 95th percentile of the sample mean number of Facebook likes is the value of with area 0.95 to the left of it.

  1. We want the 95th percentile, so we seek 0.95 on the inside of the table. Because 0.95 is not in the table, we take the closest value. The two closest values, 0.9495 and 0.9505, are equally close, so we split the difference. Working backward from 0.9495, we find , and for 0.9505 we find . Splitting the difference, we get . This value of is the 95th percentile of the standard normal distribution.

    Because we are looking for a sample mean number of page likes, 1.645 is probably not the answer. We need to “unstandardize” by transforming this value of to an -value:

    Thus, the 95th percentile of the sample means for the number of Facebook page likes is 73.29.

  2. The sampling distribution is normal, so it is also symmetric. Thus, the 95th percentile and the 5th percentile are the same distance away from the mean. Because the 95th percentile is above the mean, the 5th percentile must be 3.29 below the mean, or .

  3. This is just another way of asking for the 5th and 95th percentiles, which we found in parts (a) and (b). (See Figure 6.) The answer is 66.71 and 73.29.

    405

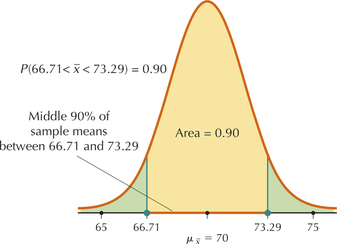    image
    Figure 7.6: FIGURE 6 Middle 90% of the sample means.

  4. We seek , as shown in Figure 6. Proceeding with the calculations, we have, as expected,

NOW YOU CAN DO

Exercises 33–58.