Example 23

EXAMPLE 23 Finding the critical values

Note: If the appropriate degrees of freedom are not given in the table, the conservative solution is to take the next row with the smaller df.

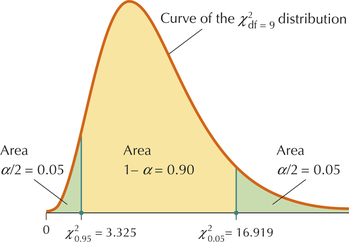
Find critical values for a 90% confidence interval, where we have a sample size of size .

Solution

For a 90% confidence interval,

So we are seeking (1) , the critical value with area to the right of it, and (2) , the critical value with area to the right of it.

Because , the degrees of freedom is . To find for df = 9, go across the top of the table (Table E in the Appendix) until you see 0.95 (Figure 36). is somewhere in that column. Now go down that column until you see your number of degrees of freedom df = 9. Thus, for df = 9, . For a distribution with 9 degrees of freedom, there is area = 0.95 to the right of 3.325.

Figure 8.36: FIGURE 36 Finding and using the table.

476

Similarly, is found in the column labeled “0.05” and the row corresponding to . We find that , as shown in Figure 37.

Figure 8.37: FIGURE 37 critical values for the distribution with df = 9.

NOW YOU CAN DO

Exercises 9–16.