EXAMPLE 5 Constructing a interval for the population mean for a large sample size

image

image Motor Vehicle Fuel Efficiency

One of the variables in our case study is City MPG, which is the number of miles a vehicle can travel in city conditions on one gallon of gas. Because we have information on the entire population of 1141 vehicles, we know the population standard deviation . We obtained a sample of 100 vehicles and observed a sample mean city gas mileage of .

  1. Determine whether the requirements are met for constructing the interval for .
  2. Construct a 90% confidence interval for , the population mean City MPG for all vehicles.
  3. Interpret the confidence interval.

Note: As a check on your arithmetic, make sure that .

In other words, the sample mean should lie exactly midway between the lower bound and the upper bound.

Solution

  1. We are not given any information about the distribution of the population, so we don't know if the population is normally distributed. However, the sample size is greater than 30, and the value of is known; therefore, we can proceed to construct the confidence interval.

  2. The formula for the confidence interval is given by

    We are given , , and . For a confidence level of 90%, Table 1 provides the value of . Plugging into the formula:

  3. We are 90% confident that , the population mean City MPG for all motor vehicles, lies between 19.78 mpg and 21.64 mpg. (See Figure 2.)
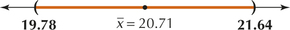    image
    Figure 8.2: FIGURE 2 90% confidence interval for the population mean City MPG.

NOW YOU CAN DO

Exercises 31–34.