Example 6

EXAMPLE 6 $Z$ intervals for $μ$ using technology

highwaympg16

Motor Vehicle Fuel Efficiency

Another of the variables in our case study is Highway MPG, which is the number of miles a vehicle can travel on a highway on one gallon of gas. We know the population standard deviation $σ = 6.326 mpg$ . The sample of 16 vehicles, shown here, has a sample mean highway gas mileage of $\bar{x} = 26.94 mpg$ .

Vehicle	Highway MPG	Vehicle	Highway MPG
Honda CR-V	30	Subaru Impreza	25
Nissan Pathfinder	26	Ford Mustang	26
Acura MDX	28	Cadillac ATS	31
Porsche Cayenne	29	Chevrolet Camaro	24
Mercedes-Benz GLK 250	33	Ford Taurus	29
Chevrolet Chevy SS	21	Ford Expedition	20
Dodge Charger	27	Lincoln MKT	25
Jeep Compass	23	BMW X1	34

Determine whether the $Z$ interval for $μ$ may be applied.
Use the TI-83/84, Minitab, and JMP to construct a 95% $Z$ confidence interval for the population mean Highway MPG.

Solution

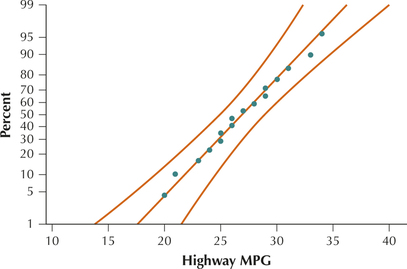
The sample size $n = 16$ is not large $(\geq 30)$ , so we need to check if the data follow a normal distribution. The normal probability plot of the data in Figure 4 supports the assumption of normality. Further, the population standard deviation is known. We may thus apply the $n$ interval for $μ$ .

FIGURE 4 Normal probability plot of the Highway MPG data.
We shall use the instructions provided in the Step-by-Step Technology Guide at the end of this section (page 441). The results for the TI-83/84 in Figure 5 show that the 95% $Z$ confidence interval for the population mean Highway MPG is

$lower bound = 23.838, upper bound = 30.037$

Figure 5 also shows the sample mean $\bar{x} = 26.9375$ , the sample standard deviation $σ = 3.991136012$ , and the sample size $n = 16$ .

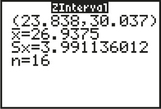FIGURE 5 TI-83/84 results.

The Minitab results are provided in Figure 6. The “assumed standard deviation” is indicated to be $σ = 6.326$ . Then the sample size $n = 16$ , the sample mean $\bar{x} = 26.94$ , and the sample standard deviation $s = 3.99$ are displayed. “SE Mean” refers to the standard error of the mean, but we don't need it here. Finally, the 95% confidence interval is given as (lower bound = 23.84, upper bound = 30.04).

Page 437

FIGURE 6 Minitab results.

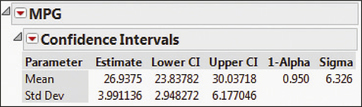
The JMP results are shown in Figure 7. The sample mean $\bar{x} = 26.9375$ is shown in the first column, with the sample standard deviation $s = 3.991136$ below it. The 95% confidence interval is given in the row labeled Mean, with lower bound = 23.84 (rounded) and upper bound = 30.04 (rounded).

FIGURE 7 JMP results.