EXAMPLE 10 Test for , critical-value method, left-tailed test

For the hypotheses in Example 8, perform the test for the population mean, using level of significance . Assume systolic blood pressure is normally distributed.

Solution

We may use the test, because the population of systolic blood pressure readings is normally distributed, and the population standard deviation σ is known.

  • Step 1 State the hypotheses.

    From Example 8, we have

    where represents the population mean systolic blood pressure reading.

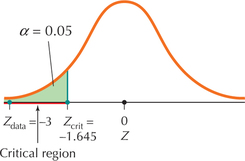    image
    Figure 9.4: FIGURE 4 Critical region for a left-tailed test.

  • Step 2 Find and state the rejection rule.

    Example 8 gives us the critical value , and Table 4 tells us that, for level of significance , we will reject if , that is, if (Figure 4).

  • Step 3 Calculate .

    From page 499, we know that

  • Step 4 State the conclusion and the interpretation.

    In Step 2, we stated that we would reject if . Our of , therefore, we reject . Our interpretation is: “There is evidence at level of significance that the population mean systolic blood pressure reading is less than 110.”

NOW YOU CAN DO

Exercises 41–44.