Example 13

EXAMPLE 13 The $Z$ test for the mean using the $p$ -value method: One-tailed test

FlightStats.com compiles user ratings for airports worldwide. The mean rating for JFK International Airport in New York for July 2014 was 3.0 (out of 5). Assume that the population standard deviation of user ratings is known to be $σ = 1$ . A random sample taken this year of $n = 36$ user ratings for JFK Airport showed a mean of $\bar{x} = 2.75$ . Using level of significance $α = 0.05$ , test whether the population mean user rating for JFK Airport has fallen since 2014.

Solution

The sample size $n = 36$ is large, and the population standard deviation $σ$ is known. We may therefore perform the $Z$ test for the mean.

Step 1 State the hypotheses and the rejection rule.

The key words here are “has fallen,” which means “is less than.” The answer to the question “Less than what?” gives us $μ_{0} = 3.0$ . Thus, our hypotheses are

$H_{0} : μ = 3.0 versus H_{a} : μ < 3.0$

where $μ$ refers to the population mean user rating for JFK Airport. We will reject $H_{0}$ if the $p -value \leq α = 0.05$ .
Step 2 Calculate $Z_{data}$ .

We have $\bar{x} = 2.75, μ_{0} = 3.0, n = 36,$ , and $σ = 1$ . Thus, our test statistic is

$Z_{data} = \frac{\bar{x} - μ_{0}}{σ / \sqrt{n}} = \frac{2.75 - 3.0}{1 / \sqrt{36}} = - 1.5$

Page 511
Step 3 Find the $p$ -value.

Our hypotheses represent a left-tailed test from Table 5. Thus,

$p -value = P (Z < Z_{data}) = P (Z < - 1.5)$

This is a Case 1 problem from Table 8 in Chapter 6 (page 355). The $Z$ table (Appendix Table C) provides us with the area to the left of $Z = - 1.5$ (Figure 7):

$P (Z < - 1.5) = 0.0668$

Thus, the $p$ -value is 0.0668.

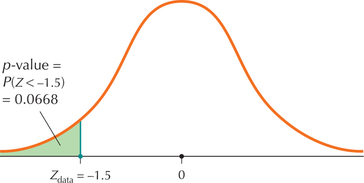FIGURE 7 The $p$ -value 0.0668 is not ≤ 0.05, so do not reject $H_{0}$ .
Step 4 State the conclusion and interpretation.

Our level of significance is $α = 0.05$ (from Step 1). The $p -value = 0.0668$ is not ≤ 0.05, therefore, we do not reject $H_{0}$ . There is insufficient evidence at the level of significance $α = 0.05$ that the population mean user rating for JFK Airport is less than 3.0.

NOW YOU CAN DO

Exercises 21–26.