Example 19

EXAMPLE 19 $t$ Test for $μ$ using critical-value method: two-tailed test

CNN reported in 2014 that, even after factoring in part-time jobs, Americans worked an average of 38 hours per week. Suppose a social science researcher disputes this finding and is interested in testing whether the population mean number of hours worked per week differs from 38. A random sample of $n = 30$ working Americans yields a sample mean of $\bar{x} = 35.26$ hours worked, with a sample standard deviation of $s = 10$ hours. If the conditions are met, perform the appropriate hypothesis test using level of significance $α = 0.10$ .

Solution

Because $n = 30 \geq 30$ , we may proceed with the $t$ test.

Step 1 State the hypotheses.

The key words “differs from” indicate a two-tailed test, with $μ_{0} = 38$ , because we are testing whether $μ$ differs from 38. So our hypotheses are

$\begin{array}{l} H_{0} : μ = 38 & versus & H_{a} : μ \neq 38 \end{array}$

where $μ$ represents the population mean number of hours worked per week.

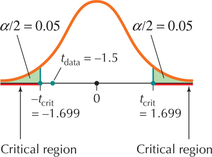FIGURE 21 Critical region for two-tailed test.
Step 2 Find $t_{crit}$ and state the rejection rule.

To find $t_{crit}$ for a two-tailed test with level of significance $α = 0.10$ , we look in the 0.10 column in the “Area in two tails” section of Table D in the Appendix. The degrees of freedom $df = n - 1 = 29$ gives us $t_{crit} = 1.699$ . From Table 8, the rejection rule is: “Reject $H_{0}$ if $t_{data} \geq 1.699$ or $t_{data} \leq - 1.699$ .”

Page 529
Step 3 Calculate $t_{data}$ :

$t_{data} = \frac{\bar{x} - μ_{0}}{s / \sqrt{n}} = \frac{35.26 - 38}{10 / \sqrt{30}} \approx - 1.5$
Step 4 State the conclusion and the interpretation.

$t_{data} = - 1.5$ is not ≥1.699 and it is not ≤−1.699; therefore, we do not reject $H_{0}$ . See Figure 21. There is insufficient evidence, at level of significance $α = 0.10$ , that the population mean number of hours worked per week differs from 38.

NOW YOU CAN DO

Exercises 9–14.