Example 20

EXAMPLE 20 $t$ Test using the $p$ -value method: Right-tailed test

milkprice

The U.S. Bureau of Labor Statistics reports that the mean price for a gallon of milk in July 2014 was $3.65. Gallons of milk were recently bought in a random sample of $n = 10$ different cities, with the prices shown in the accompanying table. Test, using level of significance $α = 0.05$ , whether the population mean price for a gallon of milk is greater than $3.65.

Solution

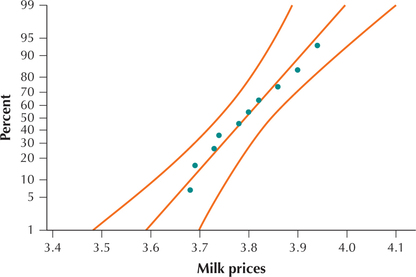
We first check whether the conditions for performing the $t$ test are met. Because our sample size is small, we must check for normality. The normal probability plot in Figure 22 shows acceptable normality, allowing us to proceed with the $t$ test.

FIGURE 22 Normal probability plot of milk prices.

Step 1 State the hypotheses and the rejection rule.

The key words “is greater than” means that we have a right-tailed test. Answering the question “Greater than what?” gives us $μ_{0} = 3.65$ .

$\begin{array}{l} H_{0} : μ = 3.65 & v e r s u s & H_{a} : μ > 3.65 \end{array}$

where $μ$ represents the population mean price of milk. We will reject $H_{0}$ if the $p -value \leq α = 0.10$ .
Step 2 Calculate $t_{data}$ .

We use the instructions from the Step-by-Step Technology Guide on page 537. Figure 23 shows the TI-83/84 results from the $t$ test for $μ$ .

FIGURE 23 TI-83/84 results for right-tailed $t$ test.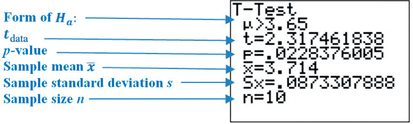

For a more accurate calculation of the $p$ -value, we retain 9 decimal places for the value of $t_{data}$ .

Using the statistics from Figure 23, we have the test statistic

$t_{data} = \frac{\bar{x} - μ_{0}}{s / \sqrt{n}} = \frac{3.714 - 3.65}{0.0873307888 / \sqrt{10}} = 2.317461838 \approx 2.3175$
Step 3 Find the $p$ -value.

From Figures 23 and 24, we have

$p -value = P (t \geq 2 .317461838) = 0 .0228376005 \approx 0.0228$

Page 531

FIGURE 24 The $p$ -value for a right-tailed $t$ tes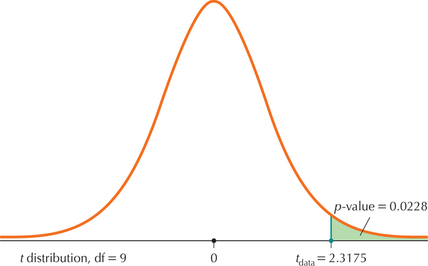t.
Step 4 State the conclusion and the interpretation.

The $p-value \approx 0.0228$ is less than the level of significance $α = 0.05$ ; therefore, reject $H_{0}$ . There is evidence, at level of significance $α = 0.05$ , that the population mean price of milk is greater than $3.65.

NOW YOU CAN DO

Exercises 15–20.