EXAMPLE 22 Estimating the $p$-value using the $t$ table

Suppose we did not have access to technology. Estimate the $p$-value from Example 19 using the $t$ table (Appendix Table D). For Example 19, our hypotheses are

where $\mu$ represents the population mean number of hours worked per week. Our test statistic is $t_{\text{data}}=-1.5$.

Solution

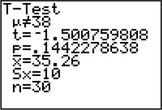
For a two-tailed test, choose the row of the $t$ table with the heading “Area in two tails.” Then select the row in the table with the appropriate degrees of freedom, in this case $\text{df}=n-1=30-1=29$. Note the $t$-values in this row: 1.311, 1.699, 2.045, 2.462, and 2.756. Think of these values as existing on a horizontal number line. We want to place our $t_{\text{data}}=-1.5$ somewhere on this number line, but all the $t$-values in the table are positive. Fortunately, because of the symmetry of the $t$ distribution about zero, we may take $\left|t_{\text{data}}\right|=1.5$. Now, where would $\left|t_{\text{data}}\right|=1.5$ fit on this “number line”? Between 1.311 and 1.699, as indicated in Figure 31, an excerpt from the $t$ table. Therefore, we may estimate the $p$-value to be between 0.20 and 0.10. In fact, the actual $p$-value for this problem is about 0.144 (see Figure 32), so that our estimate is confirmed.