Example 24

EXAMPLE 24 Interpreting software output

Each of (a) and (b) represent software output from a $t$ test for $μ$ . For each, examine the indicated software output, and provide the following steps:

Step 1 State the hypotheses and the rejection rule.
Step 2 Find $t_{data}$ .
Step 3 Find the $p$ -value.
Step 4 State the conclusion and the interpretation.

Use level of significance $α = 0.10$ for each hypothesis test.

SPSS output for a $t$ test for $μ$ , where $μ$ represents the population mean number of orchard farms per county, nationwide.
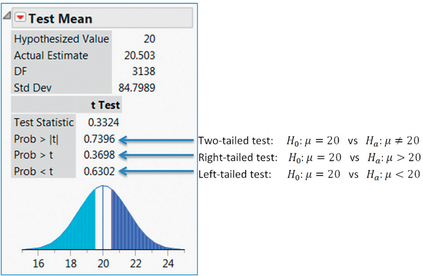
JMP output for a $t$ test for $μ$ , where $μ$ represents the population mean number of grocery stores per county, nationwide.

Page 536

Solution

Interpreting the SPSS output.
- Step 1 State the hypotheses and the rejection rule.
  
  In the SPSS output, the “Test $Value = 40$ ” indicates that $μ_{0} = 40$ . Also, the “2-tailed” in the output indicates that we have a two-tailed test. Thus, our hypotheses are:
  
  $\begin{array}{l} H_{0} : μ = 40 & versus & H_{a} : μ \neq 40 \end{array}$
  
  where $μ$ represents the population mean number of orchard farms per county, nationwide. We will reject $H_{0}$ if the $p$ -value is less than level of significance $α = 0.10$ .
- Step 2 Find $t_{data}$ .
  
  Under the “t” in the SPSS is the value for $t_{data}, - 1.079$ .
- Step 3 Find the $p$ -value.
  
  The abbreviation “Sig.” stands for “Significance,” which represents the $p$ -value: 0.281.
- Step 4 State the conclusion and the interpretation.
  
  The $p$ -value of 0.281 is not less than the level of significance $α = 0.10$ , so we do not reject $H_{0}$ . There is insufficient evidence that the population mean number of orchard farms per county differs from 40.
Interpreting the JMP output.
- Step 1 State the hypotheses and the rejection rule.
  
  In the JMP output, the “Hypothesized Value” indicates that $μ_{0} = 20$ . Now, JMP is unusual in that it performs all three types of hypothesis test simultaneously: two-tailed, right-tailed, and left-tailed, as shown in the JMP output. It does not specify a particular form of the test. Let us use the right-tailed test for this example. Thus, our hypotheses are:
  
  $\begin{array}{l} H_{0} : μ = 20 & vs & H_{a} : μ > 20 \end{array}$
  
  where $μ$ represents the population mean number of grocery stores per county, nationwide. We will reject $H_{0}$ if the $p$ -value is less than level of significance $α = 0.10$ .
- Step 2 Find $t_{data}$ .
  
  Next to “Test Statistic” in the JMP output, we find the value of our test statistic, $t_{data}$ , 0.3324.
- Step 3 Find the $p$ -value.
  
  Here, we need to be careful, because JMP gives us three different $p$ -values, depending on which form of the hypothesis test is performed. We chose the right-tailed test, so our $p$ -value is next to $“ Prob > t ”: p -value = 0.3698$ , as indicated in the JMP output.
- Step 4 State the conclusion and the interpretation.
  
  The $p$ -value of 0.3698 is not less than the level of significance $α = 0.10$ , so we do not reject $H_{0}$ . There is insufficient evidence that the population mean number of grocery stores per county is greater than 20.

NOW YOU CAN DO

Exercises 37–40.