Example 26

EXAMPLE 26 $Z$ test for $p$ using the critical-value method

As a check on your arithmetic, the two quantities you obtain when checking the normality conditions should add up to $n$ . Here, $80 + 320 = 400 = n$ .

Refer to Example 25. Test whether the population proportion of Chromebook computers has changed from 20%, using the critical-value method and level of significance $α = 0.10$ .

Solution

First, we check that both of our normality conditions are met. From Example 25, we have $p_{0} = 0.20$ and $n = 400$ .

$\begin{array}{l} n \cdot p_{0} = (400) (0.20) = 80 \geq 5 & and & n \cdot q_{0} = (400) (0.80) \end{array} = 320 \geq 5$

The normality conditions are met and we may proceed with the hypothesis test.

Step 1 State the hypotheses.

From Example 25, our hypotheses are

$\begin{array}{l} H_{0} : p = 0.20 & versus & H_{a} : p \neq 0.20 \end{array}$

where $p$ represents the population proportion of computers that are Chromebooks.
Step 2 Find $Z_{crit}$ and state the rejection rule.

We have a two-tailed test, with $α = 0.10$ . This gives us our critical value $Z_{crit} = 1.645$ . the rejection rule from Table 11 is: Reject $H_{0}$ if $Z_{data} \geq 1.645$ or $Z_{data} \leq - 1.645$ (Figure 35).

FIGURE 35 $Z_{data}$ does not fall in the critical region.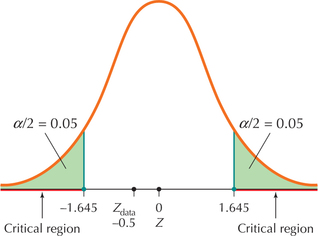
Step 3 Calculate $Z_{data}$ .

From Example 25, we have $Z_{data} = - 0.5$

Page 546
Step 4 State the conclusion and the interpretation.

The test statistic $Z_{data} = - 0.5$ is not $\geq 1.645$ and not $\leq - 1.645$ . Thus, we do not reject $H_{0}$ . There is insufficient evidence at level of significance $α = 0.10$ that the population proportion of computers that are Chromebooks differs from 20%.

NOW YOU CAN DO

Exercises 15–18.