Example 28

EXAMPLE 28 Performing the $Z$ test for $p$ using technology

A study reported that 1% of American Internet users who are married or in a long-term relationship met on a blind date or through a dating service.¹³ A survey of 500 American Internet users who are married or in a long-term relationship found 8 who met on a blind date or through a dating service. If appropriate, test whether the population proportion has increased. Use the $p$ -value method with level of significance $α = 0.05$ .

Solution

We have $p_{0} = 0.01$ and $n = 500$ . Checking the normality conditions, we have

$\begin{array}{l} n \cdot p_{0} = (500) (0.01) = 5 \geq 5 & and & n \cdot q_{0} = (500) (0.99) = 495 \geq 5 \end{array}$

The normality conditions are met and we may proceed with the hypothesis test.

Step 1 State the hypotheses and the rejection rule.

Our hypotheses are

$\begin{array}{l} H_{0} : p = 0.01 & versus & H_{a} : p > 0.01 \end{array}$

where $p$ represents the population proportion of American Internet users who are married or in a long-term relationship and who met on a blind date or through a dating service. We will reject $H_{0}$ if the $p$ -value # 0.05.
Step 2 Calculate $Z_{data}$ .

We use the instructions supplied in the Step-by-Step Technology Guide on page 552. Figure 37 shows the TI-83/84 results from the $Z$ test for $p$ , Figure 38 shows the results from Minitab, and Figure 39 shows the results from CrunchIt!.

FIGURE 37 TI-83/84 results.

Page 549

Note: Minitab, TI-83/84, and CrunchIt! round results to different numbers of decimal places.

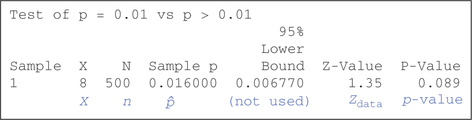FIGURE 38 Minitab results.

We have

$Z_{data} = \frac{\hat{p} - p_{0}}{\sqrt{\frac{p_{0} \cdot q_{0}}{n}}} = \frac{0.016 - 0.01}{\sqrt{\frac{(0.01) (0.99)}{500}}} \approx 1.348399725$

which concurs with the TI-83/84 results in Figure 37.
Step 3 Find the $p$ -value.

From Figures 37, 38, 39, and 40 we have

$p -value = P (Z > 1.348399725) = 0.0887649866 \approx 0.08876$

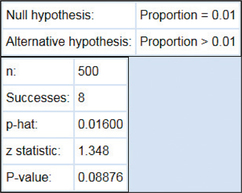FIGURE 39 CrunchIt! results.

FIGURE 40 $p$ -Value for a right-tailed test.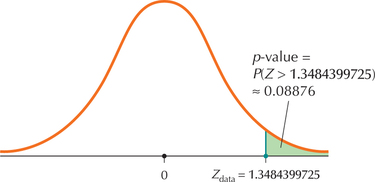
Step 4 State the conclusion and interpretation.

Because $p-value \approx 0.08876$ is $n o t \leq α = 0.05$ , we do not reject $H_{0}$ . There is insufficient evidence that the population proportion of American Internet users who are married or in a long-term relationship and who met on a blind date or through a dating service has increased.