EXAMPLE 31 test for using the critical-value method

carbonemissions8

State Carbon emissions
(millions of metric tons)
Florida 230.98
Kentucky 148.36
Missouri 135.54
New Hampshire 16.41
New Mexico 56.60
New York 166.32
Tennessee 105.73
Virginia 99.86
Table 9.42: Carbon emissions

The table contains the carbon emissions from all sources for a random sample of eight states. Test whether the population standard deviation of carbon emissions differs from 60 million metric tons, using level of significance .

558

Solution

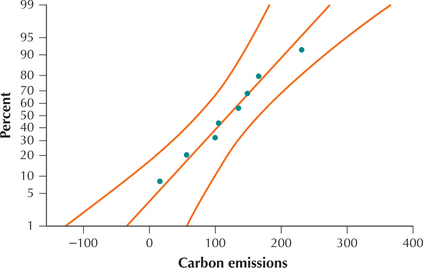
The normal probability plot indicates acceptable normality.

image

  • Step 1 State the hypotheses.

    The phrase “differs from” indicates that we have a two-tailed test. The value answers the question “Differs from what?” (Note that is 60, and not 60,000,000 because the data are expressed in millions.) Thus, we have our hypotheses:

    where represents the population standard deviation of carbon emissions in millions of metric tons.

  • Step 2 Find the critical values and state the rejection rule.

    We have , so . Because is given as 0.05, and . Then, from the table (Appendix Table E), we have , and . We will reject if is either or .

  • Step 3 Find .

    The descriptive statistics in Figure 43 tell us that the sample variance is , squared.

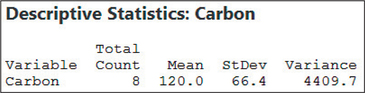    image
    Figure 9.54: FIGURE 43 Descriptive statistics from Minitab.

    Thus, our test statistic is:

  • Step 4 State the conclusion and the interpretation.

    In Step 2, we said that we would reject if was either . Because is neither (see Figure 44), we do not reject . There is insufficient evidence at level of significance that the population standard deviation of the state carbon emissions differs from 60 million.

    559

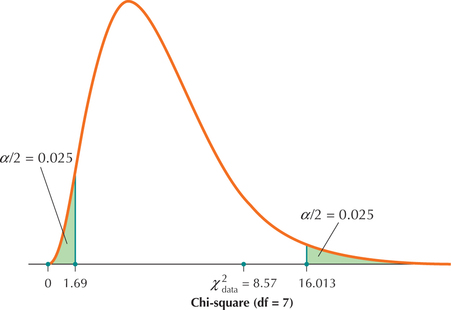    image
    Figure 9.55: FIGURE 44 does not fall in critical region, so do not reject .

NOW YOU CAN DO

Exercises 7–12.