Example 32

EXAMPLE 32 $χ^{2}$ test for $σ$ using the $p$ -value method and technology

The table contains the calories in ten entrée food items, courtesy of Food-A-Pedia. Test whether the population standard deviation is larger than 100 calories, using level of significance $α = 0.05$ .

entreecalories

Entrée item	Calories	Entrée item	Calories
Grilled steak	387	Ground beef (95% lean, medium patty)	167
Fried steak	440	Grilled pork chop (large)	314
Breaded fried steak	600	Fried pork chop (large)	326
Ground beef (75% lean, medium patty)	234	Meat pizza, thin crust, large	325
1 large BBQ short rib with sauce	148	Fried catfish (breaded or battered)	276

Solution

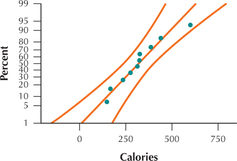
The normal probability plot in Figure 45 indicates acceptable normality, allowing us to proceed with the hypothesis test.

FIGURE 45 Normal probability plot of calories.

Step 1 State the hypotheses and the rejection rule.

The phrase “larger than” indicates that we have a right-tailed test. The question “Larger than what?” tells us that $σ_{0} = 100$ , giving us

$\begin{array}{l} H_{0} : σ = 100 & versus & H_{a} : σ > 100 \end{array}$

We reject $H_{0}$ if the $p-value \leq α = 0.05$ .
Step 2 Find $χ_{data}^{2}$ .

We use the Step-by-Step Technology Guide on page 562. The Minitab descriptive statistics in Figure 46 tell us that the sample variance is $s^{2} = 17, 742.5$ calories squared.

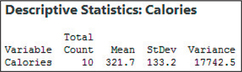FIGURE 46 Calories descriptive statistics.

Thus,

$χ_{data}^{2} = \frac{(n - 1) s^{2}}{σ_{0}^{2}} = \frac{(10 - 1) (17, 742.5)}{100^{2}} \approx 15.97$
Step 3 Find the $p$ -value.

For our right-tailed test, Table 14 tells us that

$p -value = P (χ^{2} > χ_{data}^{2}) = P (χ^{2} > 15.97)$

That is, the $p$ -value is the area to the right of $χ_{data}^{2} = 15.97$ , as shown in Figure 47. To find the $p$ -value, we use the instructions provided in the Step-by-Step Technology Guide provided at the end of this section. The TI-83/84 results shown in Figure 48 tell us that $p-value = P (χ^{2} > 15.97) = 0.0675107153 \approx 0.0675$ .

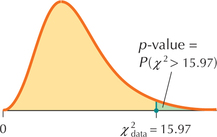FIGURE 47 $p$ -Value for $χ^{2}$ test

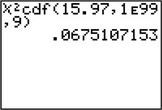FIGURE 48 TI-83/84 results.
Step 4 State the conclusion and the interpretation.

Because $p-value = 0.0675$ is not $\leq α = 0.05$ , we do not reject $H_{0}$ . There is insufficient evidence that the population standard deviation is greater than 100 calories.

NOW YOU CAN DO

Exercises 13–18.