Example 34

EXAMPLE 34 Calculating $β$ , the probability of a Type II error

ATM network operator Star Systems of San Diego reported that active users of debit cards used them an average of 11 times per month. Suppose we are interested in testing whether people use debit cards on average more than 11 times per month, using level of significance $α = 0.01$ . The hypotheses are

$\begin{array}{l} H_{0} : μ = 11 & versus & H_{a} : μ > 11 \end{array}$

Page 566

where $μ$ represents the population mean debit card usage per month. Suppose we have $n = 36, \bar{x} = 11.5$ , and $σ = 3$ , and from Table 4 (page 500) we have $Z_{crit} = 2.33$ .

State what a Type II error would be in this case.
Let $μ_{a} = 13$ . That is, suppose the population mean debit card usage is actually 13 times per month. Calculate $β$ , the probability of making a Type II error when $μ_{a} = 13$ .

Solution

We make a Type II error when we do not reject $H_{0}$ when $H_{0}$ is false. In this case, a Type II error would be to conclude that the population mean debit card usage was 11 times per month when in actuality it was more than 11 times per month.
We follow the steps for calculating $β$ .
- Step 1 We have a right-tailed test, so that
  
  ${\bar{x}}_{crit} = μ_{0} + z_{crit} \cdot \frac{σ}{\sqrt{n}} = 11 + 2.33 \cdot \frac{3}{\sqrt{36}} = 12.165$
- Step 2 Figure 49 shows the normal curve centered at $μ_{a} = 13$ , with ${\bar{x}}_{crit} = 12.165$ labeled.
  
  FIGURE 49 $β$ probability of Type II error.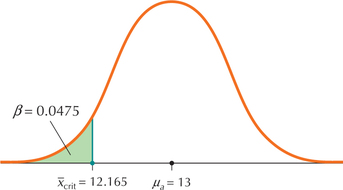
- Step 3 The right-tailed test tells us that $β$ equals the area under the normal curve drawn in Step 2 to the left of ${\bar{x}}_{crit} = 12.165$ . This is the shaded area in Figure 49. Area represents probability, so we have
  
  $β = p (\bar{x} < 12.165) when μ_{a} = 13$
  
  Standardizing with $μ_{a} = 13, σ = 3$ , and $n = 36$ :
  
  $\begin{matrix} β = P (\bar{x} < 12.165) \\ = P (Z < \frac{12.165 - 13}{3 / \sqrt{36}}) \\ = P (Z < - 1.67) = 0.0475 \end{matrix}$
  
  This is a Case 1 problem from Table 8 of Chapter 6 on page 355.
  
  Thus, $β = 0.0475$ . This represents the probability of making a Type II error, that is, of not rejecting the hypothesis that the population mean debit card usage is 11 times per month when in actuality it is 13 times per month.

NOW YOU CAN DO

Exercises 5–16.