EXAMPLE 9 Test for , critical-value method, right-tailed test

image Clothing Store Sales

For the situation in Example 7, test at level of significance whether the population mean total sales per customer is more than $413.

Solution

We may apply the test because the sample is large , and the population standard deviation σ is known.

503

  • Step 1 State the hypotheses.

    From Example 7, our hypotheses are

    where represents the population mean total sales per customer.

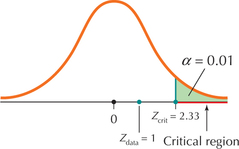    image
    Figure 9.3: FIGURE 3 Critical region for a right-tailed test.

  • Step 2 Find and state the rejection rule.

    We have a right-tailed test and level of significance , which, from Table 4, tell us that . Because we have a right-tailed test, the rejection rule will be “Reject if ,” that is, “Reject if ” (see Figure 3).

  • Step 3 Find .

    From Example 7, we have .

  • Step 4 State the conclusion and interpretation.

    Our rejection rule states that we will reject if . Because , which is not ≥ 2.33, the conclusion is to not reject (Figure 4). Even though the sample mean of exceeds , it does not do so by a wide enough margin to overcome the reasonable doubt that the difference between and may have been due to chance. We interpret our conclusion as follows: “There is insufficient evidence at the 0.01 level of significance that the population mean total sales is greater than $413 per customer over the six-month period.”

NOW YOU CAN DO

Exercises 37–40.