Section 3.1 Exercises

CLARIFYING THE CONCEPTS

Question 3.1

1. Explain what a measure of center is. (p. 108)

3.1.1

A value that locates the center of the data set.

Question 3.2

2. Which measure may be used as the balance point of the data set? Explain how this works. (p. 110)

Question 3.3

3. Explain what we mean when we say that the mean is sensitive to the presence of extreme values. Explain whether the median is sensitive to extreme values. (pp. 111-112)

3.1.3

Because the mean depends in part on the sum of all data values, an outlier will skew the mean (pull it in one direction or another). Since the median simply depends on position in an ordered list, it is not sensitive to outliers.

Question 3.4

4. What are the three measures of center that we learned about in this section? (p. 108)

For Exercises 5–12, either state what is being described or provide the notation.

Question 3.5

5. The number of observations in your sample data set (p. 109)

3.1.5

Sample size (n)

Question 3.6

6. The number of observations in your population data set (p. 109)

Question 3.7

7. Notation denoting “sum all the data” (p. 109)

3.1.7

Question 3.8

8. Notation for what we get when we add up all the data values in the population, and divide by how many observations there are in the population (p. 109)

Question 3.9

9. Notation for what we get when we add up all the data values in the sample, and divide by how many observations there are in the sample (p. 109)

3.1.9

Question 3.10

10. The middle data value when the data are put in ascending order (p. 112)

Question 3.11

11. The data value that occurs with the greatest frequency (p. 114)

3.1.11

Mode

Question 3.12

12. The sample mean (p. 109)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 13–18 Example 1 Population mean
Exercises 19–24 Example 2 Sample mean
Exercises 25–30 Example 3 Sensitivity of mean
Exercises 31–36 Example 4 Median
Exercises 37–40 Example 6 Mode
Exercises 41–44 Example 7 Mean, median, and
skewness

For the data in Exercises 13–18:

  1. Find the population size .
  2. Calculate the population mean .

Question 3.13

13. State exports to other countries are shown in the table for the population of all New England states, for the month of June 2014, expressed in billions of dollars.

119

State Exports State Exports
Connecticut 1.4 New Hampshire 0.4
Maine 0.3 Rhode Island 0.2
Massachusetts 2.4 Vermont 0.3
Table 3.7: Source: U.S. Census Bureau.

3.1.13

(a) 6 (b) $0.83 billion

Question 3.14

14. The number of wins for each baseball team in the population of the American League West division for 2013 is shown in the table.

Team Wins Team Wins
Oakland Athletics 96 Seattle Mariners 71
Texas Rangers 91 Houston Astros 51
Los Angeles Angels 78
Table 3.8: Source: www.mlb.com.

Question 3.15

15. The table provides the motor vehicle theft rate for the population of the top 10 countries in the world for motor vehicle theft, for 2012. The theft rate equals the number of motor vehicles stolen in 2012 per 100,000 residents.

Country Theft rate Country Theft rate
Italy 208.0 Greece 100.2
France 174.1 Norway 94.1
USA 167.8 Netherlands 75.2
Sweden 117.2 Spain 75.1
Belgium 106.0 Cyprus 66.0
Table 3.9: Source: United Nations Office on Drugs and Crime.

3.1.15

(a) 10 (b) 118.37 motor vehicles stolen per 100,000 residents

Question 3.16

16. The National Center for Education Statistics sponsors the Trends in International Mathematics and Science Study (TIMSS). The table contains the mean science scores for the eighth-grade science test for the populations of all Asian-Pacific countries that took the exam.

Country Science score Country Science score
Singapore 578 Australia 527
Taiwan 571 New Zealand 520
South Korea 558 Malaysia 510
Hong Kong 556 Indonesia 420
Japan 552 Philippines 377

Question 3.17

17. The table contains the number of petit larceny cases for the population of all police precincts in South Manhattan in 2013.

Precinct Petit larcenies Precinct Petit larcenies
1 2014 10 995
5 1288 13 2094
6 1555 14 4551
7 584 17 823
9 1607 18 2071
Table 3.11: Source: New York City Police Department.

3.1.17

(a) 10 (b) 1758.2 petit larceny cases

Question 3.18

18. The table contains the number of criminal trespass cases for the population of all police precincts in South Manhattan in 2013.

Precinct Criminal
trespasses		 Precinct Criminal
trespasses
1 108 10 207
5 105 13 135
6 113 14 340
7 233 17 74
9 219 18 120
Table 3.12: Source: New York City Police Department.

For the data in Exercises 19–24:

  1. Find the sample size .
  2. Calculate the sample mean .

Question 3.19

19. A sample of the state export data from Exercise 13 is provided in the table.

State Exports
Connecticut 1.4
Massachusetts 2.4
Rhode Island 0.2

3.1.19

(a) 3 (b) $1.33 billion

Question 3.20

20. A sample from the baseball data in Exercise 14 is shown here.

Team Wins
Texas Rangers 91
Los Angeles Angels 78
Seattle Mariners 71

Question 3.21

21. A sample from the motor vehicle theft data in Exercise 15 is as follows.

Country Theft rate
Italy 208.0
USA 167.8
Greece 100.2

3.1.21

(a) 3 (b) 158.67 motor vehicles stolen per 100,000 residents

Question 3.22

22. A sample from the science score data in Exercise 16 is given here.

Country Science score
South Korea 558
Hong Kong 556
Japan 552
Australia 527

Question 3.23

23. The following sample is taken from the petit larceny data in Exercise 17.

Precinct Petit larcenies
1 2014
6 1555
9 1607
14 4551
17 823

3.1.23

(a) 5 (b) 2110 petit larceny cases

120

Question 3.24

24. A sample taken from the criminal trespass data in Exercise 18 is as follows.

Precinct Criminal
trespasses
1 108
7 233
14 340
18 120

For Exercises 25–30, use the data from the indicated exercise, along with the indicated extreme, to show that the mean is more sensitive to extreme values. For each exercise, find the sample mean including the extreme value. Compare your answer to the mean calculated without the extreme value from the earlier exercise.

Question 3.25

25. Data from Exercise 19.

3.1.25

$3.5 billion, larger than $1.33 billion

Question 3.26

26. Data from Exercise 20.

Question 3.27

27. Data from Exercise 21.

3.1.27

369, larger than 158.67

Question 3.28

28. Data from Exercise 22.

Question 3.29

29. Data from Exercise 23.

3.1.29

5091.67 petit larceny cases, larger than 2110 petit larceny cases

Question 3.30

30. Data from Exercise 24.

For Exercises 31–36, use the data from the indicated exercise, along with the indicated extreme, to show that the mean is more sensitive to extreme values than the median is. Do the following:

  1. Calculate the median of the data without the extreme value.
  2. Find the median of the data including the extreme value. Compare your answers from (a) and (b). Note that the median did not change as much as the mean did in Exercises 25–30.

Question 3.31

31. Data from Exercise 19.

3.1.31

(a) $1.4 billion (b) $1.9 billion

Question 3.32

32. Data from Exercise 20.

Question 3.33

33. Data from Exercise 21.

3.1.33

(a) 167.8 motor vehicles stolen per 100,000 residents (b) 187.9 motor vehicles stolen per 100,000 residents

Question 3.34

34. Data from Exercise 22.

Question 3.35

35. Data from Exercise 23.

3.1.35

(a) 1607 petit larceny cases (b) 1810.5 petit larceny cases

Question 3.36

36. Data from Exercise 24.

For the data in Exercises 37–40, find the mode.

Question 3.37

37. The table contains the number of dangerous weapons cases for four police precincts in Manhattan.

Precinct Dangerous weapons cases
1 19
5 24
20 24
22 9

3.1.37

24 dangerous weapons cases

Question 3.38

38. The Recording Industry Association of America (RIAA) awards multi-platinum status for any musical recording that sells more than 2 million copies. The table contains a random sample of 10 of the musical artists with the most multi-platinum singles.

Artist Multi-
platinums		 Artist Multi-
platinums
Beyoncé 4 Linkin Park 2
Bruno Mars 4 The Beatles 4
Jay-Z 4 Michael Jackson 1
Katy Perry 8 Taylor Swift 8
Lady Gaga 6 Tim McGraw 2
Table 3.20: Source: RIAA.

Question 3.39

39. The table contains the unemployment rates in August 2014 for 10 countries.

Country Unemployment
rate		 Country Unemployment
rate
Britain 6.4 Japan 3.7
Canada 7.0 Mexico 4.8
China 4.1 Pakistan 6.2
India 8.8 South Korea 3.4
Italy 12.3 United States 6.2
Table 3.21: Source: The Economist, www.economist.com/node/21604509.

3.1.39

6.2

Question 3.40

40. The table contains the top 10 most downloaded free apps for the IOS platform, as reported by Apple.com, along with the app type, for June 2014. Find the mode of App Type.

Rank App App
type		 Rank App App
type
1 Two Dots Games 6 Snap Chat Photo
and video
2 The Line Games 7 Instagram Photo
and video
3 Traffic Racer Games 8 The Test Games
4 Rival
Knights		 Games 9 Republique Games
5 Piano Tiles Games 10 YouTube Photo
and video

For Exercises 41–44, consider the accompanying distributions. What can we say about the values of the mean, median, and mode in relation to one another for the given histograms?

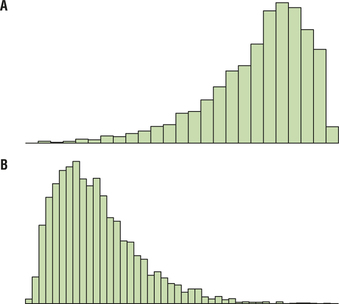
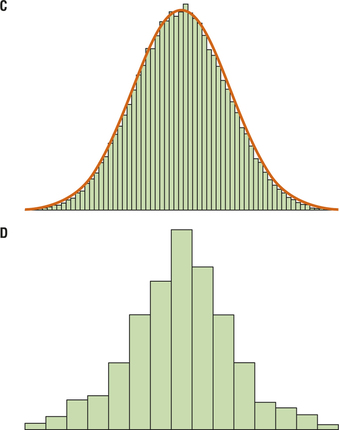
image
image

121

Question 3.41

41. The distribution in A

3.1.41

Mean < Median < Mode

Question 3.42

42. The distribution in B

Question 3.43

43. The distribution in C

3.1.43

Mean = Median = Mode

Question 3.44

44. The distribution in D

APPLYING THE CONCEPTS

Question 3.45

45. NFL Football, Southern Style. The table contains the population of all the teams in the National Football Conference South Division, along with the number of wins in the 2013 season.

  1. What is the population size, , where the population is the NFC South Division?
  2. What is the population mean number of wins, ?
NFC South team Wins
Carolina Panthers 12
New Orleans Saints 11
Atlanta Falcons 4
Tampa Bay Buccaneers 4

3.1.45

(a) 4 (b) 7.75 wins

Question 3.46

46. New England Electoral Votes. The table contains the population of all the New England states, along with their electoral votes.

  1. What is the population size, ?
  2. Calculate the population mean number of electoral votes, .
Electoral votes
Connecticut 7
Maine 4
Massachusetts 11
New Hampshire 4
Rhode Island 4
Vermont 3

Question 3.47

47. NFL Football, Southern Style. Refer to the population data in Exercise 45. Suppose we take a sample from the population, and we get the Carolina Panthers and the Atlanta Falcons.

  1. What is the sample size ?
  2. Calculate the sample mean number of wins, .

3.1.47

(a) 2 (b) 8 wins

Question 3.48

48. New England Electoral Votes. Refer to the population data in Exercise 46. Suppose we take a sample from the population, and get Massachusetts, Rhode Island, and Vermont.

  1. What is the sample size ?
  2. Calculate the sample mean number of electoral votes, .

Video Game Sales. The Chapter 1 Case Study looked at video game sales for the top 30 video games. The following table contains the total sales (in game units) and weeks on the top 30 list for a sample of five randomly selected video games. Use this information for Exercises 49 and 50.

Video game Total sales in
millions of
units		 Weeks
Super Mario Bros. U for WiiU 1.7 78
NBA 2K14 for PS4 0.6 27
Battlefield 4 for PS3 0.9 29
Titanfall for XBoxOne 1.2 10
Yoshi's New Island for 3DS 0.2 10
Table 3.25: Source: www.vgchartz.com.

Question 3.49

videogamereg

49. Find the following measures of center for total sales.

  1. Mean
  2. Median

3.1.49

(a) 0.92 million units (b) 0.9 million units

Question 3.50

videogamereg

50. Calculate the following measures of center for weeks.

  1. Mean
  2. Median

image Darts and the Dow Jones.

The following table contains a random sample of eight days from the Chapter 3 Case Study data set, indicating the stock market gain or loss for the portfolio chosen by the random darts, as well as the Dow Jones Industrial Average gain or loss for that day. Use this information for Exercises 51 and 52.

Question 3.51

51. Find the following measures of center for the darts stock returns.

  1. Mean
  2. Median

3.1.51

(a) 9.45 (b) 14.05

Question 3.52

dartsdjia

52. Find the following measures of center for the DJIA.

  1. Mean
  2. Median

122

Darts DJIA
−27.4 −12.8
18.7 9.3
42.2 8
−16.3 −8.5
11.2 15.8
28.5 10.6
1.8 11.5
16.9 −5.3
Table 3.26: Source: Wall Street Journal.

Age And Height. The following table provides a random sample from the Chapter 4 Case Study data set body_females, showing the age and height of the eight women. Use this information for Exercises 53 and 54.

Age Height
40 63.5
28 63
25 64.4
34 63
26 63.8
21 68
19 61.8
24 69
Table 3.27: Source: Journal of Statistics Education.

Question 3.53

ageheight

53. Find the following measures of center for the women's ages.

  1. Mean
  2. Median

3.1.53

(a) 27.125 years (b) 25.5 years

Question 3.54

ageheight

54. Find the following measures of center for the women's heights.

  1. Mean
  2. Median

Saturated Fat and Calories. The table contains the calories and saturated fat in a sample of ten food items. Use this information for Exercises 55 and 56.

Question 3.55

satfatcorr

55. Find the following measures of center for calories.

  1. Mean
  2. Median

3.1.55

(a) 192.2 calories (b) 172 calories

Question 3.56

satfatcorr

56. Find the following measures of center for the grams of saturated fat.

  1. Mean
  2. Median

Food item Calories Grams of
saturated fat
Chocolate bar (1.45 ounces) 216 7.0
Meat & veggie pizza
(large slice)		 364 5.6
New England clam chowder
(1 cup)		 149 1.9
Baked chicken drumstick
(no skin, medium size)		 75 0.6
Curly fries, deep-fried
(4 ounces)		 276 3.2
Wheat bagel (large) 375 0.3
Chicken curry (1 cup) 146 1.6
Cake doughnut hole (one) 59 0.5
Rye bread (1 slice) 67 0.2
Raisin bran cereal (1 cup) 195 0.3
Table 3.28: Source: Food-a-Pedia.

Table 6 contains the trade balance currently maintained by the United States with a sample of 9 countries, for the month of June 2014. Use this data for Exercises 57–60.

Table 3.29: Table 6 Trade balance
Country Trade balance
($ billions)
Brazi 1
France −1.2
Germany −5.6
India −1.3
Italy −2.4
Japan −5.6
South Korea −1.8
Saudi Arabia −1.8
United Kingdom 0
Table 3.29: Source: Foreign Trade Division, U.S. Census Bureau.

Question 3.57

57. Find the sample size, .

3.1.57

9

Question 3.58

58. Calculate the sample mean trade balance, .

Question 3.59

59. Find the median.

3.1.59

–$1.8 billion

Question 3.60

60. Find the modes.

Table 7 contains the number of cylinders, the engine size (in liters), the fuel economy (miles per gallon [mpg], city driving), and the country of manufacture for six 2011 automobiles. Use this information for Exercises 61–65.

123

Table 3.30: Table 7 Cylinders, engine size, and fuel economy for six cars
Vehicle Cylinders Engine
size		 City
mpg		 Country of
manufacture
Cadillac CTS 6 3.0 18 USA
Ford Fusion Hybrid 4 2.5 41 USA
Ford Taurus 6 3.5 18 USA
Honda Civic 4 1.8 25 Japan
Rolls Royce 12 6.7 11 UK
Toyota Camry
Hybrid		 4 2.4 31 Japan
Table 3.30: Source: www.fueleconomy.gov.

Question 3.61

cylinderengine

61. Find the following for the number of cylinders:

  1. Mean
  2. Median
  3. Mode

3.1.61

(a) 6 cylinders (b) 5 cylinders (c) 4 cylinders

Question 3.62

cylinderengine

62. Refer to your work in Exercise 61. Which measure of center do you think is most representative of the typical number of cylinders? Explain.

Question 3.63

cylinderengine

63. Find the following for the engine size:

  1. Mean
  2. Median
  3. Mode

3.1.63

(a) 3.317 liters (b) 2.75 liters (c) No mode

Question 3.64

cylinderengine

64. Find the following for the city mpg:

  1. Mean
  2. Median
  3. Mode

Question 3.65

cylinderengine

65. Find the mode for country of manufacture.

3.1.65

USA

Use the information in Table 8 to answer Exercises 66–68, which gives the number of wins for the top 10 NASCAR racing drivers in various categories.

Table 3.31: Table 8 Top 10 NA SCAR winners in the modern era
Rank Driver Total Super
speedways		 Short
tracks
1 Darrell Waltrip 84 18 47
2 Dale Earnhardt 76 29 27
3 Jeff Gordon 75 15 15
4 Cale Yarborough 69 15 29
5 Richard Petty 60 19 23
6 Bobby Allison 55 24 12
7 Rusty Wallace 55 5 25
8 David Pearson 45 20 1
9 Bill Elliott 44 16 2
10 Mark Martin 35 5 7
Table 3.31: Source: www.nascar.com.

Question 3.66

nascar

66. Refer to the super speedways data. Find the following:

  1. Mean
  2. Median
  3. Mode

Question 3.67

nascar

67. Refer to the short tracks data. Find the following:

  1. Mean
  2. Median
  3. Mode

3.1.67

(a) Mean = 18.8 (b) Median = 19 (c) No mode

Question 3.68

nascar

68. Refer to the totals data. Find the following:

  1. Mean
  2. Median
  3. Mode

For Exercises 69–73, refer to Table 9, which lists the top five mass market paperback fiction books for the week of July 1, 2014, as reported by the New York Times.

Table 3.32: Table 9 Top five best-sellers in paperback trade fiction
Rank Title Author Price
1 A Game of Thrones George R. R. Martin $7.83
2 Takedown Twenty Janet Evanovich $7.64
3 Inferno Dan Brown $8.48
4 A Dance with Dragons George R. R. Martin $6.71
5 The 9th Girl Tami Hoag $8.47

Question 3.69

69. Find the mean, median, and mode for the price of these five books on the best-seller list. Suppose a salesperson claimed that the price of a typical book on the best-seller list is less than $14. How would you use these statistics to respond to this claim?

3.1.69

$7.83, 7.83, no mode, A typical book on the best-sellers list would cost less than $14.00 since the mean and median are all less than $14.

Question 3.70

70. Linear transformations. Add $10 to the price of each book.

  1. Now find the mean of these new prices.
  2. How does this new mean relate to the original mean?
  3. Construct a rule to describe this situation in general.

Question 3.71

71. Linear transformations. Multiply the price of each book by 5.

  1. Now find the mean of these new prices.
  2. How does this new mean relate to the original mean?
  3. Construct a rule to describe this situation in general.

3.1.71

(a) $39.13 (b) The new mean is 5 times the original mean. (c) If each value of a data set is multiplied by a number , the mean of the resulting data set will be the mean of the original data set times .

Question 3.72

72. Find the mode for the following variables:

  1. Price
  2. Author

Question 3.73

73. Explain whether it makes sense to find the mean or median of the variable author.

3.1.73

It does not make sense to find the mean and the median of the variable author because the variable author is a categorical variable.

Mode of Categorical Data. The New York City Police Department tracks the number and type of traffic violations. The table contains a random sample of 12 traffic violations and the borough in which they occurred (Manhattan or Brooklyn). Use the data for Exercises 74–76.

Violation type Borough Violation type Borough
Cell phone Brooklyn Disobey sign Manhattan
Safety belt Manhattan Speeding Brooklyn
Cell phone Brooklyn Safety belt Manhattan
Cell phone Manhattan Disobey sign Manhattan
Speeding Brooklyn Disobey sign Brooklyn
Safety belt Manhattan Cell phone Manhattan

Question 3.74

74. Find the mode for violation type. Does this mean that most violations are of this type?

Question 3.75

75. Calculate the mode for borough.

3.1.75

Manhattan

Question 3.76

76. Does the idea of the mean or median of these two variables make any sense? Explain clearly why not.

124

Car Model Years. The dotplot in Figure 9 represents the model year for a sample of cars in a used car lot. Refer to the dotplot for Exercises 77–79.

image
Figure 3.9: FIGURE 9 Dotplot of model year.

Question 3.77

77. What are the mean, median, and mode of the model year?

3.1.77

Mean = 2013.5, Median = 2014, Mode = 2015

Question 3.78

78. Calculate a new statistic “age of the car in 2015” as follows: take the model year and subtract it from 2015.

  1. Find the mode of the car ages.
  2. Find the mean and median of the car ages.

Question 3.79

79. What will be the mean, median, and mode of the car ages in 2025?

3.1.79

Mean = 11.5 years, Median = 11 years, Mode = 10 years

Question 3.80

80. Five friends have just had dinner at the local pizza joint. The total bill came to $30.60. What is the mean cost of each person's meal?

Question 3.81

81. Lindsay just bought four shirts at the boutique in the mall, costing a total of $84.28. What was the mean cost of each shirt?

3.1.81

$21.07

Dealing with Missing Data. Exercises 82–85 ask you to calculate measures of center when one of the values is missing.

Question 3.82

82. The mean cost of a sample of five items is $20. The cost of four of the items is as follows: $25, $15, $15, $20. What is the cost of the 5th item?

Question 3.83

83. The mean size of four downloaded music files is 3 Mb (megabytes). The size of three of the files is as follows: 5 Mb, 2 Mb, 3 Mb. What is the length of the 4th music file?

3.1.83

2 Mb

Question 3.84

84. The median number of students in a sample of seven statistics classes is 25. The ordered values are: 20, 22, 24, __, 27, 27, 28. What is the missing value?

Question 3.85

85. The median number of academic credits taken in a sample of six students is 15. The ordered values are: 12, 12, 14, __, 17, 17. What is the missing value?

3.1.85

16

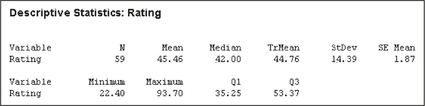
Nutrition Ratings of Breakfast Cereals. Refer to the following information for Exercises 86–89. (Note that Minitab denotes both the sample size and the population size as .) The data represent the nutrition rate of 59 cereals based on sugar content, vitamin content, and so on.

image

Question 3.86

86. Find the following sample statistics.

  1. The sample size
  2. The sample mean
  3. The sample median
  4. The highest and lowest ratings in the sample

Question 3.87

87. What do these statistics tell us about the skewness of the distribution?

3.1.87

The mean is larger than the median, which implies the distribution is positively skewed.

Question 3.88

88. Linear Transformations. If we take each cereal rating and subtract 5 from it, how would that affect the mean, median, and mode? Would it affect each of the measures equally?

Question 3.89

89. Linear Transformations. If we cut each of the cereals' ratings in half, how would that affect the mean, median, and mode? Would it affect each of the measures equally?

3.1.89

The mean, median and mode will all be halved. Each statistic will be affected equally.

BRINGING IT ALL TOGETHER

Pulse Rates for Men and Women. To answer Exercises 90–93, refer to Figure 10, which includes comparative dotplots of the pulse rates for males and females.2

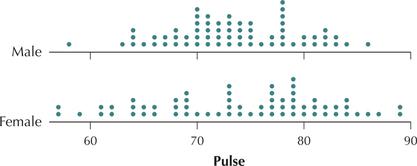
image
Figure 3.10: FIGURE 10 Comparative dotplots of pulse rates, by gender.

Question 3.90

90. Examine Figure 10.

  1. Without doing any calculations, what is your impression of which gender, if any, has the higher overall pulse rate?
  2. Find the mean pulse rate for the males by estimating the location of the balance point.
  3. Find the mean pulse rate for the females by estimating the location of the balance point.
  4. Based on (b) and (c), which gender has the higher mean pulse rate? Does this agree with your earlier impression?

Question 3.91

91. Find the following medians:

  1. The median pulse rate for the males
  2. The median pulse rate for the females
  3. Which gender has the higher median pulse rate? Does this agree with your findings for the mean earlier?

3.1.91

(a) 73 (b) 76 (c) Females; yes

Question 3.92

92. Find the following modes:

  1. The mode pulse rate for the males
  2. The mode pulse rate for the females
  3. Which gender has the higher mode pulse rate? Does this agree with your findings for the mean earlier?

Question 3.93

image 93. What if the fastest pulse rate for the men was a typo and should have been an unspecified lower pulse rate? Describe how and why this change would have affected the following, if at all. Would they increase, decrease, or remain unchanged? Or is there insufficient information to tell what would happen? Explain your answers.

  1. The mean men's pulse rate
  2. The median men's pulse rate
  3. The mode men's pulse rate

125

3.1.93

(a) Decrease (b) Unchanged (c) Unchanged

Question 3.94

statebusinesses

94. Trimmed Mean. Because the mean is sensitive to extreme values, the trimmed mean was developed as another measure of center. To find the 10% trimmed mean for a data set, omit the largest 10% of the data values and the smallest 10% of the data values, and calculate the mean of the remaining values. Because the most extreme values are omitted, the trimmed mean is less sensitive, or more robust (resistant), than the mean as a measure of center. For the data in the table, calculate the following:

  1. The mean
  2. The 10% trimmed mean
  3. The 20% trimmed mean

The data represent the number of business establishments in a sample of states.

State Businesses
(1000s)		 State Businesses
(1000s)
Alabama 3.8 Michigan 7.5
Arizona 7.9 Minnesota 6.1
Colorado 8.9 Missouri 5.9
Connecticut 3.1 Ohio 9.5
Georgia 10.3 Oklahoma 3.8
Illinois 11.9 Oregon 5.4
Indiana 5.6 South Carolina 4.6
Iowa 2.7 Tennessee 5.4
Maryland 5.7 Virginia 8.6
Massachusetts 6.3 Washington 9.3
Table 3.34: Source: U.S. Census Bureau.

Question 3.95

95. Challenge Exercise. In general, would you expect the trimmed mean to be larger, smaller, or about the same as the mean for data sets with the following shapes?

  1. Right-skewed data
  2. Left-skewed data
  3. Symmetric data

3.1.95

(a) Smaller (b) Larger (c) Same

Question 3.96

96. Midrange. Another measure of center is the midrange.

Because the midrange is based on the maximum and minimum values in the data set, it is not a robust statistic, but it is sensitive to extreme values. Calculate the midrange for the following data:

  1. The price data from Table 9 on page 123.
  2. The car model year data from Figure 9 on page 124.

Question 3.97

97. Harmonic Mean. The harmonic mean is a measure of center most appropriately used when dealing with rates, such as miles per hour (mph). The harmonic mean is calculated as

where is the sample size and the 's represent rates, such as the speeds in mph. Emily walked five miles today, but her walking speed slowed as she walked farther. Her walking speed was 5 mph for the first mile, 4 mph for the second mile, 3 mph for the third mile, 2 mph for the fourth mile, and 1 mph for the fifth mile. Calculate her harmonic mean walking speed over the entire five miles.

3.1.97

2.190 mph

Question 3.98

98. Challenge Exercise. The (arithmetic) mean for Emily's five-mile walk in Exercise 97 is 3 mph. Explain clearly why the value you calculated for the harmonic mean in Exercise 97 makes more sense than this arithmetic mean of 3 mph. (Hint: Consider time.)

Question 3.99

99. Geometric Mean. The geometric mean is a measure of center used to calculate growth rates. Suppose that we have positive values; then the geometric mean is the th root of the product of the values. Jamal has been saving money in an account that has had 4% growth, 6% growth, and 10% growth over the last three years. Calculate the average growth rate over these three years. (Hint: Find the geometric mean of 1.04, 1.06, and 1.10 and subtract 1.)

3.1.99

Geometric mean = 1.0664, 6.64% growth

CONSTRUCT YOUR OWN DATA SETS

Question 3.100

100. Construct your own data set with , where the mean, the median, and the mode are all the same. Yes, just make up your own list of numbers, as long as the mean, median, and mode are all the same. Draw a dotplot. Comment on the skewness of the distribution.

Question 3.101

101. Construct your own data set with , where the mean is greater than the median, which is greater than the mode. Draw a dotplot. Comment on the skewness of the distribution.

3.1.101

Answers will vary.

Question 3.102

102. Construct your own data set with , where the mode is greater than the median, which is greater than the mean. Draw a dotplot. Comment on the skewness of the distribution.

Question 3.103

103. Construct your own data set with . Let the mean and median be equal. Now, alter the three data values so that the mean of the altered data set has increased, while the median of the altered data set has decreased.

3.1.103

Answers will vary.

Use the Mean and Median applet for Exercises 104 and 105.

Question 3.104

104. Insert three points on the line by clicking just below it: two near the left side and one near the middle.

  1. Click and drag the rightmost point to the right.
  2. Describe what happens to the mean when you do this.
  3. Describe what happens to the median when you do this.

Question 3.105

105. Explain why each of the measures behaves the way it does in the previous exercise.

3.1.105

Answers will vary.

WORKING WITH LARGE DATA SETS

Open the VideoGameSales data set from the Chapter 1 Case Study. The data set represents a sample. Use technology to do the following. image videogamesales

Question 3.106

videogamesales

106. Find the mean and median weekly sales.

Question 3.107

videogamesales

107. Suppose we remove the biggest seller for the week, Minecraft for PS3, from the data. Given what you have learned about the sensitivity of the mean to the presence of extreme values, which measure do you expect will change the most, the mean or the median?

126

Question 3.108

videogamesales

108. Recalculate the mean and the median of weekly sales, this time omitting Minecraft for PS3. Was your intuition in Exercise 107 confirmed?

Question 3.109

videogamesales

109. Compute the mean and median total sales for the 30 games.

Question 3.110

videogamesales

110. Identify the video game with the largest total sales. Omit this video game, and recompute the mean and median total sales. Which measure of center was more sensitive to the removal of the extreme value?

Question 3.111

videogamesales

111. Find the mode for each of the following variables:

  1. Platform
  2. Studio
  3. Game type

Question 3.112

videogamesales

112. Compute the mean, median, and mode for the variable weeks on list.

Question 3.113

videogamesales

image 113. What if we add a certain unknown amount to each value in the variable weeks on list? Describe what will happen to the following measures of center.

  1. Mean
  2. Median
  3. Mode