5 Probability

Section 5.4 Exercises

CLARIFYING THE CONCEPTS

Question 5.345

1. What type of diagram is helpful in itemizing the possible outcomes of a series of events? (p. 292)

5.4.1

Tree diagram

Question 5.346

2. Explain in words how is calculated. (p. 294)

Question 5.347

3. What is the difference between a permutation and a combination? (pp. 295–296)

5.4.3

In a permutation, order is important. In a combination, order is not important.

Question 5.348

4. Does make sense? Explain why or why not.(p. 295)

Question 5.349

5. Describe in your own words what is meant by acceptance sampling. (p. 300)

5.4.5

Answers will vary.

Question 5.350

6. The counting methods that we have learned in this section may be used to compute probabilities. (p. 301)

For assigning probability, which method is used:classical, relative frequency, or subjective?
Referring to part (a), what assumption must be made to apply the method?

PRACTICING THE TECHNIQUES

CHECK IT OUT!

To do	Check out	Topic
Exercises 7–10	Example 33	Tree diagrams
Exercises 11–12	Example 34	Counting with repetition
Exercises 13–14	Example 35	Counting without repetition
Exercises 15–16	Example 36	Traveling salesman problem, Part 1
Exercises 17–22	Example 37	Factorials
Exercises 23–24	Example 38	Traveling salesman problem, Part 2
Exercises 25–32	Example 39	Calculating numbers of permutations
Exercises 33–40	Example 42	Calculating numbers of combinations
Exercises 41–42	Example 45	Number of permutations of nondistinct items

Question 5.351

7. A pizza store offers the following options to its customers. Use a tree diagram to list all the possible options from which a customer may choose.

Cheese: no cheese, regular cheese, double cheese
Pepperoni: no pepperoni, regular pepperoni, double pepperoni

5.4.7

Question 5.352

8. An ice cream shop offers the following options to its customers. Use a tree diagram to list all the possible options from which a customer may choose.

Ice cream: vanilla, chocolate, mint chocolate chip
Toppings: hot fudge, butterscotch, sprinkles

Question 5.353

9. A particular baseball pitcher has to choose from the following options on each pitch. Use a tree diagram to list all the possible options.

Type of pitch: fastball, curve, slider
Horizontal position: inside corner, over the plate, outside corner
Vertical position: high, low

5.4.9

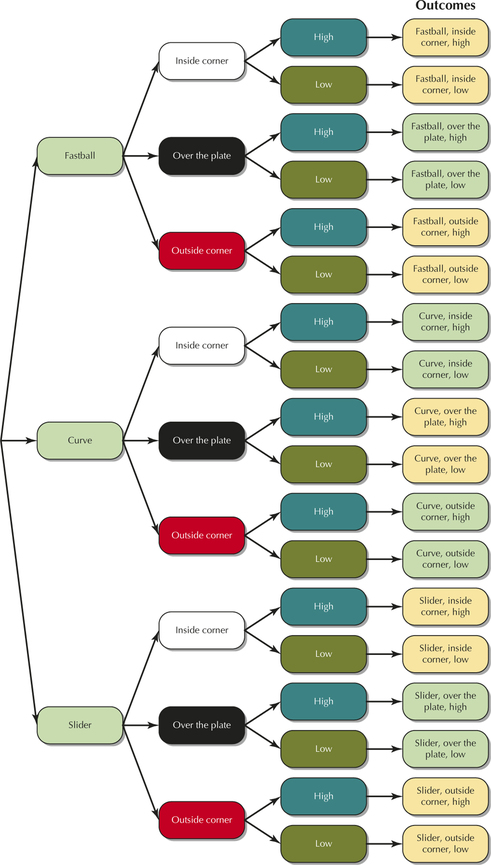
Question 5.354

10. A women's clothing store tracks its sales transactions according to the following options. Use a tree diagram to list all the possible options.

Payment method: credit card, debit card, check, cash
Size category: Juniors, Misses, Women's
Type of clothing: tops, pants

Question 5.355

11. Our 41st president, George Herbert Walker Bush, had four names, with initials GHWB. How many different possible sets of initials are there for people with four names?

5.4.11

26⁴

Question 5.356

12. NCAA ice hockey games can have the following outcomes: win (W), lose (L), or tie (T). In a tournament of five games, how many different possible sets of outcomes are there for a particular team? (Hint: LLTWW is one possible set.)

Question 5.357

13. A college dining service conducted a survey in which it asked students to select their first and second favorite flavors of ice cream from a list of five flavors: vanilla, chocolate, mint chocolate chip, strawberry, and maple walnut. How many different possible sets of two favorites are there?

5.4.13

Question 5.358

14. A town library is considering loaning video games, and surveyed its membership to ask their four favorite PlayStation 3 games from among the following six games: Gran Turismo, Call of Duty 4, Metal Gear Solid 4, Little Big Planet, Grand Theft Auto IV, and Final Fantasy XIII. How many different possible sets of four favorites are there?

304

Question 5.359

15. A woman is considering four sororities to rush this year. How many possible orderings are there?

5.4.15

Question 5.360

16. Students working for the college newspaper have six drop locations around campus at which they must drop off newspapers. How many different possible routes are there for the students to do so?

For Exercises 17–22, find the value of each factorial.

Question 5.361

17.

5.4.17

720

Question 5.362

18.

Question 5.363

19.

5.4.19

Question 5.364

20.

Question 5.365

21.

5.4.21

Question 5.366

22.

Question 5.367

23. A woman is considering four sororities to rush this year, but only has time to rush two. How many possible orderings are there?

5.4.23

Question 5.368

24. Students working for the college newspaper have six drop locations around campus at which they must drop off newspapers, but they only have enough time to get to four locations. How many different possible routes are there for the students to do so?

For Exercises 25–32, find the value of each permutation .

Question 5.369

25.

5.4.25

210

Question 5.370

26.

Question 5.371

27.

5.4.27

6720

Question 5.372

28.

Question 5.373

29.

5.4.29

100

Question 5.374

30.

Question 5.375

31.

5.4.31

93,326,215,443,944,152,681,699,238,856,266,700,490,715,968,264,381, 621,468,592,963,895,217,599,993,229,915,608,941,463,976,156,518,286,253, 697,920,827,223,758,251,185,210,916,864,000,000,000,000,000,000,000,000

Question 5.376

32.

For Exercises 33–40, find the value of each combination . Then answer Exercises 43 and 44.

Question 5.377

33.

5.4.33

Question 5.378

34.

Question 5.379

35.

5.4.35

165

Question 5.380

36.

Question 5.381

37.

5.4.37

Question 5.382

38.

Question 5.383

39.

5.4.39

Question 5.384

40.

Question 5.385

41. How many distinct strings of letters can we make by using all the letters in the word PIZZA?

5.4.41

5!/(2!1!1!1!) = 60

Question 5.386

42. How many distinct strings of letters can we make by using all the letters in the word PEPPERONI?

Question 5.387

43. Explain why the answers to Exercises 33 and 34 are equal. Use the commutative property of multiplication (for example, ) in your answer.

5.4.43

Question 5.388

44. Use the idea behind your answer to Exercise 43 to find a combination that is equal to . Verify your answer.

Question 5.389

45. List all the permutations of the following people taken three at a time: Amy, Bob, Chris, Danielle. What is ?

5.4.45

{Amy, Bob, Chris}, {Amy, Chris, Bob}, {Bob, Amy, Chris}, {Bob, Chris, Amy}, {Chris, Amy, Bob}, {Chris, Bob, Amy}, {Amy, Bob, Danielle}, {Amy, Danielle, Bob}, {Bob, Amy, Danielle}, {Bob, Danielle, Amy}, {Danielle, Amy, Bob}, {Danielle, Bob, Amy}, {Amy, Chris, Danielle}, {Amy, Danielle, Chris}, {Chris, Amy, Danielle}, {Chris, Danielle, Amy}, {Danielle, Amy, Chris}, {Danielle, Chris, Amy}, {Bob, Chris, Danielle}, {Bob, Danielle, Chris}, {Chris, Bob, Danielle}, {Chris, Danielle, Bob}, {Danielle, Bob, Chris}, {Danielle, Chris, Bob}.

Question 5.390

46. List all the combinations of the following people taken three at a time: Amy, Bob, Chris, Danielle. What is ?

Question 5.391

47. Explain in your own words why is larger than .

5.4.47

{Amy, Bob, Chris}, {Amy, Chris, Bob}, {Chris, Amy, Bob}, {Chris, Bob, Amy}, {Bob, Amy, Chris}, and {Bob, Chris, Amy} are all different permutations but the same combination.

Question 5.392

48. What quantity do we divide by to get ? Express this quantity as a factorial. (Hint: For example, if the quantity were 120, we would express it as )

Question 5.393

49. In general, what do we divide by to get ?

5.4.49

APPLYING THE CONCEPTS

Question 5.394

50. Fast Food. A fast-food restaurant has three types of sandwiches: chicken sandwich, fish sandwich, and beef burger. The restaurant has two types of side dishes: French fries and salad.

Draw a tree diagram to find all the different meals a customer can order at this restaurant.
How many different meals can a customer order at this restaurant?

Question 5.395

51. What to Eat? A sit-down restaurant has two types of appetizers: garden salad and Buffalo wings. It has threeentrees: spaghetti, steak, and chicken. And it offers three kinds of desserts: ice cream, cake, and pie.

Draw a tree diagram to find all the different meals a customer can order at this restaurant.
How many different meals can a customer order at this restaurant?

5.4.51

(a) See Solutions Manual. (b) 18

Question 5.396

52. Greek Alphabet. The ancient Greek alphabet had 24 letters. How many different possible initials are there forpeople with a first and last name?

Question 5.397

53. Facebook Friends. A student has 10 friends on her Facebook page. How many ways can she arrange her 10 friends top to bottom?

5.4.53

3,628,800

Question 5.398

54. Document Delivery. A document delivery person must deliver documents to five different destinations within aparticular city. How many different routes are possible?

Question 5.399

55. Traveler Fellow. A corporate sales executive must travel to the following countries this quarter: China, Russia, Germany, Brazil, India, and Nigeria. How many different routes are possible?

5.4.55

720

Question 5.400

56. Sales Traveler. A corporate sales executive has the choice of traveling to four of the following six countries this quarter: China, Russia, Germany, Brazil, India, and Nigeria. How many different routes are possible?

Question 5.401

57. Playing Catch. Five children are playing catch with a ball. How many different ways can one child throw a ball to another child once?

5.4.57

Question 5.402

58. Chimp Grooming. Six chimpanzees are grooming each other at the city zoo. In how many different ways can one chimp groom another?

Question 5.403

59. Shake Hands. In an ice-breaker exercise, each of 25 students is asked to shake hands with each of the other students. How many handshakes will there be in all?

5.4.59

300

Question 5.404

60. Statistics Competition. Three students from the Honors Statistics class of 15 students will be chosen to represent the school at the state statistics competition. How many differentpossible groupings of 3 students are there?

305

Question 5.405

61. How many random samples of size 1 can be chosen from a population of size 20?

5.4.61

Question 5.406

62. How many random samples of size 20 can be chosen from a population of size 20?

Question 5.407

63. How many random samples of size 10 can be chosen from a population of size 20?

5.4.63

184,756

Question 5.408

64. How many distinct strings of letters can be made using all the letters in the word MATHEMATICS?

Question 5.409

65. How many distinct strings of letters can be made using all the letters in the word BUSINESS?

5.4.65

6720

Question 5.410

66. Acceptance Sampling. A shipment of 25 personal digital assistants (PDAs) contains 3 that are defective.

A quality control specialist inspects 2 of the 25 PDAs. If both are defective, then the shipment is rejected.

Explain whether a permutation or a combination is being used.
Find the number of ways that both PDAs will be defective.
Find the probability of rejecting the shipment.