Chapter 6 Review Exercises
section 6.1
Question 6.423
1. Early Lunch. Chad has gotten to lunch early and is waiting for his friends to catch up. He figures that the probability that one friend shows up is 25%; two friends, 35%; three friends, 20%; and more than three friends, 5%.
- What is the probability that no friends show up?
- What is the probability that more than one friend shows up?
6.99.1
(a) 0.15 (b) 0.60
Question 6.424
2. Connecticut Lotto. The Connecticut Lottery Corporation runs a game called Connecticut Classic Lotto. The player picks six different numbers from 1 to 44 and pays $1 to play.
- If your picks match 3 of the 6 numbers chosen (probability 0.02381), you win $2.
- If you match 4 out of 6 (probability 0.001495), you win $50.
- If you match 5 out of 6 (probability 0.0000323), you win $2000.
- If you match all 6 numbers (probability 0.0000001417), you win the jackpot. The jackpot on March 17, 2015, was $1,500,000.
- Construct the probability distribution of your winnings. Make sure to include the probability of not winning anything (in effect, losing $1), which equals 1 minus the sum of the four probabilities specified above.
- Find the expected winnings. Compare this with the price to play.
section 6.2
Question 6.425
3. Gestational Diabetes. Gestational diabetes occurs in 8% of pregnancies, according to the American Diabetes Association. A random sample of 20 pregnancies is taken.
- Find the probability that none of the pregnancies results in gestational diabetes.
- Find the probability that at least one of the pregnancies results in gestational diabetes.
- Find the probability that at most two of the pregnancies result in gestational diabetes.
6.99.3
(a) 0.1887 (b) 0.8113 (c) 0.7880
Question 6.426
4. Price of Gas. The Pew Research Center reports that, in March 2011, 90% of Americans said they were hearing mostly bad news about the price of gasoline. A random sample of 15 Americans is taken.
- Find the probability that 12 Americans said that they were hearing mostly bad news about the price of gas.
- Find the probability that between 12 and 14 Americans inclusive said that they were hearing mostly bad news about the price of gas.
- Find the mean, variance, and standard deviation of the number of Americans. Interpret the mean.
section 6.3
For each of the following situations, assume that the requirements for the Poisson probability distribution are met.
Use the mean to find the indicated probability.
Question 6.427
5. μ=5; find P(X=5)
6.99.5
0.1755
Question 6.428
6. μ=5; find P(3≤X≤5)
Question 6.429
7. μ=5; find P(X<3)
6.99.7
0.1247
Question 6.430
8. μ=5; find P(0≤X≤5)
Question 6.431
9. Aircraft Fatalities. The mean number of fatalities per crash of small aircraft in California is 1.65. Let X refer to the number of fatalities per crash. Find the following probabilities:
- Probability that X=1
- P(X=0)
- P(X≤2)
- P(X>2)
(Source: Aviation Accident Data and Synopses, National Transportation Safety Board, 2014, http://www.ntsb.gov/_layouts/ntsb.aviation/index.aspx.)
6.99.9
(a) 0.3169 (b) 0.1920 (c) 0.7703 (d) 0.2297
section 6.4
Systolic Blood Pressure. Use the following information for Exercises 10–13. A study found that the mean systolic blood pressure was 106 mm Hg.21 Assume that systolic blood pressure follows a normal distribution with mean μ=106 and standard deviation σ=8.
Question 6.432
10. What is the probability that a randomly chosen systolic blood pressure is equal to 106 mm Hg?
Question 6.433
11. What is the probability that a randomly selected systolic blood pressure is more than 106 mm Hg?
6.99.11
0.5
Question 6.434
12. Is the area to the right of X=110 mm Hg greater than or less than 0.5? How do you know this?
Question 6.435
13. What is the probability that a randomly selected systolic blood pressure is between 98 and 114 mm Hg?
6.99.13
About 0.68
For Exercises 14–19, (a) draw the graph, and (b) find the indicated area using the Z table or technology.
Find the area under the standard normal curve that lies to the left of the following:
Question 6.436
14. Z=2.1
Question 6.437
15. Z=2.9
6.99.15
(a)

(b) 0.9981
Find the area under the standard normal curve that lies to the right of the following:
Question 6.438
16. Z=−2.2
Question 6.439
17. Z=−2.9
6.99.17
(a)

(b) 0.9981
Find the area under the standard normal curve that lies between the following:
Question 6.440
18. Z=−1.28 and Z=1.28
Question 6.441
19. Z=−1.04 and Z=1.51
6.99.19
(a)
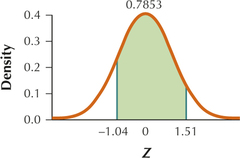
(b) 0.7853
section 6.5
Question 6.442
20.Drunk-Driving Deaths. in the United States, a mean of 48 people per day are killed in vehicle accidents involving a drunk driver. Assume that the distribution of drunk-driving accident deaths per day is normal, μ=48, and σ=12.
- Find the probability that, at most, 12 people will be killed in drunk-driving accidents today.
- Find the probability that between 50 and 80 people will be killed in drunk-driving accidents today.
- Find the 99.5th percentile of the number of drunk-driving accident deaths.
- Suppose on one particular day in the United States, 60 people are killed in drunk-driving accidents. Is this unusual? On what do you base your answer?
Question 6.443
21.Math Scores. The National Assessment for Educational Progress reports that mean scores on the standardized math test for eighth-graders in 2013 was μ=153
σ=10
.- Find the probability that the test score of a randomly selected eighth-grader was greater than 178.
- What proportion of test scores was between 153 and 178?
- Suppose students who scored at the 5th percentile or lower could not graduate. Find the 5th percentile test score.
- Suppose you know someone who scored 188 on the test. Is this unusual? On what do you base your answer?
6.99.21
(a) 0.0062 (b) 0.4938 (c) 136.55 (d) Yes; z-score=3.5≥3.
section 6.6
Question 6.444
22.Reinstate the Draft? A New York Times/CBS News Poll found that 97% of young Americans (ages 17–29) oppose reinstating the military draft. Suppose we take a random sample of 400 young Americans. Use the normal approximation to approximate the following probabilities:
- Exactly 388 oppose reinstating the military draft.
- All 400 oppose reinstating the military draft.
- More than 388 oppose reinstating the military draft.
- At most 388 oppose reinstating the military draft.
- Fewer than 388 oppose reinstating the military draft.
- Between 385 and 390 (inclusive) oppose reinstating the military draft.