9 Hypothesis Testing

Chapter 9 Review Exercises

section 9.1

For Exercises 1–3, provide the null and alternative hypotheses.

Question 9.386

1. Test whether $μ < 12$ .

9.99.1

$H_{0} : μ = 12 vs . H_{a} : μ < 12$

Question 9.387

2. Test whether $μ > 10$ .

Question 9.388

3. Test whether $μ$ is below zero.

9.99.3

$H_{0} : μ = 0 vs . H_{a} : μ < 0$

For Exercises 4–6, do the following.

Provide the null and alternative hypotheses.
Describe the two ways a correct decision could be made.
Describe what a Type I error would mean in the context of the problem.
Describe what a Type II error would mean in the context of the problem.

Question 9.389

4. Household Size. The U.S. Census Bureau reported (2010) that the mean household size is 2.58 persons. We conduct a hypothesis test to determine whether the population mean household size has changed.

Question 9.390

5. Speeding-Related Traffic Fatalities. The National Highway Traffic Safety Administration reports that the mean number of speeding-related traffic fatalities over the Thanksgiving holiday period from 1994 to 2003 was 202.7. We conduct a hypothesis test to examine whether the population mean number of such fatalities has decreased.

9.99.5

(a) $H_{0} : μ = 202.7 vs . H_{a} : μ < 202.7$ (b) We conclude that (1) the population mean number of speeding-related fatalities is less than 202.7 when it actually is and (2) the mean number of speeding-related fatalities is not less than 202.7 when it actually is. (c) The population mean number of speeding-related fatalities is less than 202.7 when it actually is not less than 202.7. (d) The population mean number of speeding-related fatalities is not less than 202.7 when it actually is less than 202.7.

Question 9.391

6. Salaries of Accounting Associate Professors. Salary.com reports that the mean salary for accounting associate professors in 2014 was $94,000. A hypothesis test was conducted to determine if the population mean salary of accounting associate professors has increased.

section 9.2

For Exercises 7–9, find the value of $Z_{data}$ .

Question 9.392

7. $\bar{x} = 59, σ = 10, n = 100, μ_{0} = 60$

9.99.7

–1

Question 9.393

8. $\bar{x} = 59, σ = 5, n = 100, μ_{0} = 60$

Question 9.394

9. $\bar{x} = 59, σ = 1, n = 100, μ_{0} = 60$

9.99.9

–10

For each of the following hypothesis tests in Exercises 10–12, do the following:

Find the value of $Z_{data}$ .
Find the critical-value rejection rule.
Draw a standard normal curve and indicate the critical region.
State the conclusion and interpretation.

Question 9.395

10. $H_{0} : μ = μ_{0} vs . H_{a} : μ \neq μ_{0}, α = 0.01, Z_{data} = - 2.5$

Question 9.396

11. $H_{0} : μ = μ_{0} vs . H_{a} : μ > μ_{0}, α = 0.10, Z_{data} = 1.5$

9.99.11

(a) 1.28 (b) Reject $H_{0}$ if $Z_{data} \geq 1.28$ .

(c)

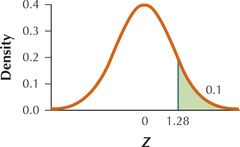
(d) Since $Z_{data} \geq 1.28$ , we reject $H_{0}$ . There is evidence that the population mean is greater than $μ_{0}$ .

Question 9.397

12. $H_{0} : μ = μ_{0} vs . H_{a} : μ > μ_{0}, α = 0.05, Z_{data} = - 2.5$

Question 9.398

13. Credit Scores in Georgia. According to CreditReport. com, the mean credit score in Georgia in 2014 was 668. A random sample of 144 Georgia residents this year shows a mean credit score of 650. Assume $a = 50$ . Perform a hypothesis test, using level of significance $α = 0.05$ , to determine if the population mean credit score in Georgia has decreased.

State the hypotheses.
Find the value of $Z_{crit}$ and the rejection rule. Also, draw a standard normal curve, indicating the critical region.
Calculate $Z_{data}$ . Draw a standard normal curve showing $Z_{crit}$ , the critical region, and $Z_{data}$ .
State the conclusion and the interpretation.

9.99.13

(a) $H_{0} : μ = 668 vs . H_{a} : μ < 668$ –(b) −1.645; reject $H_{0}$ if $Z_{data} \leq - 1.645$ (c) $Z_{data} = - 4.32$

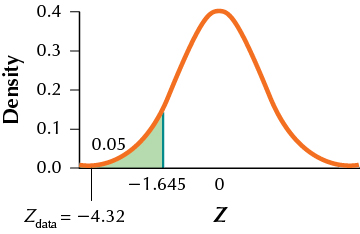
(d) Since $Z_{data} \leq - 1.645$ , we reject $H_{0}$ . There is evidence that the population mean credit score in Georgia is less than 668.

section 9.3

For Exercises 14 and 15, perform the following steps:

State the hypotheses and the rejection rule for the $p$ -value method.
Calculate $Z_{data}$ .
Find the $p$ -value. Draw the standard normal curve, with $Z_{data}$ and the $p$ -value indicated on it.
State the conclusion and the interpretation.

Question 9.399

14. We are interested in testing at level of significance $α = 0.05$ whether the population mean differs from 500. A random sample of size 100 is taken, with a mean of 520. Assume $σ = 50$ .

Question 9.400

15. We want to test, at level of significance $α = 0.01$ , whether the population mean is less than −10. A random sample of size 25 is taken from a normal population. The sample mean is −12. Assume $σ = 2$ .

9.99.15

(a) $H_{0} : μ = - 10 vs . H_{0} : μ < - 10$ . Reject $H_{0}$ if the $p -value \leq 0.01$ . (b) −5 (c) $p -value = 2.87105 \times 10^{- 7}$

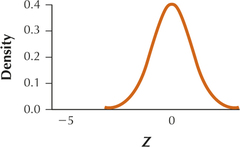
(d) Since the $p -value \leq 0.01$ , reject $H_{0}$ . There is evidence that the population mean is less than −10.

Question 9.401

16. Sleeping During the Full Moon. A study found that subjects slept on average 20 minutes less on nights of the full moon than otherwise.²¹ Other researchers disagree and are interested in testing whether the mean difference in sleep is less than 20 minutes. A random sample of 100 subjects showed that they slept, on average, 10 minutes less on nights of the full moon than otherwise. Assume the population standard deviation is 15 minutes. Perform the appropriate hypothesis test using level of significance $α = 0.01$ .

section 9.4

For Exercises 17–19, find the critical value $t_{crit}$ and sketch the critical region. Assume normality.

Question 9.402

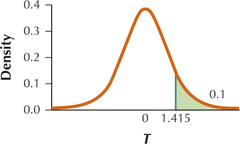
17. $H_{0} : μ = 100, H_{a} : μ > 100, n = 8, α = 0.10$

9.99.17

$t_{crit} = 1.415$

Question 9.403

18. $H_{0} : μ = 100, H_{a} : μ > 100, n = 8, α = 0.05$

Question 9.404

19. $H_{0} : μ = 100, H_{a} : μ > 100, n = 8, α = 0.01$

9.99.19

$t_{crit} = 2.998$

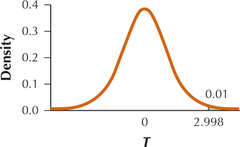
Question 9.405

20. Describe what happens to the $t$ critical value $t_{crit}$ for right-tailed tests as $α$ decreases.

Question 9.406

21. A random sample of size 16 from a normal population yields a sample mean of 10 and a sample standard deviation of 3. Test whether the population mean differs from 9, using level of significance $α = 0.10$ .

9.99.21

$H_{0} : μ = 9 vs . H_{0} : μ \neq 9$ . $t_{crit} = 1.753$ . Reject $H_{0}$ if $t_{data} \leq - 1.753$ or $t_{data} \geq 1.753$ . Since $t_{data}$ is not $\leq - 1.753$ and $t_{data}$ is not $\geq 1.753$ we do not reject $H_{0}$ . There is insufficient evidence that the population mean is different from 9.

Question 9.407

22. A random sample of size 144 from an unknown population yields a sample mean of 45 and a sample standard deviation of 10. Test whether the population mean differs from 45, using level of significance $α = 0.10$ .

section 9.5

For Exercises 23–25, do the following:

Check the normality conditions.
State the hypotheses.
Find $Z_{crit}$ and the rejection rule.
Calculate $Z_{data}$ .
State the conclusion and the interpretation.

Page 572

Question 9.408

23. Test whether the population proportion exceeds 0.8. A random sample of size 1000 yields 830 successes. Let $α = 0.10$ .

9.99.23

(a) We have $n p_{0} = 100 (0.8) = 800 \geq 5$ and $n (1 - p_{0}) = 1000 (1 - 0.8) = 200 \geq 5$ . (b) $H_{0} : p = 0.8 vs . H_{0} : p > 0.8$ (c) $Z_{crit} = 1.28$ . Reject $H_{0}$ if $Z_{data} \geq 1.28$ . (d) $Z_{data} = 2.37$ (e) Since $Z_{data} \geq 1.28$ , we reject $H_{0}$ . There is evidence that the population proportion is greater than 0.8.

Question 9.409

24. Test whether the population proportion is below 0.2. A random sample of size 900 yields 160 successes. Let $α = 0.05$ .

Question 9.410

25. Test whether the population proportion is not equal to 0.4. A random sample of size 100 yields 55 successes. Let $α = 0.01$ . For Exercises 26 and 27, do the following:

Check the normality conditions.
State the hypotheses and the rejection rule for the $p$ -value method, using level of significance $α = 0.05$ .
Calculate $Z_{data}$ .
Calculate the $p$ -value.
State the conclusion and the interpretation.

9.99.25

(a) We have $n p_{0} = 100 (0.4) = 40 \geq 5$ and $n (1 - p_{0}) = 100 (1 - 0.4) = 60 \geq 5$ . (b) $H_{0} : p = 0.4 vs . H_{a} : p \neq 0.4$ (c) $Z_{crit} = 2.58$ . Reject $H_{0}$ if $Z_{data} \leq - 2.58$ or $Z_{data} \geq 2.58$ . (d) $Z_{data} = 3.06$ (e) Since $Z_{data} \geq 2.58$ , we reject $H_{0}$ . There is evidence that the population proportion is not equal to 0.4.

Question 9.411

26. Test whether the population proportion differs from 0.7. A random sample of size 144 yields 110 successes.

Question 9.412

27. Test whether the population proportion is less than 0.25. A random sample of size 100 yields 25 successes.

9.99.27

(a) We have $n p_{0} = 100 (0.25) = 25 \geq 5$ and $n (1 - p_{0}) = 100 (1 - 0.25) = 75 \geq 5$ . (b) $H_{0} : p = 0.25 vs . H_{^{α}} : p < 0.25$ . Reject $H_{0}$ if the $p -value \leq 0.05$ . (c) 0 (d) 0.5 (e) Since the $p -value$ is not $\leq 0.05$ , we do not reject $H_{0}$ . There is insufficient evidence that the population proportion is less than 0.25.

Question 9.413

28. DSL Internet Service. The U.S. Department of Commerce reports that 41.6% of Internet users preferred DSL as their method of service delivery.²² A random sample of 1000 Internet users shows 350 who preferred DSL. If appropriate, test whether the population proportion who prefer DSL has decreased, using level of significance $α = 0.05$ .

section 9.6

For Exercises 29 and 30, assume normality of the data, and do the following:

State the hypotheses.
Find the $χ^{2}$ critical value or values, and state the rejection rule.
Find $χ_{data}^{2}$ . Also, draw a $χ^{2}$ distribution and indicate $χ_{data}^{2}$ and the $χ^{2}$ critical value or values.
State the conclusion and the interpretation.

Question 9.414

29. We are testing whether $σ > 6$ and have a random sample of size 20 with a standard deviation of $s = 9$ . Let $α = 0.05$ .

9.99.29

(a) $H_{0} : σ = 6 vs . H_{a} : σ > 6$ (b) $χ_{a}^{2} = χ_{0 .05}^{2} = 30.144$ . Reject $H_{0}$ if $χ_{data}^{2} \geq 30.144$ . (c) $χ_{data}^{2} = 42.75$

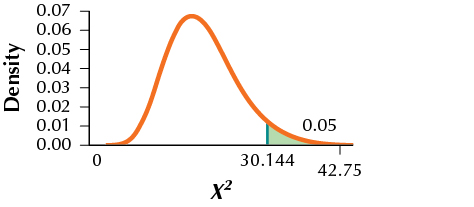
(d) Since $χ_{data}^{2} \geq 30.144$ , we reject $H_{0}$ . There is evidence that the population standard deviation is greater than 6.

Question 9.415

30. We are testing whether $σ \neq 10$ and have a random sample of size 26 with a sample variance of 90. Let $α = 0.05$ .

For Exercises 31 and 32, assume normality of the data, and do the following:

State the hypotheses and the $p$ -value rejection rule for $α = 0.05$ .
Find $χ_{data}^{2}$ .
Find the $p$ -value. Also, draw a $χ^{2}$ distribution and indicate $χ_{data}^{2}$ and the $p$ -value.
State the conclusion and the interpretation.

Question 9.416

31. We are testing whether $σ < 35$ and have a random sample of size eight with a sample variance of 1200.

9.99.31

(a) $H_{0} : σ = 35 vs . H_{a} : σ < 35$ . Reject $H_{0}$ if the $p -value \leq 0.05$ . (b) 6.857 (c) $p -value = 0.5560805474$

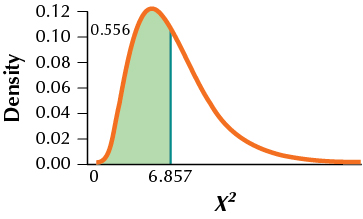
(d) Since the $p -value$ is not $\leq 0.05$ , we do not reject $H_{0}$ . There is insufficient evidence that the population standard deviation is less than 35.

Question 9.417

32. We are testing whether $σ \neq 50$ and have a random sample of size 26 with a standard deviation of $s = 45$ .

section 9.7

For Exercises 33–38, assume that the conditions for performing the $Z$ test are met. Do the following:

Calculate the value or values of ${\bar{x}}_{crit}$ .
Draw a normal curve, centered at $μ_{a}$ , with the value or values of ${\bar{x}}_{crit}$ indicated.
Calculate $β$ , the probability of a Type II error for that value of $μ_{a}$ . Shade the corresponding area under the normal curve.
Calculate the power of the hypothesis test.

Question 9.418

33. $H_{0} : μ = 100 vs . H_{a} : μ \neq 100, α = 0.01, σ = 15, n = 64, μ_{a} = 103$

9.99.33

(a) ${\bar{x}}_{critical, lower} = 95.1625$ , ${\bar{x}}_{critical, upper} = 104.8375$

(b)

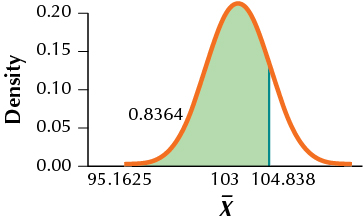
(c) TI-83/84: 0.8364 (d) 0.1636

Question 9.419

34. $H_{0} : μ = 100 vs . H_{a} : μ \neq 100, α = 0.01, σ = 15, n = 64, μ_{a} = 106$

Question 9.420

35. $H_{0} : μ = 100 vs . H_{a} : μ \neq 100, α = 0.01, σ = 15, n = 64, μ_{a} = 109$

9.99.35

(a) ${\bar{x}}_{critical, lower} = 95.1625$ , ${\bar{x}}_{critical, upper} = 104.8375$

(b)

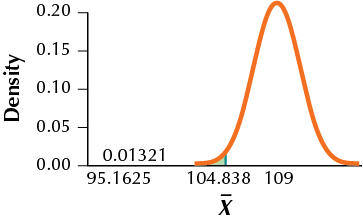
(c) TI-83/84: 0.0132 (d) 0.9868

Question 9.421

36. $H_{0} : μ = 100 vs . H_{a} : μ \neq 100, α = 0.01, σ = 15, n = 64, μ_{a} = 112$

Question 9.422

37. $H_{0} : μ = 100 vs . H_{a} : μ \neq 100, α = 0.01, σ = 15, n = 64, μ_{a} = 115$

9.99.37

(a) ${\bar{x}}_{critical, lower} = 95.1625$ , ${\bar{x}}_{critical, upper} = 104.8375$

(b)

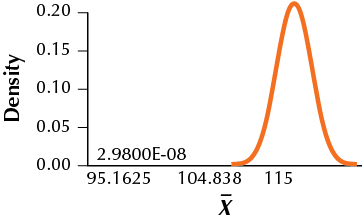
(c) 0 (d) 1

Question 9.423

38. Refer to Exercises 33–37. Construct the power curve for the given values of $μ_{a}$ .