KEY THEME

Problem solving refers to thinking and behavior directed toward attaining a goal that is not readily available.

KEY QUESTIONS

From fixing flat tires to figuring out how to pay for college classes, we engage in the cognitive task of problem solving so routinely that we often don’t even notice the processes we follow. Formally, problem solving refers to thinking and behavior directed toward attaining a goal that is not readily available (Novick & Bassok, 2005; Wang & Chiew, 2010).

Before you can solve a problem, you must develop an accurate understanding of the problem. Correctly identifying the problem is a key step in successful problem solving (Bransford & Stein, 1993). If your representation of the problem is flawed, your attempts to solve it will also be flawed.

As a general rule, people tend to attack a problem in an organized or systematic way. Usually, the strategy you select is influenced by the nature of the problem and your degree of experience, familiarity, and knowledge about the problem you are confronting (Chrysikou, 2006; Leighton & Sternberg, 2013). In this section, we’ll look at some of the common strategies used in problem solving.

TRIAL AND ERROR

A PROCESS OF ELIMINATION

The strategy of trial and error involves actually trying a variety of solutions and eliminating those that don’t work. When there is a limited range of possible solutions, trial and error can be a useful problem-solving strategy. If you were trying to develop a new spaghetti sauce recipe, for example, you might use trial and error to fine-tune the seasonings.

When the range of possible answers or solutions is large, however, trial and error can be very time-consuming. For example, your author Sandy has a cousin who hates reading written directions, especially for projects like assembling Ikea furniture or making minor household repairs. Rather than taking the time to read through the directions, he’ll spend hours trying to figure out how the pieces fit together.

278

ALGORITHMS

GUARANTEED TO WORK

Unlike trial and error, an algorithm is a procedure or method that, when followed step by step, always produces the correct solution. Mathematical formulas are examples of algorithms. For instance, the formula used to convert temperatures from Celsius to Fahrenheit (multiply C by 9/5, then add 32) is an algorithm.

Even though an algorithm may be guaranteed to eventually produce a solution, using an algorithm is not always practical. For example, imagine that while rummaging in a closet you find a combination lock with no combination attached. Using an algorithm will eventually produce the correct combination. You can start with 0–0–0, then try 0–0–1, followed by 0–0–2, and so forth, and systematically work your way through combinations to 36–36–36. But this solution would take a while, because there are 46,656 potential combinations to try. So, although using an algorithm to generate the correct combination for the combination lock is guaranteed to work eventually, it’s not a very practical approach to solving this particular problem.

HEURISTICS

RULES OF THUMB

In contrast to an algorithm, a heuristic is a general rule-of-thumb strategy that may or may not work. Although heuristic strategies are not guaranteed to solve a given problem, they tend to simplify problem solving because they let you reduce the number of possible solutions. With a more limited range of solutions, you can use trial and error to eventually arrive at the correct one. In this way, heuristics may serve an adaptive purpose by allowing us to use patterns of information to solve problems quickly and accurately (Gigerenzer & Gaissmeier, 2011; Gigerenzer & Goldstein, 2011).

Here’s an example. Creating footnotes is described somewhere in the onscreen “Help” documentation for a word-processing software program. If you use the algorithm of scrolling through every page of the Help program, you’re guaranteed to solve the problem eventually. But you can greatly simplify your task by using the heuristic of entering “footnotes” in the Help program’s search box. This strategy does not guarantee success, however, because the search term may not be indexed.

One common heuristic is to break a problem into a series of subgoals. This strategy is often used in writing a term paper. Choosing a topic, locating information about the topic, organizing the information, and so on become a series of subproblems. As you solve each subproblem, you move closer to solving the larger problem. Another useful heuristic involves working backward from the goal. Starting with the end point, you determine the steps necessary to reach your final goal. For example, when making a budget, people often start off with the goal of spending no more than a certain total each month, then work backward to determine how much of the target amount they will allot for each category of expenses.

Perhaps the key to successful problem solving is flexibility. A good problem solver is able to recognize that a particular strategy is unlikely to yield a solution—and knows to switch to a different approach (Bilalić & others, 2008; Ionescu, 2012). And, sometimes, the reality is that a problem may not have a single “best” solution.

Remember Tom, whose story we told in the Prologue? One characteristic of many people with autism spectrum disorder is cognitive rigidity and inflexible thinking (Kleinhans & others, 2005; Leung & Zakzanis, 2014; Toth & King, 2008). Like Tom, many people can become frustrated when they are “stuck” on a problem. Unlike Tom, most people are able to sense when it’s time to switch to a new strategy, take a break for a few hours, seek assistance from experts or others who may be more knowledgeable—or accept defeat and give up. In Tom’s case, rather than give up on a problem or seek a different approach to solving it, Tom will persevere in his attempt to solve it. For example, faced with a difficult homework problem in an advanced mathematics class, Tom often stayed up until 2:00 or 3:00 A.M., struggling to solve a single problem until he literally fell asleep at his desk.

279

Similarly, successful problem solving sometimes involves accepting a less-than-perfect solution to a particular problem—knowing when a solution is “good enough,” even if not perfect. But to many with autism spectrum disorder, things are either right or wrong—there is no middle ground (Toth & King, 2008). So when Tom got a 98 rather than 100 on a difficult math test, he was inconsolable. When he ranked in the top five in his class, he was upset because he wasn’t first. Tom would sometimes be unable to write an essay because he couldn’t think of a perfect opening sentence, or turn in an incomplete essay because he couldn’t think of the perfect closing sentence.

INSIGHT AND INTUITION

The solution to some problems seems to arrive in a sudden realization, or flash of insight, that happens after you mull a problem over (Ohlsson, 2010; Öllinger & others, 2008). Sometimes an insight will occur when you recognize how the problem is similar to a previously solved problem. Or an insight can involve the sudden realization that an object can be used in a novel way. Try your hand at the two problems in Figure 7.3. The solution to each of those problems is often achieved by insight.

Insights rarely occur through the conscious manipulation of concepts or information. In fact, you’re usually not aware of the thought processes that lead to an insight. Increasingly, cognitive psychologists and neuroscientists are investigating nonconscious processes, including unconscious problem solving, insight, and intuition (Hogarth, 2010; Horr & others, 2014). Intuition means coming to a conclusion or making a judgment without conscious awareness of the thought processes involved.

One influential model of intuition is the two-stage model (Bowers & others, 1990; Hodgkinson & others, 2008). In the first stage, called the guiding stage, you perceive a pattern in the information you’re considering, but not consciously. The perception of such patterns is based on your expertise in a given area and your memories of related information.

In the second stage, the integrative stage, a representation of the pattern becomes conscious, usually in the form of a hunch or hypothesis. At this point, conscious analytic thought processes take over. You systematically attempt to prove or disprove the hypothesis. For example, an experienced doctor might integrate both obvious and subtle cues to recognize a pattern in a patient’s symptoms, a pattern that takes the form of a hunch or an educated guess. Once the hunch is consciously formulated, she might order lab tests to confirm or disprove her tentative diagnosis.

An intuitive hunch, then, is a new idea that integrates new information with existing knowledge stored in long-term memory. Such hunches are likely to be accurate only in contexts in which you already have a broad base of knowledge and experience (Jones, 2003; M. Lieberman, 2000).

280

THINKING OUTSIDE THE BOX

Sometimes, past experience or expertise in a particular domain can actually interfere with effective problem solving. If we’re used to always doing something in a particular way, we may not be open to new or better solutions. When we can’t move beyond old, inappropriate heuristics, ideas, or problem-solving strategies, fixation can block the generation of new, more effective approaches (Moss & others, 2011; Storm & Angello, 2010).

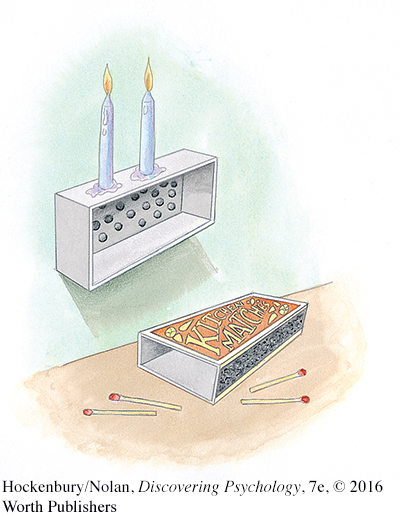
When we view objects as functioning only in the usual or customary way, we’re engaging in a tendency called functional fixedness. Functional fixedness often prevents us from seeing the full range of ways in which an object can be used. To get a feel for how functional fixedness can interfere with your ability to find a solution, try the problem in Figure 7.4.

For example, consider the problem of disposing of plastic bags, which take decades to centuries to degrade and clog landfills and waterways. Hundreds of U.S. cities have dealt with the problem by passing ordinances banning or restricting their use. Functional fixedness kept people from thinking of the bags as anything but trash. But it turns out that the indestructible nature of these single-use bags can be advantageous: the bags can be turned into “plarn,” a plastic yarn that can be repurposed to create durable, waterproof sleeping mats for the homeless. A Chicago-based group, New Life for Old Bags, estimates that it takes between 600 and 700 plastic bags to create one six-by-two foot sleeping mat. The finished mats are distributed to homeless shelters throughout the city (Stuart, 2013).

Another common obstacle to problem solving is mental set—the tendency to persist in solving problems with solutions that have worked in the past (Öllinger & others, 2008). Obviously, if a solution has worked in the past, there’s good reason to consider using it again. However, if we approach a problem with a rigid mental set, we may not see other possible solutions (Kershaw & Ohlsson, 2004).

Ironically, mental set is sometimes most likely to block insight in areas in which you are already knowledgeable or well trained. Before you read any further, try solving the simple arithmetic problems in Figure 7.5. If you’re having trouble coming up with the answer, it’s probably because your existing training in solving arithmetic problems is preventing you from seeing the equations from a different perspective than what you have been taught (Knoblich & Öllinger, 2006; Öllinger & others, 2008).

Mental sets can sometimes suggest a useful heuristic. But they can also prevent us from coming up with new, and possibly more effective, solutions. If we try to be flexible in our thinking and overcome the tendency toward mental sets, we can often identify simpler solutions to many common problems.

281

KEY THEME

Different cognitive strategies are used when making decisions, depending on the type and number of options available to us.

KEY QUESTIONS

Who hasn’t felt like flipping a coin when faced with an important or complicated decision? Fortunately, most of the decisions we make in everyday life are relatively minor. But every now and then we have to make a decision where much more is at stake. When a decision is important or complex, we’re more likely to invest time, effort, and other resources in considering different options.

The decision-making process becomes complicated when each option involves the consideration of several features. It’s rare that one alternative is superior in every category. So, what do you do when each alternative has pros and cons? In this section, we’ll describe three common decision-making strategies.

THE SINGLE-FEATURE MODEL

One decision-making strategy is called the single-feature model. In order to simplify the choice among many alternatives, you base your decision on a single feature. When the decision is a minor one, the single-feature model can be a good decision-making strategy. For example, faced with an entire supermarket aisle of laundry detergents, you could simplify your decision by deciding to buy the cheapest brand. When a decision is important or complex, however, making decisions on the basis of a single feature can increase the riskiness of the decision.

THE ADDITIVE MODEL

A better strategy for complex decisions is to systematically evaluate the important features of each alternative. One such decision-making model is called the additive model.

In this model, you first generate a list of the factors that are most important to you. For example, suppose you need off-campus housing. Your list of important factors might include cost, proximity to campus, compatibility with roommates, or having a private bathroom. Then, you rate each alternative for each factor using an arbitrary scale, such as from –5 to +5. If a particular factor has strong advantages or appeal, such as compatible roommates, you give it the maximum rating (+5). If a particular factor has strong drawbacks or disadvantages, such as distance from campus, you give it the minimum rating (–5). Finally, you add up the ratings for each alternative. This strategy can often reveal the best overall choice. If the decision involves a situation in which some factors are more important than others, you can emphasize the more important factors by multiplying the rating.

Taking the time to apply the additive model to important decisions can greatly improve your decision making. By allowing you to evaluate the features of one alternative at a time, then comparing the alternatives, the additive model provides a logical strategy for identifying the most acceptable choice from a range of possible decisions. Although we seldom formally calculate the subjective value of individual features for different options, we often informally use the additive model by comparing two choices feature by feature. The alternative with the “best” collection of features is then selected.

282

THE ELIMINATION-BY-ASPECTS MODEL

Psychologist Amos Tversky (1972) proposed another decision-making model called the elimination-by-aspects model. Using this model, you evaluate all of the alternatives one characteristic at a time, typically starting with the feature you consider most important. If a particular alternative fails to meet that criterion, you scratch it off your list of possible choices, even if it possesses other desirable attributes. As the range of possible choices is narrowed down, you continue to compare the remaining alternatives, one feature at a time, until just one alternative is left.

For example, suppose you want to buy a new laptop. You might initially eliminate all the models that aren’t powerful enough to run the software you need to use, then the models outside your budget, and so forth. Continuing in this fashion, you would progressively narrow down the range of possible choices to the one choice that satisfies all your criteria.

Good decision makers adapt their strategy to the demands of the specific situation. If there are just a few choices and features to compare, people tend to use the additive method, at least informally. However, when the decision is complex, involving the comparison of many choices that have multiple features, people often use more than one strategy. That is, we usually begin by focusing on the critical features, using the elimination-by-aspects strategy to quickly narrow down the range of acceptable choices. Once we have narrowed the list of choices down to a more manageable short list, we tend to use the additive model to make a final decision. Of course, it’s not always as straightforward as this. Other factors, such as our emotions, play in to our decision making, too (Lerner & others, 2015).

ESTIMATING THE PROBABILITY OF EVENTS

Some decisions involve a high degree of uncertainty. In these cases, you need to make a decision, but you are unable to predict with certainty that a given event will occur. Instead, you have to estimate the probability of an event occurring. But how do you actually make that estimation?

For example, imagine that you’re running late for a very important appointment. You may be faced with this decision: “Should I risk a speeding ticket to get to the appointment on time?” In this case, you would have to estimate the probability of a particular event occurring—getting pulled over for speeding.

In such instances, we often estimate the likelihood that certain events will occur, then gamble. In deciding what the odds are that a particular gamble will go our way, we tend to rely on two rule-of-thumb strategies to help us estimate the likelihood of events: the availability heuristic and the representativeness heuristic (Tversky & Kahneman, 1982; Kahneman, 2003).

THE AVAILABILITY HEURISTIC

When we use the availability heuristic, we estimate the likelihood of an event on the basis of how readily available other instances of the event are in our memory. When instances of an event are easily recalled, we tend to consider the event as being more likely to occur. So, we’re less likely to exceed the speed limit if we can readily recall that a friend recently got a speeding ticket.

283

However, when a rare event makes a vivid impression on us, we may overestimate its likelihood (Tversky & Kahneman, 1982). State lottery commissions capitalize on this cognitive tendency by running many TV commercials showing that lucky person who won the $100 million Powerball. A vivid memory is created, which leads viewers to an inaccurate estimate of the likelihood that the event will happen to them.

The key point here is that the less accurately our memory of an event reflects the actual frequency of the event, the less accurate our estimate of the event’s likelihood will be. That’s why the lottery commercials don’t show the other 50 million people staring dejectedly at their TV screens because they did not win the $100 million.

THE REPRESENTATIVENESS HEURISTIC

The other heuristic we often use to make estimates is called the representativeness heuristic (Kahneman & Tversky, 1982; Kahneman, 2003). Here, we estimate an event’s likelihood by comparing how similar its essential features are to our prototype of the event. Remember, a prototype is the most typical example of an object or an event.

To go back to our example of deciding whether to speed, we are more likely to risk speeding if we think that we’re somehow significantly different from the prototype of the driver who gets a speeding ticket. If our prototype of a speeder is a teenager driving a flashy, high-performance car, and we’re an adult driving a minivan with a baby seat, then we will probably estimate the likelihood of our getting a speeding ticket as low.

Like the availability heuristic, the representativeness heuristic can lead to inaccurate judgments. Consider the following description:

Maria is a perceptive, sensitive, introspective woman. She is very articulate, but measures her words carefully. Once she’s certain she knows what she wants to say, she expresses herself easily and confidently. She has a strong preference for working alone.

On the basis of this description, is it more likely that Maria is a successful fiction writer or that Maria is a registered nurse? Most people guess that she is a successful fiction writer. Why? Because the description seems to mesh with what many people think of as the typical characteristics of a writer.

However, when you compare the number of registered nurses (which is very large) to the number of successful female fiction writers (which is very small), it’s actually much more likely that Maria is a nurse. Thus, the representativeness heuristic can produce faulty estimates if: (1) we fail to consider possible variations from the prototype or (2) we fail to consider the approximate number of prototypes that actually exist.

What determines which heuristic is more likely to be used? Research suggests that the availability heuristic is most likely to be used when people rely on information held in their long-term memory to determine the likelihood of events occurring. On the other hand, the representativeness heuristic is more likely to be used when people compare different variables to make predictions (Harvey, 2007).

The Critical Thinking box “The Persistence of Unwarranted Beliefs” on the next page discusses some of the other psychological factors that can influence the way in which we evaluate evidence, make decisions, and draw conclusions.

284