Appendix A: Powers-of-Ten Notation

Astronomy is a science of extremes. As we examine various cosmic environments, we find an astonishing range of conditions–from the incredibly hot, dense centers of stars to the frigid, near-perfect vacuum of interstellar space. To describe such divergent conditions accurately, we need a wide range of both large and small numbers. Astronomers avoid such confusing terms as “a million billion billion” (1,000,000,000,000,000,000,000,000) by using a standard shorthand system. All the cumbersome zeros that accompany such a large number are consolidated into one term consisting of 10 followed by an exponent, which is written as a superscript and called the power of ten. The exponent merely indicates how many zeros you would need to write out the long form of the number. Thus,

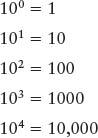
and so forth. Equivalently, the exponent tells you how many tens must be multiplied together to yield the desired number. For example, ten thousand can be written as 10⁴ (“ten to the fourth”) because 10⁴ = 10 × 10 × 10 × 10 = 10,000. Similarly, 273,000,000 can be written as 2.73 × 10⁸.

In scientific notation, numbers are written as a figure between 1 and 10 multiplied by the appropriate power of 10. The distance between Earth and the Sun, for example, can be written as 1.5 × 10⁸ km. Once you get used to it, you will find this notation more convenient than writing “150,000,000 kilometers” or “one hundred and fifty million kilometers.”

This powers-of-ten system can also be applied to numbers that are less than 1 by using a minus sign in front of the exponent. A negative exponent tells you that the location of the decimal point is as follows:

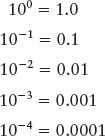
and so forth. For example, the diameter of a hydrogen atom is approximately 1.1 × 10⁻⁸ cm. That is more convenient than saying “0.000000011 centimeter” or “11 billionths of a centimeter.” Similarly, 0.000728 equals 7.28 × 10⁻⁴.

Using the powers-of-ten shorthand, one can write large or small numbers like these compactly:

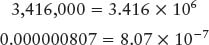
Because powers-of-ten notation bypasses all the cumbersome zeros, a wide range of circumstances can be numerically described conveniently:

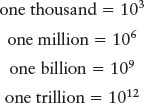
and also

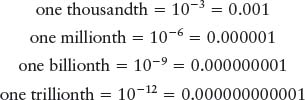
Try these questions: Write 3,141,000,000 and 0.0000000031831 in scientific notation. Write 2.718282 × 10¹⁰ and 3.67879 × 10⁻¹¹ in standard notation.

(Answers appear at the end of the book.)