The Relativity Theories

It seems reasonable that if I watch you traveling at, say, 100 km/h (about 60 mi/h), my measurements of your mass, the rate at which your watch runs, and the length of your car would be the same as the measurements you make of these things. In fact, the measurements will not be the same. At the beginning of the twentieth century, Einstein began a revolution in science by disregarding his common sense, making a few physical assumptions about nature, and using mathematics to explore their consequences. The resulting equations revealed profound, albeit highly counterintuitive, insights into how nature works. Armed with the equations that Einstein derived, scientists have been exploring and using the consequences of his theories to develop new technology and a deeper understanding of how matter, energy, space, and time interact.

14-1 Special relativity changes our conception of space and time

In 1905, Albert Einstein derived his theory of special relativity, a description of how motion affects our measurements of distance, time, and mass. He was guided by two assumptions. Although the implications of the theory proved revolutionary, the first notion seems simple:

In other words, as long as you are moving in a straight line at a constant speed, you experience the same laws of physics as anyone else moving at any other constant speed in a straight line and in any other direction. To illustrate this first idea, suppose you were inside a closed boxcar moving smoothly in a straight line at 100 km/h and you dropped a pen from a height of 2 m. You time how long it takes the pen to reach the floor (about 0.64 second). Then the train is stopped and you repeat the same experiment in the station. The time it would take the pen to fall would be identical.

The second idea seems more bizarre:

Suppose that you are in a (very powerful) car moving toward a distant street lamp at 150,000 km/s (93,000 mi/s). In simpler terms, this is 50% the speed of light, denoted 0.5c (Figure 14-1a). A friend of yours leaning on the lamppost sees you coming and also sees light from the lamp heading toward you at c. How fast do you see the photons of light coming at you? It would seem reasonable that you clock them at c + 0.5c, which is the speed of the photons toward you plus your speed toward them, but this is incorrect. You will, in fact, see the photons coming toward you with the same speed, c, that your friend sees them leaving the lamp (Figure 14-1b). You would, however, see that they have a different color than your friend sees. That difference is due to the Doppler shift, as explained in An Astronomer’s Toolbox 4-3.

Figure 14-1: The Speed of Light Is Constant (a) As seen from the ground, photons of light from the lamp are traveling toward the car with a speed v = c (ignoring the slight decrease in speed due to the presence of the air). (b) As seen from the car, moving toward the lamp at v = 0.5c, the photons are also traveling at the speed v = c. The difference in color between the light in the two figures is due to the Doppler shift.

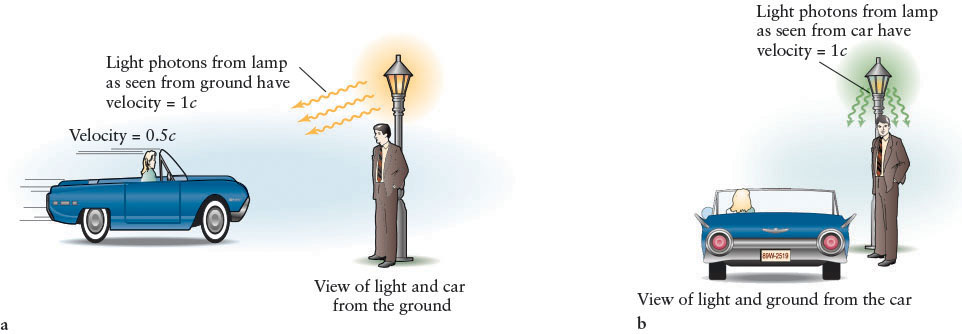
Einstein’s theory of special relativity expresses these two assumptions mathematically, and the results of these assumptions have been confirmed in innumerable experiments. Perhaps the most well-known result of special relativity is the relationship between matter and energy, E = mc². The fact that mass is multiplied by the square of a very large number reveals that a little mass creates a lot of energy. This equation implicitly states that, contrary to most daily experience (and what most people are taught as children), matter can be converted into energy and energy can be converted into matter. This conversion takes place when stars fuse elements together, like the hydrogen fusion that occurs in the Sun today.

Three other fundamental results of special relativity also defy our everyday experience:

1. The length of an object decreases as its speed increases. In other words, if a train moves toward or away from you, you would measure its length to be shorter than you would measure its length to be when it is stopped at the station (Figure 14-2). (This result also explains why the car in Figure 14-1 appears too short.) This result is called length contraction. However, if you measure the length of the moving train while you are moving with it, your measurement of its length will be the same as you measured on the ground when it was at rest. The word relativity emphasizes the importance of the relative speed between the observer and the measured object.
   
   

   Figure 14-2: Movement and Space According to the theory of special relativity, the faster an object moves, the shorter it becomes in its direction of motion as observed by someone not moving with the object. it becomes infinitesimally short as its speed approaches the speed of light. The dimensions perpendicular to the object’s motion are unchanged.
2. Clocks that you see as moving run more slowly than do clocks you see at rest. This result is called time dilation. Indeed, the faster a clock moves relative to you, the slower it appears to tick from your perspective. For example, air travelers actually age more slowly than they would if they did not fly (although because of the relatively low speeds of aircraft travel compared to the speed of light, this difference is imperceptibly small). People flying in aircraft do not feel time passing more slowly, however, because their biological activities slow down at the same rate as the clocks around them. Only an observer moving relative to an airplane sees that the clock and the activities of the high-speed travelers aboard the plane have slowed. These connections between motion and clocks mean that space and time cannot be considered as two separate concepts. Relativity requires us to combine them in a single entity, thus creating the concept of spacetime.
   

   Margin Question 14-1

   Question

   How much mass, m, would have to be destroyed to create an amount of energy, E?

3. The mass of an object increases as it moves faster. The concept of mass is discussed in Sections 2-5 and 2-7. The equations of special relativity reveal that an object moving at the speed of light would have an infinite amount of mass. It is impossible for any object with mass to reach this speed, much less go faster than the speed of light, because an infinite amount of mass is more than the total mass that exists in the universe. Furthermore, the equation F = ma (F is the force exerted on an object, m is its mass, and a is the acceleration it undergoes; see Section 2-7) reveals that if an object’s mass is infinite, the force necessary to accelerate this object must also be infinite. Because the total force available to move matter in the universe is finite, no massive object can be sped up to the speed of light: The speed of light is the universal speed limit.

14-2 General relativity explains how matter warps spacetime, creating gravitational attraction

While special relativity tells us how the mass of an object is related to its (constant) speed, this theory is special (in the sense of limited) because it does not account for the effects of acceleration and gravitation. These effects were incorporated by Einstein in 1915 into a more general theory, called the theory of general relativity (or, more simply, general relativity). It describes how spacetime changes shape in the presence of matter (Figure 14-3). The greater the mass, the more the distortion or curvature. Furthermore, the curvature of spacetime creates attraction between all pieces of matter in the universe (Figure 14-3c)—this attraction is what we call the gravitational force.

Figure 14-3: Curved Spacetime (a) This flat surface represents two dimensions in spacetime. in the absence of any matter in the spacetime, straight lines are straight in our intuitive sense (the sheet is flat). (b) in the presence of matter, spacetime curves, as shown by the curvature of the sheet when mass is laid on it. Straight lines, defined by the paths that light rays take, are no longer straight in the “usual” sense. Besides changing the path of photons, this curvature also creates gravity, which (c) pulls the two masses toward each other.

Another result of general relativity is that time slows down in the presence of matter. The greater the concentration of matter, the slower clocks tick (Figure 14-4). For example, time passes more slowly for us here on Earth’s surface than it would for astronauts on the Moon, which has less mass than Earth. Our technology has become so sophisticated that the slowing of time due to both relative speed, as discussed in Section 14-1, and slowing due to the presence of nearby matter, as shown in Figure 14-4, can be demonstrated in laboratories on Earth.

Figure 14-4: Time Slows Down Near Matter (a) Two clocks in space set at exactly the same time are (b) brought to earth and the Moon. from a vantage point far from earth and the Moon, the clock on earth is ticking more slowly than the clock on the Moon. This occurs because mass slows down the flow of time, and earth has more mass (and a higher density, which adds to the effect) than the Moon.

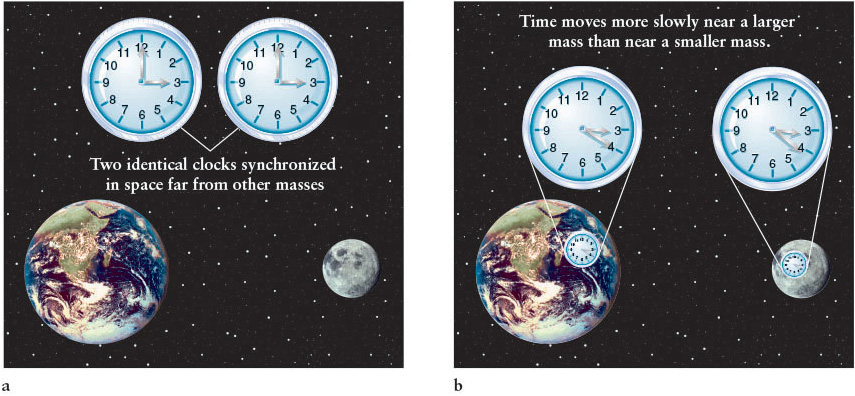
General relativity predicts more accurately the motion and other behaviors of matter than do Newton’s laws of motion and his law of gravitation. Newton’s laws are accurate only for objects with relatively small masses, slow velocities compared to the speed of light, and low densities (such as those for objects found on Earth). Newton’s laws are also limited to motion sufficiently far from large masses (such as the Sun) or high-density objects (such as neutron stars). We can use Newton’s laws to accurately predict the paths of projectiles on Earth and the motion of our planet around the Sun, but they do not describe the orbit of Mercury around the Sun very well (because that planet is so close to our star) or two neutron stars that orbit each other. In such cases, general relativity correctly predicts how objects move and how time passes. Closer to home, the accurate determination of location using GPS satellites orbiting Earth requires the use of the equations of general relativity.

14-3 Spacetime affects the behavior of light

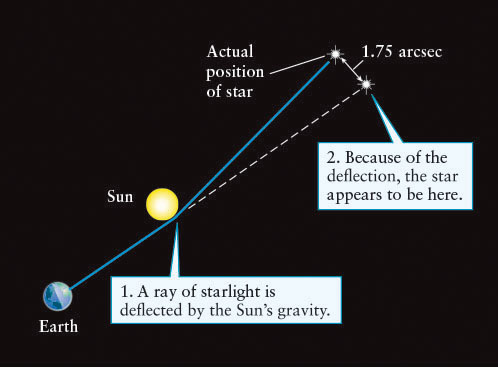
Besides affecting the behavior of objects, the curvature of spacetime changes the path and wavelength of light that passes near any matter. (These behaviors are not predicted by Newton’s laws.) Light travels along trajectories in space called geodesics. You can get an idea of how geodesics work by imagining that you are flying on the shortest possible route from one city to another. Your path would be analogous to a geodesic for a photon, and like that particle in the presence of matter in space, you would actually be following the curve of Earth’s surface, rather than going in a “straight line.” The first experimental verification of general relativity, made in 1919 during a solar eclipse, was its prediction that geodesics are sufficiently curved by the mass of the Sun to cause light from stars passing nearby to arc around it (Figure 14-5).

Figure 14-5: Curved Spacetime and the Path of Light The warping of space by matter causes light to be deflected. This was the first prediction of general relativity to be confirmed, in 1919. This confirmation came when stars behind the Sun were observed during an eclipse. The star in this drawing was not observed where it was supposed to be, as a result of the Sun’s gravity changing the path of its light.

Photons that leave the vicinity of a star also lose energy in climbing out of the star’s gravitational field. They do not slow down like a bullet fired upward. Rather, they shift to longer wavelengths (Figure 14-6), an effect we see in the spectra of some white dwarfs, whose light appears redder than it would if this effect did not occur. This shift of wavelengths leaving the vicinity of a massive object is called gravitational redshift.

Figure 14-6: Gravitational Redshift The color of light from the same object located at different distances from a mass appears different as seen from far away. The photons that leave the vicinity of the massive object lose energy and are therefore redshifted. The closer the light source is to the mass, the redder the light appears, and hence the name gravitational redshift. The same argument applies to light leaving the surfaces of different stars.

General relativity has been confirmed again and again, as seen in these observations:

• Light is measurably deflected by the gravitational curving of space due to the presence of matter like stars (see Figure 14-5) or entire galaxies containing billions of stars.
• The perihelion position of Mercury as seen from the Sun shifts, or precesses, by 43 arcsec per year more than is predicted by Newtonian gravitational theory (Figure 14-7). Its actual precession is exactly the amount predicted by general relativity.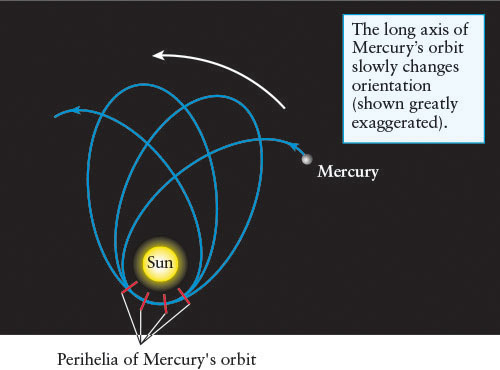
  
  

  Figure 14-7: Mercury’s Orbit Explained by General Relativity The location of Mercury’s perihelion (its position closest to the Sun) and its long axis of orbit change, or precess, with each orbit. This change occurs because of the gravitational influences of the other planets plus the curvature of space as predicted by einstein’s theory of general relativity. The amount of precession is inconsistent with the prediction of the orbit made by Newton’s law of gravity alone.
• The orbits of stars in binary systems follow the paths predicted by general relativity, rather than those predicted by Newtonian gravitation.
• The spectra of stars are observed to have the gravitational redshifts predicted by general relativity (see Figure 14-6).

14-4 General relativity predicts the fate of massive star cores—black holes

Let us now return to stellar evolution and consider what happens when high-mass main-sequence stars (with more than 25 M_⊙) explode as supernovae. As with the stars that contain between 8 M_⊙ and 25 M_⊙, high-mass stars become neutron stars. The neutron-star remnants of these high-mass stars, however, have more than 3 M_⊙. This is problematic because above this mass, the gravitational force of the neutron star overcomes the neutron degeneracy pressure created by the interactions among its particles. As a result, such remnant stars collapse further, and no force in nature can stop their infall.

We can use the equations of general relativity to understand the fate of collapsing neutron stars. We just saw that all matter warps the space around itself (see Figures 14-3 and 14-5). When matter gets sufficiently dense, it actually causes space near it to curve so much that it closes in on itself (Figure 14-8). Photons flying outward at an angle from such a collapsing star arc back inward. Photons flying straight upward redshift so much that they lose all their energy (see Section 3-3) and hence cease to exist.

Figure 14-8: Trapping of Light by a Black Hole (a) The paths and colors of light rays departing from a main-sequence, giant, or supergiant star are affected very little by the star’s gravitational force. (b) light leaving the vicinity of a white dwarf curves and redshifts more, whereas (c) near a neutron star, some of the photons actually return to the star’s surface. (d) inside a black hole, all light remains trapped. Most photons curve back in, except those that fly straight upward, which become infinitely redshifted, thereby disappearing.

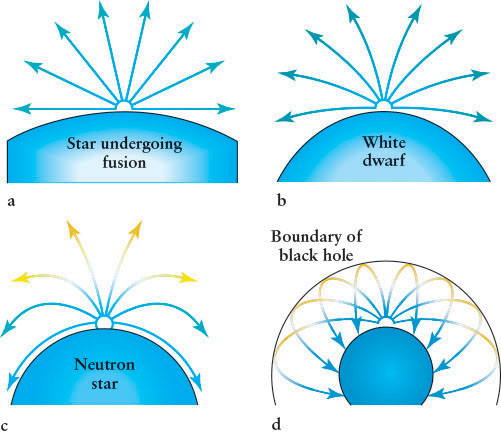
If light, the fastest moving of all known things, cannot escape from the vicinity of such dense matter, then nothing can! These regions out of which no matter or any form of electromagnetic radiation can leave are called black holes. Plummeting in on itself, a collapsing neutron star becomes so dense that it ceases to consist of neutrons. General relativity predicts that in creating a black hole, matter compresses to infinite density (and zero volume), a state called a singularity. However, we know that general relativity and our other theories of physics are invalid in such a situation. A more comprehensive theory of nature must be developed to explain the state of matter in a black hole’s singularity. Efforts are under way to develop such a theory. The best-known nascent explanation is called superstring theory, but it does not yet make testable predictions in this realm. All we can say with confidence is that the matter in black holes becomes incredibly dense and compact.