Inside a Black Hole
The formation of a black hole is complicated, but its nature is surprisingly simple: It contains matter at its center or in a ring, it has a boundary shaped like a sphere, it either has a net electric charge or does not, and it either rotates or it does not rotate.
441
14-5 Matter in a black hole becomes much simpler than elsewhere in the universe
 A black hole is separated from the rest of the universe by a boundary, called its event horizon. The event horizon is not like the surface of a solid or liquid body. No matter exists at this location except for the instant it takes infalling mass to cross the event horizon and enter the black hole.
A black hole is separated from the rest of the universe by a boundary, called its event horizon. The event horizon is not like the surface of a solid or liquid body. No matter exists at this location except for the instant it takes infalling mass to cross the event horizon and enter the black hole.
We cannot look inside a black hole because no electromagnetic radiation escapes from it. Our understanding of its structure comes from the equations of general relativity. According to Einstein’s theory, the event horizon is a sphere. The distance from the center of the black hole to its event horizon is called the Schwarzschild radius (abbreviated RSch), after the German physicist Karl Schwarzschild (1873–1916), who first determined its properties. An Astronomer’s Toolbox 14-1: The Sizes of Black Holes shows how to calculate this distance, which depends only on the black hole’s mass. The more massive the black hole, the larger its event horizon.
According to the equations of general relativity, when a stellar remnant collapses to a black hole, it loses its internal magnetic field. The field’s energy radiates away in the form of electromagnetic radiation and gravitational radiation. Emitted as gravitational waves, gravitational radiation travels as ripples in the very fabric of spacetime. Gravitational waves are also created when neutron stars or black holes collide or when stars and stellar remnants are in close orbits around each other. (Actually, gravitational radiation is emitted whenever any two things move around each other, such as a pair of dancers. When the moving bodies are less massive than stars or stellar remnants, however, we have no hope of detecting their very weak gravitational radiation with either present or projected technology.)
Gravitational radiation has not yet been directly detected, unlike, say, visible light that we “see” by its effects on our eyes or on a CCD. However, gravitational radiation has been observed indirectly by its effects on the orbits of some binary star systems. In particular, a pair of neutron stars orbiting each other emit so much energy as gravitational waves that the two bodies spiral toward each other. The change in their orbit is correctly predicted by general relativity. This agreement earned a Nobel Prize in Physics in 1993 for Joseph Taylor (1941–) and Russell Hulse (1950–), who discovered the first binary pulsar in 1974 and measured the changes in its neutron stars’ orbits.
The ripples in spacetime created by gravitational waves from stars or stellar remnants are incredibly tiny. On Earth, each meter-wide volume of space changes by less than 10−25 m as the waves pass by. Astronomers around the world are building gravitational wave detectors to measure these small changes (Figure 14-9). They have been in operation since 2002, but have yet to directly detect any gravity waves. Astronomers expect that the next generation of gravity wave detectors will provide a direct means to observe high-energy gravitational activity in the cosmos.

Characteristics of Black Holes
Besides losing its internal magnetic field, matter within a black hole loses almost all traces of its composition and origin. Indeed, it retains only three properties that it had before entering the black hole: its mass, its angular momentum, and its electric charge. Familiar concepts, such as proton, neutron, electron, atom, and molecule, no longer apply. In addition, because few large bodies appear to have a net charge, it is also doubtful that black holes do. We therefore predict that there are only two different types of black holes: those that rotate and those that do not.
AN ASTRONOMER’S TOOLBOX 14-1: The Sizes of Black Holes
In 1918, Karl Schwarzschild discovered the first solution of Einstein’s equations. His solution describes the nature of nonrotating black holes. According to Einstein’s theory of general relativity, the Schwarzschild radius RSch of any black hole can be found from its mass, M:
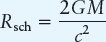
where RSch is measured in meters; M is the black hole’s mass in kilograms; c is the speed of light, 3 × 108 m/s2; and G is the gravitational constant, 6.67 × 10−11 m3/kg · s2. Expressing M in terms of solar masses, this equation can be conveniently approximated by
RSch ≈ 3 MBH
where MBH is the black hole’s mass in solar masses and RSch is in kilometers.
Example: A 5-M⊙ main-sequence star has a radius of 3 × 106 km, whereas the previous equation reveals that a black hole with the same mass has a 15-km Schwarzschild radius.
Try these questions: A primordial black hole with the mass of Mount Everest would have a Schwarzschild radius of just 1.5 × 10−15 m! What is Mount Everest’s mass? What is the Schwarzschild radius of a galactic black hole that contains 3 billion solar masses? A black hole with a Schwarzschild radius equal to the radius of Earth has how much mass?
(Answers appear at the end of the book.)
442
Types of Black Holes
If the mass creating a black hole is not rotating, the black hole that is formed does not rotate either. We call nonrotating black holes Schwarzschild black holes (Figure 14-10). General relativity predicts that all the mass in such a black hole collapses to a point of infinite density at its center, the singularity mentioned earlier. The rest of the volume from the event horizon to the singularity of a Schwarzschild black hole is empty space.
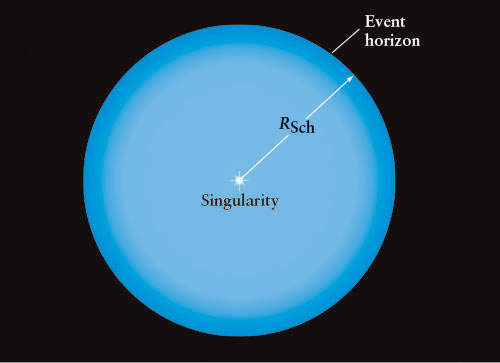
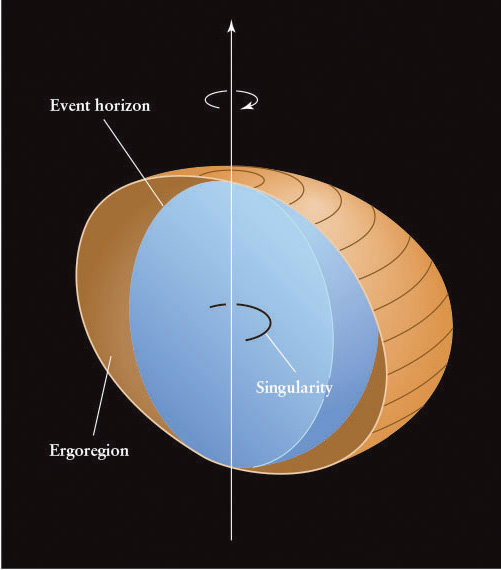
When the matter that creates a black hole possesses angular momentum, that matter collapses to a ring-shaped singularity located inside the black hole between its center and the event horizon (Figure 14-11). Such rotating black holes are called Kerr black holes, in honor of the New Zealand mathematician Roy Kerr (1934–), who first calculated their structure in 1963. Once again, the black hole is empty except for the singularity. Most Kerr black holes should be spinning thousands of times every second, even faster than the pulsars that we studied in Chapter 13. The black hole with the highest known rotation rate, discovered in 2006, rotates a thousand times per second, consistent with this theory.
Margin Question 14-5
Question
Where is the singularity of a rotating black hole?
443
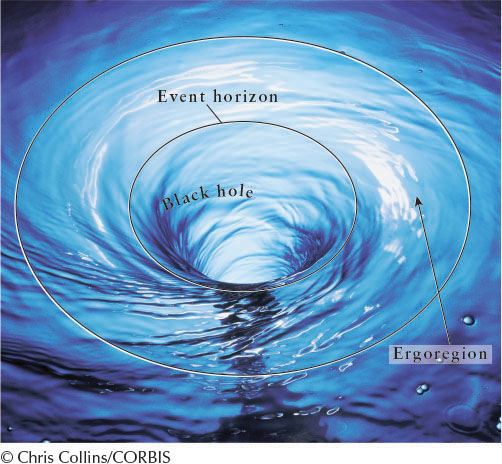
Kerr black holes cause nearby space to spiral around them like water in a drain (Figure 14-12). Whereas an object released from rest in the vicinity of a Schwarzschild black hole would fall straight into it, the same object released near a Kerr black hole will spiral inward (think of a cork being dragged around in the drain of Figure 14-12). This phenomenon is relevant in our study of quasars in Chapter 17. The equations of general relativity reveal that a swirling region of space called the ergoregion (see Figure 14-11) immediately outside the event horizon of each Kerr black hole forces all objects at rest in that region to fall into the black hole. If it is moving fast enough sideways, an object that enters the ergoregion can again fly out of it; however, if an object stops in the ergoregion, it must fall into the black hole. In 1997, matter orbiting a black hole was observed to behave in a fashion consistent with the existence of an ergoregion surrounding the hole. In the first decade of the twenty-first century, astronomers began observing spectra of atoms orbiting in the ergo regions of particularly massive black holes. The spectra showed the effects of gravitational redshift and Doppler shift predicted by Einstein’s general relativity for matter orbiting in these regions.
14-6 Falling into a black hole is an infinite voyage
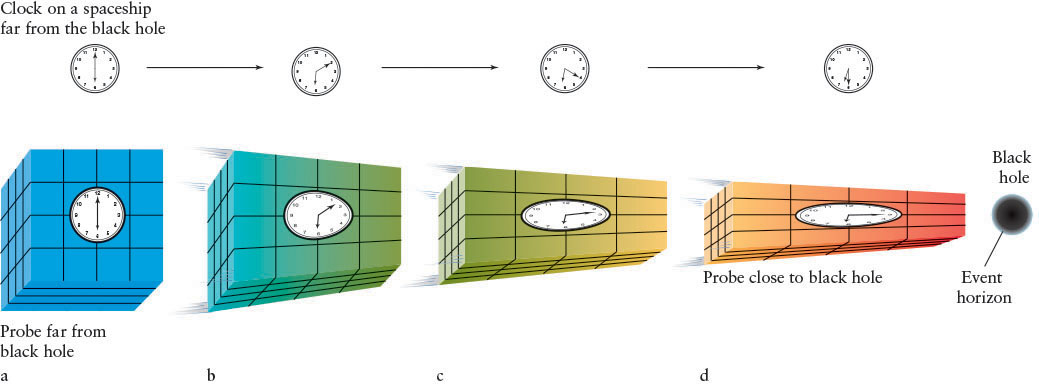
 Imagine being in a spacecraft orbiting only 1000 Schwarzschild radii (15,000 km) from an isolated 5-M⊙ black hole (see An Astronomer’s Toolbox 14-1 for the equation of the Schwarzschild radius). You are held in orbit by the black hole’s gravitational force. Even at that short distance, the only effect the black hole has on you is its gravitational attraction. Only when you get very, very close to the event horizon do bizarre things begin to happen. To investigate these changes, you send a cube-shaped probe with a clock toward the black hole, with the same side of the cube always facing “downward” toward the black hole. The probe emits a blue glow so that you can follow its progress. What happens to the cube as it approaches the black hole?
Imagine being in a spacecraft orbiting only 1000 Schwarzschild radii (15,000 km) from an isolated 5-M⊙ black hole (see An Astronomer’s Toolbox 14-1 for the equation of the Schwarzschild radius). You are held in orbit by the black hole’s gravitational force. Even at that short distance, the only effect the black hole has on you is its gravitational attraction. Only when you get very, very close to the event horizon do bizarre things begin to happen. To investigate these changes, you send a cube-shaped probe with a clock toward the black hole, with the same side of the cube always facing “downward” toward the black hole. The probe emits a blue glow so that you can follow its progress. What happens to the cube as it approaches the black hole?
 From the time you launch the probe until it reaches about 100 Schwarzschild radii (1500 km), you see the probe descend as if it were falling toward a planet or moon (Figure 14-13a). The passage of time indicated by the probe’s clock during this early stage of its infall slows down only slightly compared to your clock time farther away from the hole. At 100 Schwarzschild radii, however, the probe begins to respond significantly to the powerful tidal effect from the black hole. The face of the probe closest to the event horizon receives perceptibly more gravitational pull from the hole than its farther-away parts, and it begins to stretch apart.
From the time you launch the probe until it reaches about 100 Schwarzschild radii (1500 km), you see the probe descend as if it were falling toward a planet or moon (Figure 14-13a). The passage of time indicated by the probe’s clock during this early stage of its infall slows down only slightly compared to your clock time farther away from the hole. At 100 Schwarzschild radii, however, the probe begins to respond significantly to the powerful tidal effect from the black hole. The face of the probe closest to the event horizon receives perceptibly more gravitational pull from the hole than its farther-away parts, and it begins to stretch apart.
Margin Question 14-6
Question
How would a 1-M⊙ black hole 1 AU from earth affect our planet?
444
By the time that the probe comes within a few Schwarzschild radii of the event horizon, the tidal forces on it are so great that it violently elongates. The part of the probe closest to the black hole accelerates downward and away from the rest of the probe. Furthermore, the sides of the probe are drawn together: They are falling in straight lines toward a common center. The net gravitational effect of moving close to the event horizon is for the probe to be pulled long and thin (see Figure 14-13). From a practical perspective, this means that the probe would be violently torn apart, because it is not composed of perfectly elastic material.
As the probe nears the black hole, the blue photons leaving it must give up more and more energy to escape the increasing gravitational force. However, unlike a projectile fired upward, photons cannot slow down. Rather, they lose energy by increasing their wavelengths (see An Astronomer’s Toolbox 3-1: Photon Energies, Wavelengths, and Frequencies). This is another example of the gravitational redshift predicted by general relativity. The closer the probe gets to the event horizon, the more its light is redshifted—first to green, then yellow, then orange, then red, then infrared, and, finally, radio waves (see Figure 14-13b, c, d).
Stranger still is the black hole’s effect on time. General relativity predicts that when the probe approaches within a few Schwarzschild radii of the black hole, its infall rate will slow down as seen from far away. Also, signals from the probe show you that its clocks are running much more slowly than they did when it left your spacecraft. Time dilation becomes so great near the event horizon that the probe will appear to hover above it and its clocks will stop.
Anyone in the probe would observe something else altogether: They see the probe actually cross the event horizon and continue falling toward the black hole’s singularity in a normal period of time, according to their own watch. Pulled apart by tidal effects, the probe disintegrates as it falls inward. Contrary to the science fiction concept of traveling great distances quickly by passing through a black hole, calculations indicate that objects entering them could not survive passage through, even if there were a way to come out somewhere else.
 Could a black hole be connected to another part of spacetime or even some other universe? General relativity predicts such connections, called wormholes, for Kerr black holes, but astrophysicists are skeptical that the equations are correct in this regard. Their conviction is called cosmic censorship: Nothing can leave a local region of space that contains a singularity (that is, a black hole).
Could a black hole be connected to another part of spacetime or even some other universe? General relativity predicts such connections, called wormholes, for Kerr black holes, but astrophysicists are skeptical that the equations are correct in this regard. Their conviction is called cosmic censorship: Nothing can leave a local region of space that contains a singularity (that is, a black hole).