The Big Bang

The universe consists of all matter, energy, and spacetime that we can ever detect or that will ever be able to affect us. (We use this definition because there may be matter and energy in other dimensions or matter and energy that are moving away from us so quickly that their influence will never reach us.) So far in this text, we have explored matter on size scales from atoms to superclusters of galaxies. We also learned in Section 16-12 that the superclusters are all moving away from one another, implying that the universe is expanding. In this chapter we take the observational evidence from the rest of the book and use it to explore the Big Bang theory of cosmology. Cosmology is the study of the large-scale structure and evolution of the universe.

18-1 General relativity predicts an expanding (or contracting) universe

Modern cosmology almost began in 1915, when Einstein published his theory of general relativity. To his surprise and dismay, the relativity equations predicted that the universe is not static: They indicated that it should be either expanding (which it is) or contracting. But Einstein was not ready for what the equations were telling him.

At the time that Einstein published the theory of general relativity, the existence of galaxies and clusters and superclusters of galaxies had not yet been established and the 1925 discovery of the Hubble flow (Section 16-12) was a decade away. The prediction of a changing universe flew in the face of the then widely accepted belief in an infinite, static universe, a concept promoted by Isaac Newton more than two centuries earlier. Newton believed that each star is fixed in place and held under the influence of a uniform gravitational pull from every part of the cosmos. If the stars were not uniformly distributed, he argued, one region would have more mass than another. The denser region’s gravity would then attract other stars, causing them to further clump together. Because he did not observe this clumping, Newton concluded that the stars in the universe must be distributed uniformly over an infinite space.

The apparently static universe and the prevailing philosophy that the universe had existed forever made Einstein doubt the implications of his own theory, so he missed the opportunity to propose that we live in a changing universe. Instead, he adjusted his elegant equations to yield a static, finite cosmos. He did this by adding a repulsive (outward-pushing) term, called the cosmological constant, to his equations so that gravity’s normal attractive force would be counterbalanced and the universe would be static. After observations revealed that the universe is expanding, Einstein said that adding the cosmological constant was the biggest blunder of his career.

Although the value of the cosmological constant that Einstein inserted was wrong, the concept of such a constant may be correct. Observations since 1997 indicate that the universe is not just expanding but actually accelerating outward. This acceleration means that there must be an outward pressure that more than counter-acts the effects of normal gravitation, which is trying to slow the universe’s expansion. One of the two current theories that can explain this acceleration is the presence of a cosmological constant that creates the outward pressure. We discuss these two theories further in Section 18-15.

18-2 The expansion of the universe creates a Dopplerlike redshift

Edwin Hubble is credited with discovering that we live in an expanding universe (see Section 16-12). The redshifts of clusters and superclusters of galaxies that Hubble found moving away from us appear to be produced by the Doppler effect, but they actually are not. Recall that the normal Doppler shift is caused by an object moving toward or away from us through fixed spacetime (see Section 4-7). However, using Einstein’s theory of general relativity, we find that spacetime, the fabric of the universe, is not fixed but is actually expanding. This expansion is what is carrying the superclusters away from each other and, in many cases, carrying clusters in a given supercluster away from one another. (The gravitational force that holds objects like planets and stars and entire galaxies together is so strong that these bodies and systems are not being pulled apart. The expansion of space just acts to increase the separation between superclusters of galaxies and between clusters of galaxies in the same supercluster that are not gravitationally bound to each other.)

The redshift that Hubble observed, caused by the expansion of the universe, is properly called the cosmological redshift. In other words, the photons that we observe from galaxies in other superclusters are all redshifted because space is expanding. To understand why, consider a wave drawn on a rubber band (Figure 18-1). The wave has an unstretched wavelength (see Section 3-1) of λ₀. As the rubber band stretches, the wavelength increases (λ > λ₀). Now imagine a photon coming toward us from a distant galaxy. As the photon travels through space, space is expanding, and, like stretching the rubber band, this expansion stretches the photon’s wavelength. When the photon reaches our eyes, we see a drawn-out wavelength—the photon is redshifted. The longer the photon’s journey, the more its wavelength is stretched by the expansion of the universe. Therefore, astronomers observe larger redshifts in photons from relatively distant galaxies than in photons from relatively nearby galaxies.

Figure 18-1: Cosmological Redshift Just as the waves drawn on this rubber band are stretched along with the rubber band, so too are the wavelengths of photons stretched as the universe expands.

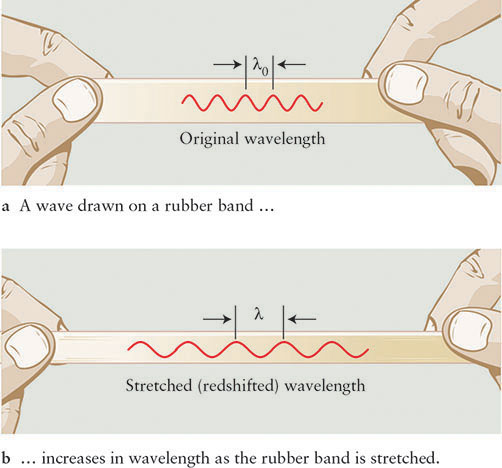
As we saw in Section 16-12, Hubble discovered the linear relationship between the distances to galaxies in other superclusters and the redshifts of those galaxies’ spectral lines. For example, a galaxy twice as far from Earth as another galaxy has twice the cosmological redshift of the closer one. The normal Doppler shift has the same relationship. As a result of the two effects being described by the same equations, the normal Doppler shift and the cosmological redshift predict the same relationship between redshift and motion—except for the most distant galaxies and quasars, where effects of relativity must be taken into account. Working with relatively nearby galaxies, Hubble was fully justified in using the “normal” Doppler equation to calculate the recession of galaxies.

18-3 The Hubble constant is related to the age of the universe

Hubble’s law gives us a way to estimate the age of the universe. Imagine watching a movie of two superclusters receding from each other. If we then run the film backward, time runs in reverse, and we observe all the superclusters coming together. The time it would take for them all to collide is the time since they were last combined as a single clump of matter. Assuming that the universe began expanding when it came into existence and that it has always expanded at a constant rate, we can use a simple equation to estimate the age of the universe:

Recall that Hubble found the relationship

which we can rewrite as

Comparing the first and last equations here (see An Astronomer’s Toolbox 18-1: H₀ and the Age of the Universe), we see that Hubble’s constant is the reciprocal of the time since the universe began. Using a Hubble constant of 71.1 km/s/Mpc, we find:

As of 2013, the most accurate measurement is 13.77 ±0.059 billion years. In what follows, we will simply use an age of 13.8 billion years.

18-4 Remnants of the Big Bang have been detected

In 1927, the Belgian astrophysicist and Catholic priest Georges Lemaître (1894–1966) proposed that, as a consequence of the equations of Einstein’s theory of general relativity, the universe is expanding. Using Hubble’s subsequent observations of an expanding universe, Lemaître logically concluded that the superclusters must have expanded from a much smaller volume. He proposed that the universe began as an extraordinarily hot and dense primordial atom of energy. Just as energy created in an explosion causes debris to expand outward, the primordial energy created at the beginning of time caused the universe to expand. This initial event is now called the Big Bang. Space and time (that is, spacetime; see Chapter 14) did not exist before that moment. Rather than expanding into preexisting spacetime, the Big Bang explosion created spacetime, and that spacetime (in which we live) has been expanding ever since. The Big Bang led to the formation of all spacetime, matter, and energy. As noted earlier in this chapter, science does not yet have an explanation for why the Big Bang occurred.

Shortly after World War II, the astrophysicists Ralph Alpher (1921–2007) and George Gamow (1904–1968) proposed that a fraction of a second after the Big Bang, the universe was an incredibly hot blackbody—in excess of 10³² K. As heat is a measure of how many photons there are and how energetic they are, the early universe must therefore have been filled with intensely high-energy electromagnetic radiation. As the universe expanded, the cosmological redshift stretched these gamma rays to longer and longer wavelengths so that most of the photons left over from this event are now radio waves. Recall from Section 3-3 that photon energies decrease with increasing wavelength. Because the early photons are being redshifted, the energy they each have is decreasing. This energy is measured as heat, so the universe is cooling off as it expands.

Calculations indicated that if the universe began with a hot Big Bang, the remnants of that energy should still fill all space today, giving the entire universe a temperature only a few kelvins above absolute zero. This radiation is called the cosmic microwave background because the peak of its blackbody spectrum should lie in the microwave part of the radio spectrum. In the early 1960s, Robert Dicke (1916–1997), P. J. E. Peebles (1935–), David Wilkinson (1935–2002), and their colleagues at Princeton University began designing a microwave radio telescope to detect it.

Meanwhile, just a few miles from Princeton, two physicists had already detected the cosmic background radiation. Arno Penzias (1933–) and Robert Wilson (1936–) of Bell Laboratories were working on a new horn antenna designed to relay telephone calls to Earth-orbiting communications satellites (Figure 18-2). However, Penzias and Wilson were mystified. No matter where in the sky they pointed their antenna, they detected a faint background noise. All efforts to eliminate this background noise failed, even the careful removal of static noise-generating pigeon droppings from the antenna.

Figure 18-2: RIVUXG Bell Labs Horn Antenna This Bell Laboratories horn antenna at Holmdel, New Jersey, was used by Arno Penzias (right) and Robert Wilson in 1965 to detect the cosmic microwave background.

Thanks to a colleague, they learned of the then theoretical cosmic microwave background and the work of Dicke, Peebles, and Wilkinson in trying to locate it. Communicating with the Princeton astronomers, Penzias and Wilson presented their finding and thus were able to claim the first detection—their annoying noise was, in fact, the remnant energy of the Big Bang. The cosmic microwave background is required by the Big Bang theory but is neither required nor predicted by any other competing cosmological theory. Detection of the cosmic microwave background is the principal reason why the Big Bang is accepted by astronomers as the correct cosmological theory.

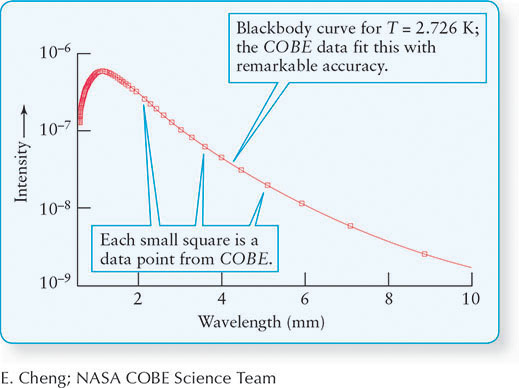
Precise measurements of the cosmic microwave background were first made by the Cosmic Background Explorer (COBE) satellite, which operated between 1989 and 1994. The radiation has since been measured more precisely by other equipment, such as the Wilkinson Microwave Anisotropy Probe (WMAP) and the balloon-carried BOOMERANG (Figure 18-3). The data taken by COBE and shown in Figure 18-4 reveal that, as predicted, this ancient radiation has the spectrum of a blackbody with a temperature of approximately 2.73 K (referred to as the 3-degree background radiation). The observations by COBE earned the 2006 Nobel Prize in Physics for astrophysicists John C. Mather (1946–) and George F. Smoot (1945–).

Figure 18-3: RIVUXG In Search of Primordial Photons (a) The Wilkinson Microwave Anisotropy Probe (WMAP) satellite, launched in 2001, improved upon the measurements of the spectrum and angular distribution of the cosmic microwave background taken by the COBE satellite. (b) The balloon-carried telescope BOOMERANG orbited above Antarctica for 10 days, collecting data used to resolve the cosmic microwave background, with 10 times higher resolution than that of COBE. All of these experiments found local temperature variations across the sky but no overall deviation from a blackbody spectrum.

Figure 18-4: Spectrum of the Cosmic Microwave Background The little squares on this graph are COBE’s measurements of the brightness of the cosmic microwave background plotted against wavelength. To a remarkably high degree of accuracy, the data fall along a blackbody curve for 2.73 K. The peak of the curve is at a wavelength of 1.1 mm, in accordance with Wien’s law.

The photons of the 3-degree background radiation are not the only remnants of the Big Bang that astronomers have found. In 2008, neutrinos created along with the photons in the Big Bang were indirectly observed by WMAP. (Recall from Section 10-9 that neutrinos are also created today in the nuclear fusion occurring in the Sun and other stars.) The discovery of these cosmic neutrinos was made by comparing the predicted effects of those neutrinos on the young universe with observations of the earliest observable remnants of the Big Bang, about which we will have more to say shortly. The theory of these neutrinos and the observations of their predicted effects agree to high precision. The numbers of neutrinos in the cosmic neutrino background is impressive: Several million of them pass through your body every second. There are similar numbers of neutrinos in similar volumes of space everywhere in the universe.

18-5 The universe has two symmetries—isotropy and homogeneity

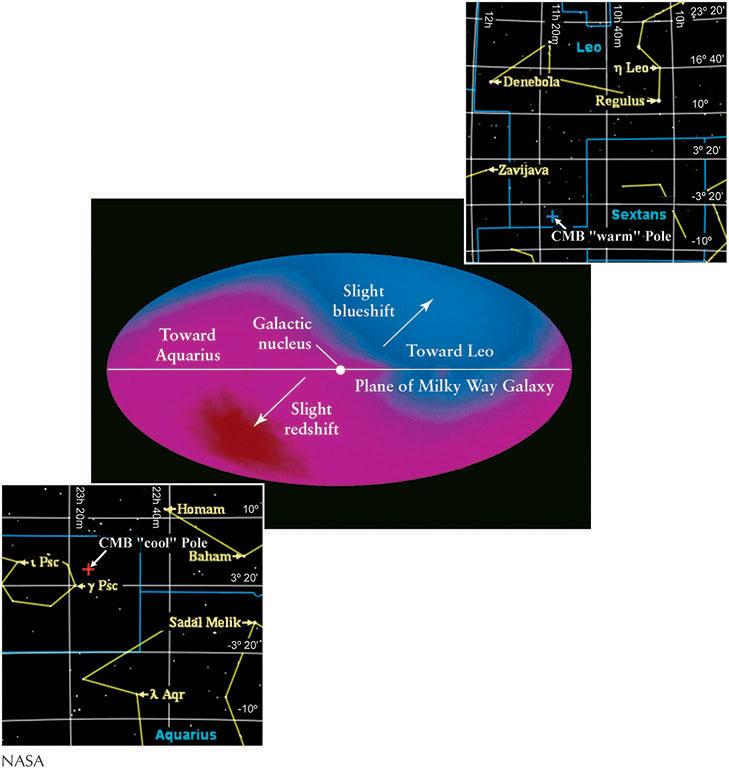
Observations show that the cosmic microwave background is almost perfectly isotropic: Its intensity is nearly the same in every direction in the sky. Indeed, if you could look at the cosmic microwave background from all directions in the entire universe with the naked eye, it would appear as uniform as a well-painted wall. However, when extremely high resolution measurements are made, tiny differences in the temperature of the universe are observed in different directions. One difference is caused by our motion through the cosmic microwave background. Figure 18-5 shows a map of the microwave sky. It is very, very slightly warmer than average in the direction of the constellation Leo and slightly cooler in the opposite direction, toward Aquarius. The observed temperature differences shown in Figure 18-5 mean that the solar system is moving toward Leo at a speed of 390 km/s. These observations can be understood as follows: As we move toward Leo, our motion through the cosmic microwave background radiation creates a normal Doppler shift that causes photons from that direction to appear to have shorter wavelengths—radiation from the direction of Leo is blueshifted, whereas radiation from the opposite direction, Aquarius, is redshifted because we are moving away from that region (Figure 18-6). Furthermore, a photon’s wavelength determines its energy (see Section 3-3). The energy of the photons then determines the temperature that we measure for that part of the sky. Observing slightly shorter-wavelength photons in the direction of Leo means that space in that direction appears slightly warmer, because of our motion, than does space in other directions.

Figure 18-5: RIVUXG Microwave Sky This map of the microwave sky was produced from data taken by instruments on board COBE. The galactic center is in the middle of the map, and the plane of the Milky Way runs horizontally across the map. Color indicates Doppler shift and temperature: Blue is where the microwave background is blueshifted and appears warmer, while red is where it is redshifted and appears cooler. This Doppler shift across the sky is caused by Earth’s motion through the microwave background. The resulting variation in background temperature is quite small, only 0.0033 K above the average radiation temperature of 2.726 K (which we have rounded to 2.73 K in the text).

Figure 18-6: Our Motion Through the Microwave Background Because of the Doppler effect, we detect shorter wavelengths in the microwave background and a higher temperature of radiation in that part of the sky toward which we are moving. This part of the sky is the area shown in blue in Figure 18-5. In the opposite part of the sky, shown in red in Figure 18-5, the microwave radiation has longer wavelengths and a cooler temperature.

Taking into account the known velocity of the Sun around the center of our Galaxy, astronomers calculate that the entire Milky Way Galaxy is moving relative to the cosmic microwave background at 600 km/s—some 1.3 million mi/h—in the general direction of the Centaurus cluster. The gravitational attraction of four nearby clusters of galaxies, most significantly the Great Attractor, and an enormous supercluster called the Shapley concentration, is believed to be pulling us in that direction. Subtracting the motions of Earth, the Sun, the Milky Way, and the Local Cluster (of galaxies) with respect to the microwave background, the average intensity of radiation is found to be the same in all directions (that is, isotropic) to about 1 part in 100,000.

Although the existence of the cosmic background radiation provides compelling support for the Big Bang theory, its near-isotropy was, until recently, a major problem. The issue was that the original Big Bang theory did not require space to be isotropic—after accounting for Earth’s motion through the cosmos, the temperature in one direction could have been many degrees different than the temperature in any other direction, but it is not.

Isotropy is not limited to the blackbody radiation observed throughout the universe. It is also found on sufficiently large scales when exploring the numbers of galaxies in different directions. Astronomers have counted the numbers of galaxies at different distances from us and in a variety of directions. The number of galaxies stays roughly constant with respect to both distance and direction, allowing, as we saw in Section 16-8, for the distribution of most galaxies on the boundaries of sponge-shaped regions or bubbles throughout the universe. Because of this uniformity with distance, we say that the universe is also homogeneous. Isotropy and homogeneity must be explained by any viable theory of cosmology, such as the Big Bang.

The need to explain isotropy and homogeneity, among other things, has led to numerous refinements in the Big Bang theory. As a result, this theory now provides an accurate scenario for the evolution of the universe from a tiny fraction of a second after it formed and onward.