Patterns of Stars

When you gaze at the sky on a clear night where the air is free of pollution and there is not too much light from cities or other sources, there seem to be millions of stars twinkling overhead. In reality, the unaided human eye can detect only about 6000 stars over the entire sky. At any one time, you can see roughly 3000 stars in dark skies, because only half of the stars are above the horizon—the boundary between Earth and the sky. In very smoggy or light-polluted cities, you may see only a tenth of that number or less (see Figure 1-1).

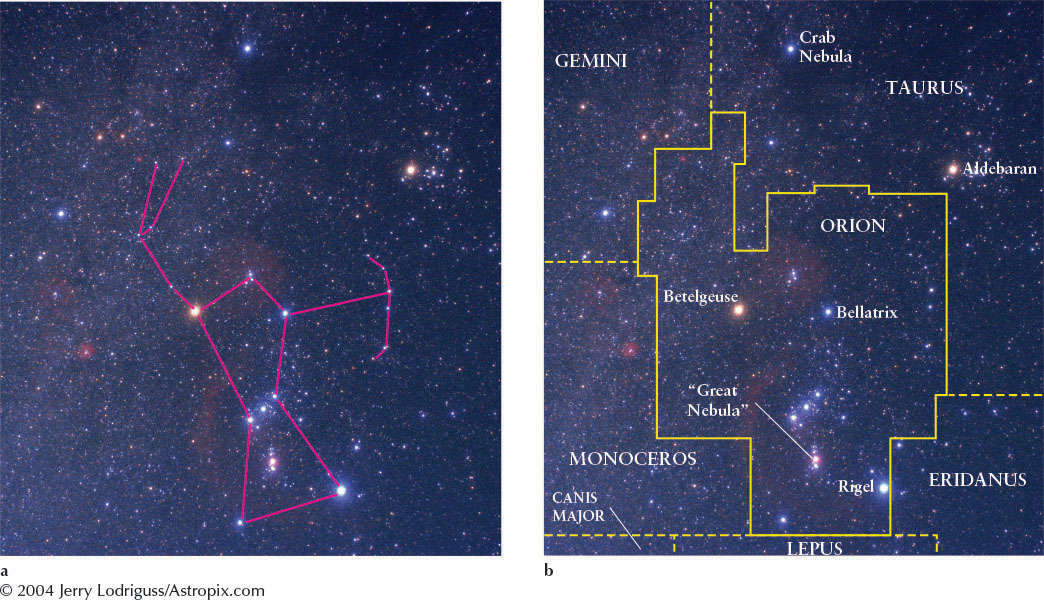
In any event, you probably have noticed patterns of bright stars, each technically called an asterism, and you are familiar with some common names for some of them, such as the ladle-shaped Big Dipper and broad-shouldered Orion. These recognizable patterns of stars (Figure 1-4a) are informally called constellations in everyday conversation. Technically, however, constellations are entire regions of the sky and everything in them. In what follows, we will often use the word “constellation” to mean either the asterisms or the regions of the sky. Be careful to consider which version of the word is in use.

Figure 1-4: The Constellation Orion (a) The pattern of stars (asterism) called Orion is prominent in the winter sky. From the northern hemisphere, it is easily seen high above the southern horizon from December through March. You can see in this photograph that the various stars have different colors—something to watch for when you observe the night sky. (b) Technically, constellations are entire regions of the sky. The constellation called Orion and parts of other nearby constellations are depicted in this photograph. All the stars and other celestial objects, like galaxies, inside the boundary of Orion are members of that constellation. The entire sky is covered by a quilt-like pattern of 88 constellations of differing sizes and shapes.

1-2 Well-known constellations make locating more obscure stars and constellations easy

People have known for millennia how to find the direction north in locations where the Big Dipper is visible. To do this, locate the Big Dipper (the asterism in the constellation Ursa Major) and imagine that its bowl is resting on a table (Figure 1-5). If you see the dipper upside down in the sky, as you frequently will, imagine the dipper resting on an upside-down table above it. Locate the two stars of the bowl farthest from the Big Dipper’s handle. These are called the pointer stars. Draw a mental line through these stars in the direction away from the table, as shown in Figure 1-5. The first moderately bright star you then encounter is Polaris, also called the North Star because it is located almost directly over Earth’s North Pole. So, while Polaris is not even among the 20 brightest stars (see Appendix E-6), it is easy to locate. Whenever you face Polaris, you are facing north. East is then on your right, south is behind you, and west is on your left. (There is no equivalent star over the South Pole.)

Figure 1-5: The Big Dipper as a Guide In the northern hemisphere, the Big Dipper is an easily recognized pattern of seven bright stars. This star chart shows how the Big Dipper can be used to locate Polaris (the North Star) as well as the brightest stars in three other constellations. While the Big Dipper appears right side up in this drawing of the sky shortly before sunrise, at other times of the night it appears upside down.

The Big Dipper also illustrates the fact that being familiar with just a few constellations makes it easy to locate less distinctive stars and other constellations. The most effective way to do this is to use vivid visual connections, especially those of your own devising. For example, imagine gripping the handle of the Big Dipper and slamming its bowl straight down onto the head of Leo (the Lion). Leo comprises the first group of bright stars your dipper encounters. As shown in Figure 1-5, the brightest star in this group is Regulus, the dot of the backward question mark that traces the lion’s mane. As another example, follow the arc of the Big Dipper’s handle away from its bowl. The first bright star you encounter along that arc beyond the handle is Arcturus in Boötes (the Herdsman). Follow the same arc farther to the prominent bluish star Spica in Virgo (the Virgin). Spotting these stars and remembering their names are easy if you remember the saying “Arc to Arcturus and speed on to Spica.”

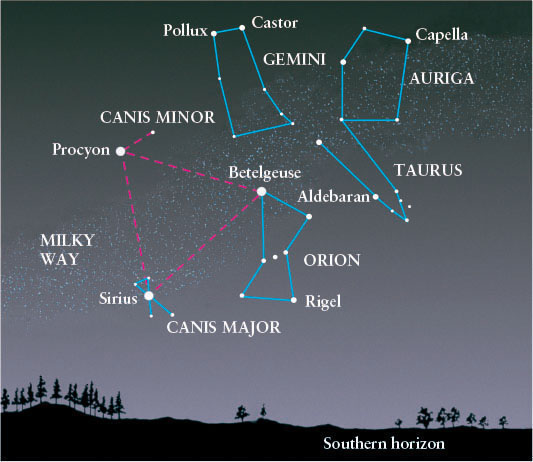
Different constellations are visible at night during different times of the year. During the winter months in the northern hemisphere, you can see some of the brightest stars in the sky. Many of them are in the vicinity of the “winter triangle,” which connects bright stars in the constellations of Orion (the Hunter), Canis Major (the Larger Dog), and Canis Minor (the Smaller Dog), as shown in Figure 1-6. The winter triangle passes high in the sky at night during the middle of winter. It is easy to find Sirius, the brightest star in the night sky, by locating the belt of Orion and following a straight mental line from it to the left (as you face Orion). The first bright star that you encounter is Sirius.

Figure 1-6: The Winter Triangle This star chart shows the southern sky as it appears during the evening in December. Three of the brightest stars in the sky make up the winter triangle. In addition to the constellations involved in the triangle, Gemini (the Twins), Auriga (the Charioteer), and Taurus (the Bull) are also shown.

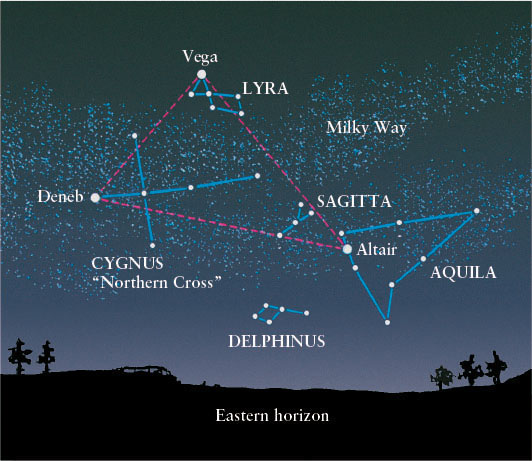
The “summer triangle,” which graces the summer sky as shown in Figure 1-7, connects the bright stars Vega in Lyra (the Lyre), Deneb in Cygnus (the Swan), and Altair in Aquila (the Eagle). A conspicuous portion of the Milky Way forms a beautiful background for these constellations, which are nearly overhead during the middle of summer at midnight. For more on the constellations, see Guided Discovery: The Stars and Constellations.

Figure 1-7: The Summer Triangle This star chart shows the northeastern sky as it appears in the evening in June. In addition to the three constellations involved in the summer triangle, the faint stars in the constellations Sagitta (the Arrow) and Delphinus (the Dolphin) are also shown.

Astronomers require more accuracy in locating dim objects than is possible simply by moving from asterism to asterism. They have therefore created a sky map, called the celestial sphere, and applied a coordinate system to it, analogous to the coordinate system of north-south latitude and east-west longitude used to navigate on Earth. If you know a star’s celestial coordinates and know how to navigate around the night sky, you can locate it quickly. For such a sky map to be useful in finding stars, the stars must be fixed on it, just as cities are fixed on maps of Earth.

1-3 The celestial sphere aids in navigating the sky

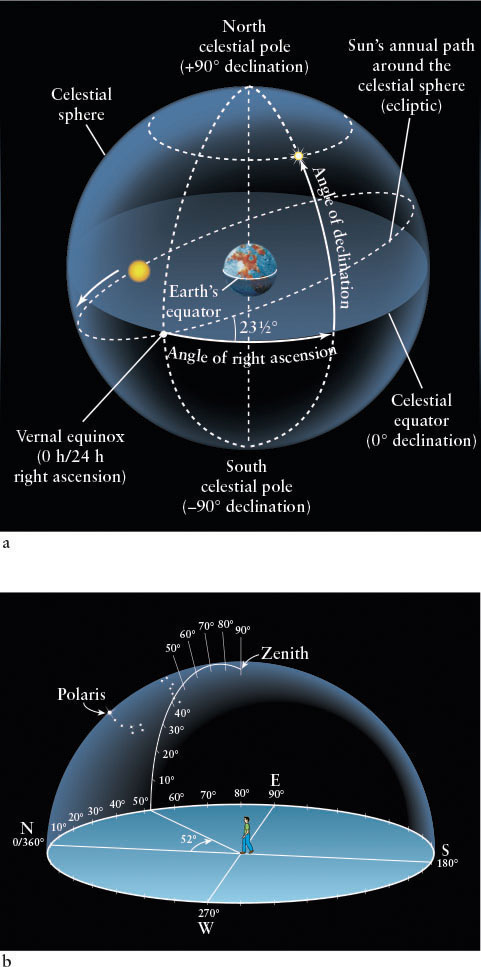
If you look at the night sky year after year, you will see that the stars do indeed appear fixed relative to one another. Furthermore, throughout each night the entire pattern of stars appears to rigidly orbit Earth. We employ this artificial, Earth-based view of the heavens to make celestial maps by pretending that the stars are attached to the inside of an enormous hollow shell, the celestial sphere, with Earth at its center (Figure 1-8). Visualized another way, you can imagine the half of the celestial sphere that is visible at night as a giant dome covering Earth.

Figure 1-8: The Celestial Sphere and Coordinate Systems (a) The celestial sphere is the apparent “bowl” or hollow sphere of the sky. The celestial equator and poles are projections of Earth’s equator and axis of rotation onto the celestial sphere. The north celestial pole is therefore located directly over Earth’s North Pole, while the south celestial pole is directly above Earth’s South Pole. Analogous to longitude and latitude on Earth, lines of constant right ascension (R.A.) run along the celestial sphere between the poles, while lines of constant declination (Dec.) circle the celestial sphere parallel to the celestial equator. The star in this figure has the indicated R.A. and Dec. (b) Altitude and azimuth create a local coordinate system for every place on Earth. Altitude is the angle straight up from the horizon. Azimuth is the angle eastward from north along the horizon. To find Mizar at 10 p.m. on March 14, 2013, as seen from Orono, Maine, we calculate its coordinates there as altitude 47° and azimuth 52° and use them to locate it in the night sky.

Students being shown a celestial sphere.

Whereas asterisms such as the Big Dipper are often called “constellations” in normal conversation, astronomers formally use the word constellation to describe an entire area of the celestial sphere and all the objects in it, as mentioned above (see Figure 1-4b). (Keep in mind that most constellations and their asterisms—the recognizable star patterns—have the same name. For example, Orion is the name of a constellation, as well as the associated asterism, which sometimes complicates conversation.) The celestial sphere is divided into 88 constellations of differing sizes and shapes.

The boundaries of the constellations are all straight lines that meet at right angles (see Figure 1-4b). Some constellations, like Ursa Major (the Large Bear), are very large, while others, like Sagitta (the Arrow), are relatively small. To describe a star’s location, we might say “Albireo in the constellation Cygnus (the Swan),” much as we would refer to “Chicago in the state of Illinois,” “Melbourne in the state of Victoria,” or “Ottawa in the province of Ontario.”

Stars are actually at a wide variety of distances from Earth, and they are moving relative to each other. But we neither see their motion nor perceive their relative distances because they are so far from us. You can understand this difficulty in seeing distant objects moving by first imagining a car driving right past you at 100 km/h (62 mph). Its motion is unmistakable. However, a plane traveling at 1000 km/h across the sky appears to be moving much more slowly. And an object at the distance of the Sun traveling at the same speed as the plane across the sky would appear to be going nearly 100 million times more slowly than that plane.

The stars (other than the Sun) are all more than 40 × 10¹² km (40 trillion km or 25 trillion mi) from us. Therefore, although the patterns of stars in the sky do change, their great distances prevent us from seeing those changes over the course of a human lifetime. Thus, as unrealistic as it is to assume that all the stars are fixed in space and that all are at the same distance from us, the celestial sphere is so useful for navigating the heavens that it is used by astronomers even at the most sophisticated observatories around the world.

As shown in Figure 1-8a, we can project key geographic features from Earth out into space to establish directions and bearings. If we expand Earth’s equator onto the celestial sphere, we obtain the celestial equator, which divides the sky into northern and southern hemispheres, just as Earth’s equator divides Earth into two hemispheres. We can also imagine projecting a straight line between Earth’s North Pole and South Pole out into space above both poles. Where this line intersects the celestial sphere defines the north celestial pole and the south celestial pole, also shown in Figure 1-8a.

Using the celestial equator and poles as reference features, astronomers divide up the surface of the celestial sphere in precisely the same way that the latitude and longitude grid divides Earth. The equivalent to latitude on Earth is called declination (Dec.) on the celestial sphere. It is measured from 0° to 90° north or south of the celestial equator. The equivalent of longitude on Earth is called right ascension (R.A.) on the celestial sphere, measured from 0 h to 24 h (where h denotes hours, the units of angular measurement for right ascension) around the celestial equator (see Figure 1-8a). The boundaries of the constellations, introduced above, run along lines of constant right ascension and constant declination. Because stars are all so far away, their R.A. and Dec. do not change perceptibly over our lifetime (except as measured in modern observatories, which can detect changes for some of the nearer ones).

GUIDED DISCOVERY: The Stars and Constellations

Many students take an introductory astronomy course expecting to be taught the familiar stars and constellations. Often, instructors just do not have time to cover this material. You can, however, learn them on your own in several ways.

First, use the two steps for memorizing the night sky discussed in the text:

1. Observe easily identified constellations.
2. Associate these constellations with nearby, lesser-known stars and constellations.

For example, you may not remember where the star Aldebaran in Taurus is in the sky, but if you remember that Orion is fighting Taurus, you can locate Aldebaran by following a line defined by the belt of Orion to the right (away from Sirius). The first bright star you encounter is Aldebaran.

Make your own connections between the constellations. Have fun while you’re doing it. Chances are that you will remember the phrase “slam the Big Dipper’s bowl downward to hit Leo the Lion on the head” rather than “the first bright group of stars directly below the Big Dipper is Leo.”

Second, astronomy software such as Starry Night™ or Google Sky can provide the star locations and myriad other features of the night sky, including what constellations are up each night; the motion, location, and phases of the Moon and planets; the location of deep sky objects, such as nebulae; and the sky as seen from any location on Earth on any date.

A third way to familiarize yourself with the night sky is to go out on clear nights armed with star charts to see which constellations are up. You will find a set of such charts from the Griffith Observer magazine at the back of this book. To use the charts, first select the one that best corresponds to the date and time of your observation. Hold the chart vertically and turn it so that the direction you are facing outdoors shows at the bottom. The patterns and connections between stars and constellations will soon become evident. Using a flashlight with a red plastic coating over the light will make it easier to read the chart without ruining your night vision. You will find stargazing a truly enjoyable experience.

1-4 An “alt”ernative coordinate system

Just as latitude and longitude can take us any place on Earth, right ascension and declination are a coordinate system for the entire celestial sphere. If you know the R.A. and Dec. for a given object and know how to navigate around the celestial sphere (that is, if you know the angle for the object from the celestial equator and the angle around the celestial equator from the equivalent of prime meridian on the sky), you can find that object’s location in the night sky. The problem is that without lots of experience and/or the appropriate software at hand, figuring out the coordinate system on the night sky and locating that object can be difficult. There is an alternative, local coordinate system that often expedites navigating around the night sky, called the altazimuth or altazimuth coordinate system.

The altazimuth system (Figure 1-8b) depends on your location. It is easy to use: First find the North Pole star, Polaris (see Section 1-2). Facing the direction of Polaris, you are facing due north. Look straight at the horizon below Polaris. This is (0°, 0°) in the altazimuth system. Altitude is the angle straight up from the horizon toward your zenith, the point directly overhead. (Every place has a different zenith.) Altitude runs between 0° at the horizon and 90° at the zenith. The angle to the right of north along the horizon is the azimuth coordinate for your position. For example, the azimuth of east is 90°, while the azimuth of south is 180°. Azimuth ranges from 0° to 360°. Figure 1-8b shows how to find Mizar, the middle star in the handle of the Big Dipper, given its altitude and azimuth at a certain location and time.

Because Earth rotates, every object on the celestial sphere is continuously moving from our perspective, so while their R.A. and Dec. are constant, their altitude and azimuth angles are continually changing. Because software like Starry Night™ can calculate the altitude and azimuth for any object, and because it is very easy to use the altazimuth system, as just described, these coordinates are frequently used in astronomy labs at schools and colleges.

1-5 Earth orbits the Sun in a plane called the ecliptic

Imagine that you could see the stars even during the day, so that you could follow the Sun’s motion through the background constellations throughout the year. (The Sun appears to move among the stars because Earth orbits around it.) From day to day, you would see the Sun trace a straight path on the celestial sphere called the ecliptic. As you can see in Figure 1-9a, the ecliptic makes a closed circle bisecting the celestial sphere. Every year the Sun follows the same course through the sky because Earth follows the same path around it.

Figure 1-9: The Ecliptic (a) The ecliptic is the apparent annual path of the Sun on the celestial sphere. (b) The ecliptic is also the plane described by Earth’s path around the Sun. The planes created by the two ecliptics exactly coincide. Note that the rotation axis through Earth’s poles is tilted 23½° from being perpendicular to the ecliptic.

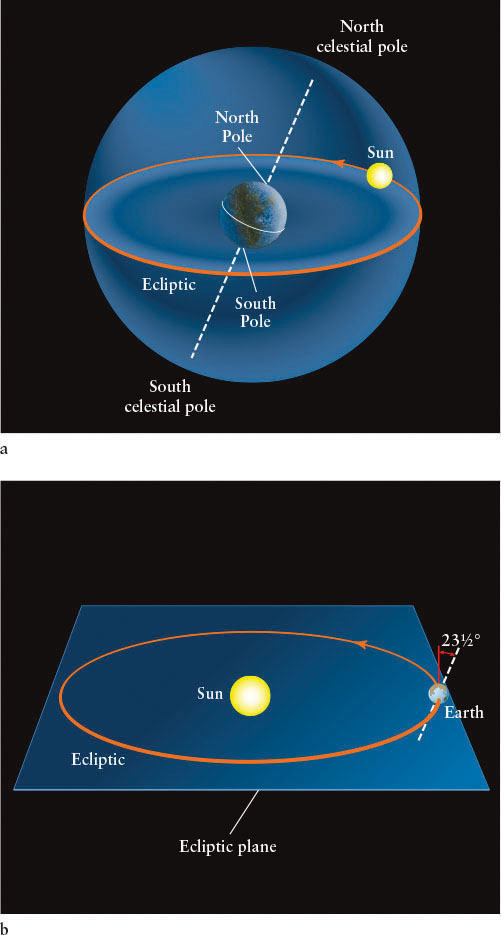
The term “ecliptic” has a second use in astronomy. Earth orbits the Sun in a plane also called the ecliptic (Figure 1-9b). Imagine yourself on the Sun watching Earth move day by day. The path of Earth on the celestial sphere as seen from the Sun is precisely the same as the path of the Sun as seen from Earth. In other words, the plane create by the Sun’s path on the celestial sphere and the plane of Earth’s orbit are identical. Hence, the two ecliptics are the same.

Note in both parts of this figure that Earth’s axis of rotation, running through the North Pole and South Pole, is tilted relative to the ecliptic by 23½°. Because of this tilt, the celestial equator and the path of the Sun around the celestial sphere are tilted with respect to each other by that angle, as shown in Figure 1-8a. Because of this tilt, the two loops meet in two places. Where the Sun is heading northward, this intersection is called the vernal equinox. Halfway around the two circles they meet again at the autumnal equinox. At this time, the Sun is heading southward. Just as the location of Greenwich, England, defines the prime meridian, or zero of longitude on Earth, we need to establish a zero of right ascension. This zero value is defined to be at the vernal equinox (see Figure 1-8a).

In navigating around the celestial sphere, astronomers measure the relative positions of two objects by the angle between them. If you are not familiar with angular separation, read An Astronomer’s Toolbox 1-1: Observational Measurements Using Angles.

AN ASTRONOMER’S TOOLBOX 1-1: Observational Measurements Using Angles

Ancient mathematicians invented a system of angles and angular measure that is still used today to denote the relative positions and apparent sizes of objects in the sky. To locate stars on the celestial sphere, for example, we do not need to know their distances from Earth. All we need to know is the angle from one star to another in the sky, a property that remains fixed over our lifetimes because the stars are all so far away.

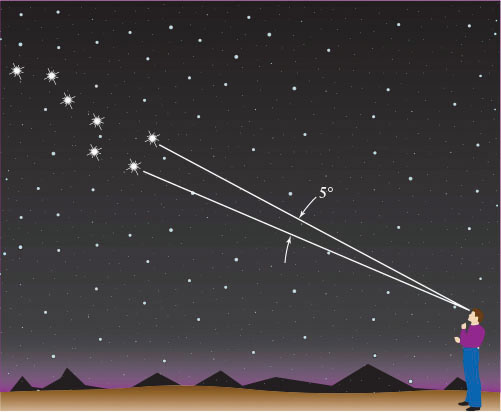
An arc angle, often just called an angle, is the opening between two lines that meet at a point. Angular measure is a method of describing the size of an angle. The basic unit of angular measure is the degree, designated by the symbol°. A full circle is divided into 360°. A right angle measures 90°. As shown in the figure below, the angle between the two “pointer stars” in the Big Dipper is about 5°.

Astronomers also use angular measure to describe the apparent sizes of celestial objects. For example, imagine the full Moon. As seen from Earth, the angle across the Moon’s diameter is nearly ½°. We therefore say that the angular diameter, or angular size, of the Moon is ½°. Alternatively, astronomers say that the Moon “subtends” an angle of ½°. In this context, subtend means “to extend across.”

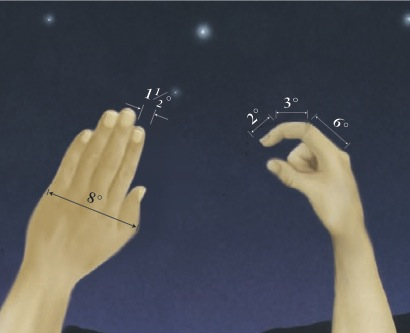
An adult human hand held up at arm’s length provides a means of estimating angles. For example, five fingers extended at arm’s length cover an angle of some 8–10°, whereas the tip of your finger is about 1½° wide. Various segments of your index finger extended to arm’s length can be similarly used to estimate angles a few degrees across, as shown in the figure on the right.

The Big Dipper The angular distance between the two “pointer stars” at the front of the Big Dipper is about 5°. For comparison, the angular diameter of the Moon is about ½°.

Estimating Angles with the Human Hand Various parts of the adult human hand extended to arm’s length can be used to estimate angular distances and sizes in the sky. (These angles vary slightly from person to person because hands and arms are different sizes.)

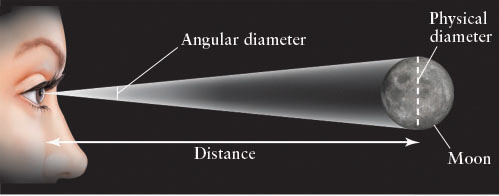
To talk about smaller angles, we subdivide the degree into 60 arcminutes (abbreviated 60 arcmin or 60′). An arcminute is further subdivided into 60 arcseconds (abbreviated 60 arcsec or 60″). A dime viewed face-on from a distance of 1.6 km (1 mile) has an angular diameter of about 2″. From everyday experience, we know that an object looks bigger when it is nearby than when it is far away. The angular size of an object therefore does not necessarily tell you anything about its actual physical size. For example, the fact that the Moon’s angular diameter is ½° does not tell you how big the Moon really is. But if you also happen to know the distance to the Moon, then you can calculate the Moon’s physical diameter. In general, the physical diameter of an object can be calculated from the equation:

physical diameter = distance × tan (angular diameter)

The Physical Diameter of the Moon (or other spherical object in space).

16

where tan (angular diameter) means the tangent of the angle denoted “angular diameter” (see figure). In the Moon’s case, using a measured distance (see Appendix E-3) of 384,400 km and an angular diameter of ½°, we find the diameter to be roughly 3350 km. The difference between this value and the exact diameter of 3476 km is due primarily to the approximate value of ½° that we have used.

Try these questions: The Sun is 1.5 × 10⁸ km away and has a diameter of 1.4 × 10⁶ km. How large an angle does it make in our sky? How does that compare to the arc angle of the Moon in our sky? What arc angle would the Moon make in our sky if it were twice as far away? Half as far?

(Answers appear at the end of the book.)