The Nature of Light
So far in this text we have used the word light in its everyday sense—the stuff to which our eyes are sensitive. This is more properly called visible light, and it is a form of electromagnetic radiation. Perhaps contrary to one’s intuition, this radiation is composed of particles, called photons, that have properties of waves. Detecting electromagnetic radiation with telescopes is the essence of observational astronomy. Although human perception of objects here on Earth and in space comes primarily from the visible light that our eyes detect, visible light is only a tiny fraction of all the electromagnetic radiation emitted by objects in the universe. The rest of this radiation, invisible to our eyes, is detected by hightech sensors attached to specially designed telescopes. In this chapter, we examine telescopes for all types of electromagnetic radiation. To understand how telescopes work, we begin by exploring the properties of the electromagnetic radiation that they collect.
3-1 Newton discovered that white is not a fundamental color and proposed that light is composed of particles
From the time of Aristotle (in the fourth century b.c.e.) until the late seventeenth century c.e., most people believed that white is the fundamental color of light. The colors of the rainbow (or, equivalently, the colors created by light passing through a prism) were believed to be added or created somehow as white light went from one medium through another. Isaac Newton performed experiments during the late 1600s that disproved these beliefs. He started by passing a beam of sunlight through a glass prism, which spread the light out into the colors of the rainbow (Figure 3-1a). The change in direction as light travels from one medium into another is called refraction, and the resulting spread of colors (complete or with colors missing) is called a spectrum (plural, spectra).
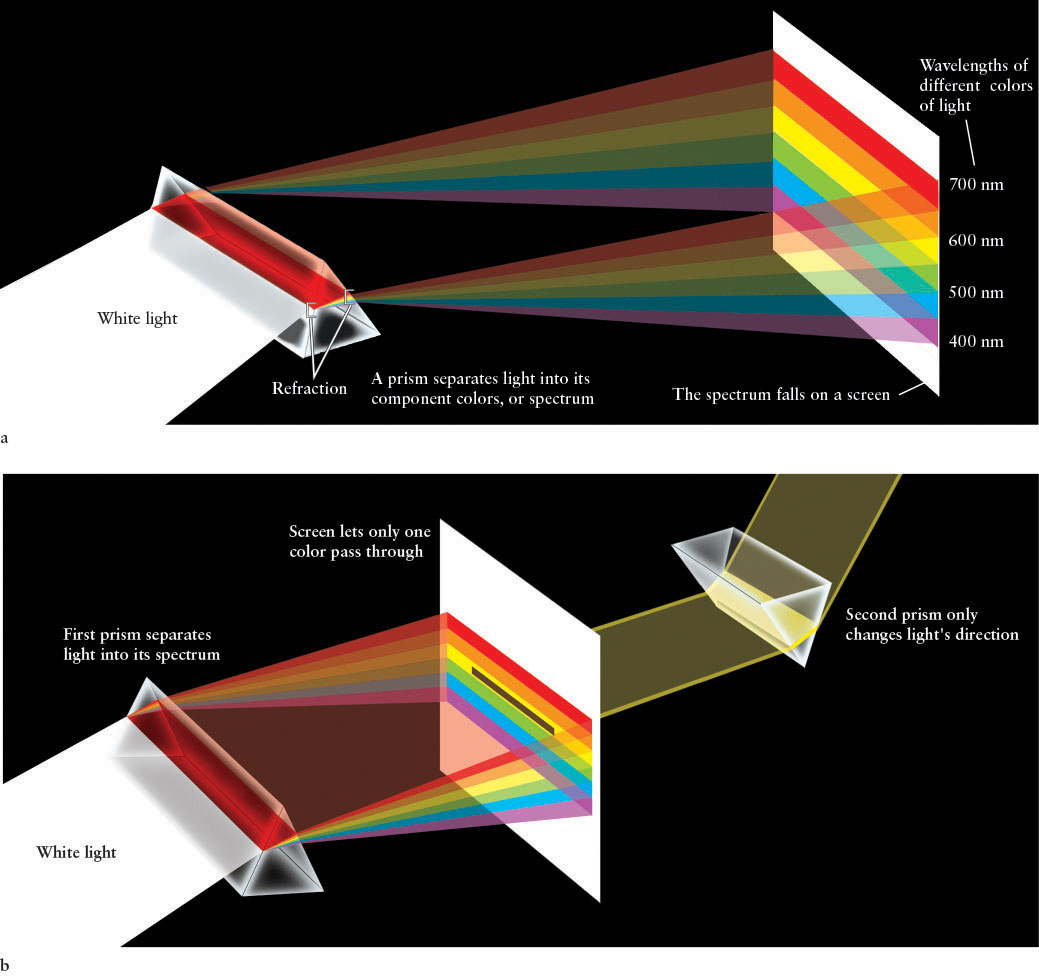
Then Newton selected a single color and sent it through a second prism (Figure 3-1b). The light that emerged from the first prism was refracted by the second prism, but it remained the same color. The fact that individual colors of refracted light were unchanged by the second prism led Newton to conclude that the colors of a full spectrum (shades of red, orange, yellow, green, blue, and violet; indigo is not considered a separate color in astronomy) were in fact properties of the light itself, and that white light is a mixture of colors. To prove this last point, he recombined all the spectrum colors, thereby recreating white light. Thus, different colors of the spectrum are different entities. But what, Newton wondered, is the nature of light that it could break apart into distinct colors and then be completely reconstituted?
Back in the mid-1600s, the Dutch scientist Christiaan Huygens (1629–1695) proposed that light travels in the form of waves. Newton, on the other hand, performed many experiments in optics that convinced him that light is composed of tiny particles of energy. It turns out that both ideas were right.
71
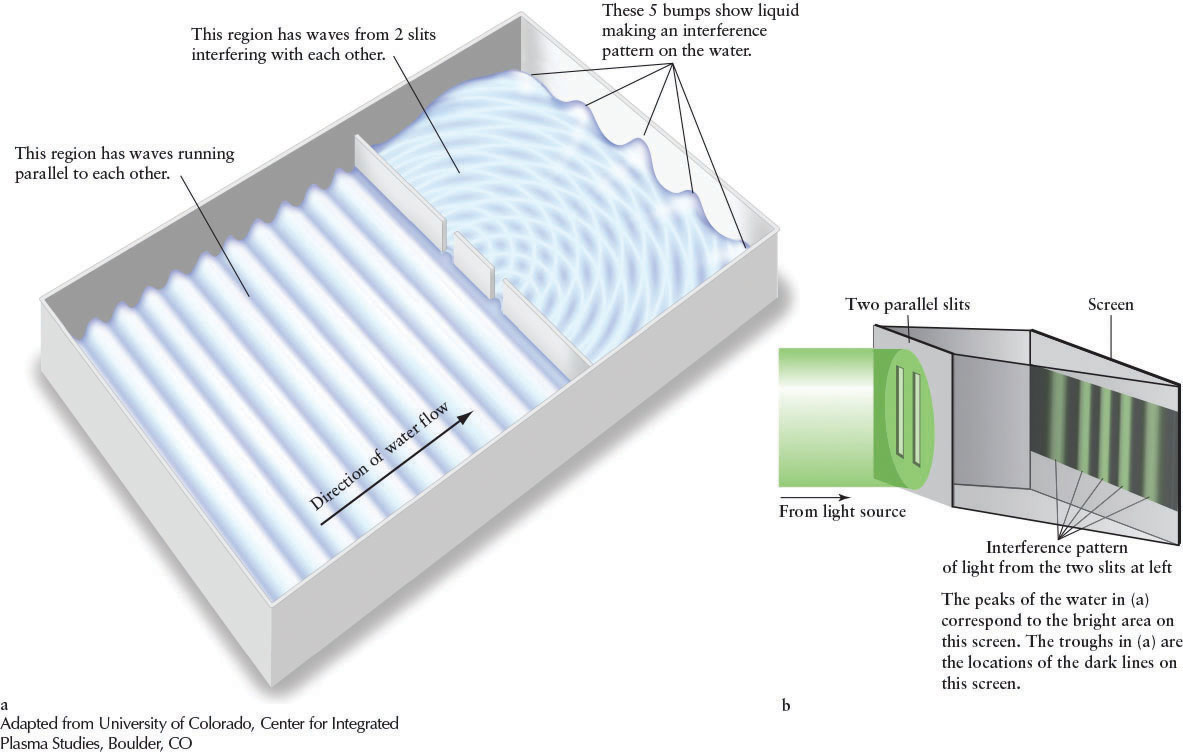
In 1801, the English physicist Thomas Young (1773–1829) demonstrated that light is indeed composed of waves. Young sent light of a single color through two parallel slits (Figure 3-2a). He reasoned that if the light were waves, then these waves would behave the way waves on the surface of water behave, flowing through similar gaps (Figure 3-2b). In particular, he theorized that the light waves from each slit would interact with light waves from the other. For example, when two light waves meet, with one wave going up and the other going down, they would interfere with each other and partially or totally cancel each other out, leaving dark regions on the screen. When two waves that are both moving up or both moving down meet, they would reinforce each other and create bright regions. As you can see in Figure 3-2, this is precisely what happened. (If light were just random particles going through the slits, they would not interfere with each other in this way, and the pattern on the screen would just yield two bright regions, one behind each slit.) The analogy with water waves ends here. For example, light waves do not have to travel through a medium, unlike water waves, which travel through the liquid medium of water.
72
Further insight into the wave character of light came from calculations by the Scottish physicist James Clerk Maxwell (1831–1879) in the 1860s. Maxwell unified the descriptions of the basic properties of electricity and magnetism into four equations. By combining these equations, he demonstrated that electric and magnetic effects should travel through space together in the form of coupled waves (Figure 3-3) that have equal amplitudes. Maxwell’s suggestion that some of these waves, now called electromagnetic radiation, are observed as visible light was soon confirmed by a variety of experiments. Despite the name electromagnetic radiation, neither visible light nor any other type of electromagnetic radiation is electrically charged.
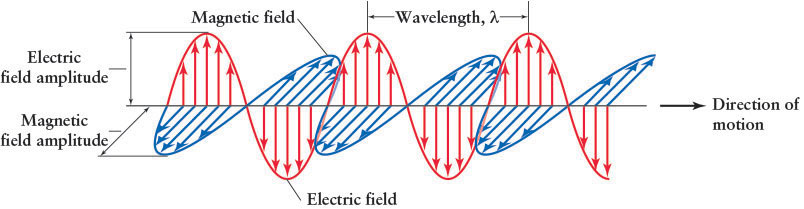
Newton showed that sunlight is composed of all the colors of the rainbow. Young, Maxwell, and others showed that light travels as waves. What makes the colors of the rainbow distinct from each other? The answer is surprisingly simple: Different colors are waves with different wavelengths. A wavelength, usually designated by λ, the lowercase Greek letter lambda, is the distance between two successive wave crests (see Figure 3-3).
The wavelengths of all colors are extremely small, less than a thousandth of a millimeter. To express these tiny distances conveniently, scientists use a unit of length called the nanometer (nm), where 1 nm = 10−9 m. Another unit you might encounter when talking to astronomers is the angstrom (Å), where 1 Å = 0.1 nm = 10−10 m. Experiments demonstrate that visible light has wavelengths ranging from about 400 nm for the shortest wavelength of violet light to about 700 nm for the longest wavelength of red light. Intermediate colors of the rainbow fall between these wavelengths (see Figure 3-1a). The complete spectrum of colors from the longest wavelength to the shortest is red, orange, yellow, green, blue, and violet. Referring to Figure 3-1, you can also see that the amount of refraction that different colors undergo depends on their wavelengths: The shorter the wavelength, the more the light is refracted.
73
3-2 Light travels at a finite but incredibly fast speed
The fact that we see lightning before we hear the accompanying thunderclap tells us that light travels faster than sound. But does that mean that light travels instantaneously from one place to another, or does it move with a measurable speed?
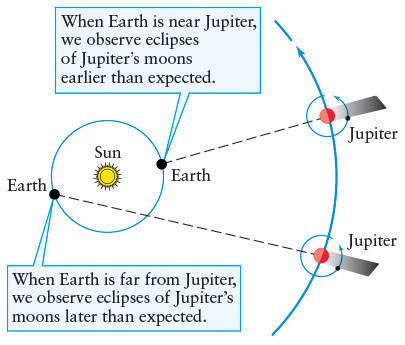
The first evidence for the finite speed of light came in 1675, when Ole Rømer (1644–1710), a Danish astronomer, carefully timed eclipses of Jupiter’s moons (Figure 3-4). Rømer discovered that the moment at which a moon enters Jupiter’s shadow depends on the distance between Earth and Jupiter. When Jupiter is in opposition—that is, when Jupiter and Earth are on the same side of the Sun (see Figure 2-4)—the Earth–Jupiter distance is relatively short compared to when Jupiter is near conjunction. At opposition, Rømer found that eclipses occur slightly earlier than predicted by Kepler’s laws, and they occur slightly later than predicted when Jupiter is near conjunction.
Margin Question 3-1
Question
What color is refracted least?
Rømer correctly concluded that light travels at a finite speed, and so it takes more time to travel longer distances across space. The greater the distance to Jupiter, the longer the image of an eclipse takes to reach our eyes. From his timing measurements, Rømer concluded that it takes 162 minutes for visible light to traverse the diameter of Earth’s orbit (2 AU). Incidentally, Rømer’s interpretation of the data requires a heliocentric cosmology—that both Earth and Jupiter orbit the Sun.
Rømer’s subsequent calculation of the speed of light was off by 25% because the value for the astronomical unit (the average distance from Earth to the Sun) that existed at that time was highly inaccurate. Nevertheless, he proved his main point—light travels at a finite speed. The first accurate laboratory measurements of the speed of visible light were performed in the mid-1800s.
Maxwell’s equations also reveal that light of all wavelengths travels at the same speed in a vacuum (a region that contains no matter), and, despite a few atoms per cubic meter, the space between planets and stars is a very good vacuum. The constant speed of light in a vacuum, usually designated by the letter c, has been measured to be 299,792.458 km/s, which we generally round to
c = 3.0 × 105 km/s = 1.86 × 105 mi/s
(Standard abbreviations for units of speed, such as km/s for kilometers per second and mi/s for miles per second, will be used throughout the rest of this book.) Light that travels through air, water, glass, or any other substance always moves more slowly than it does in a vacuum.
Margin Question 3-2
Question
The speed of sound is about 0.34 km/s (0.21 mi/s). How can this and the information in this section be used to determine a person’s distance from a lightning strike?
The value c is a fundamental property of the universe. The speed of light appears in equations that describe, among other things, atoms, gravity, electricity, magnetism, distance, and time. Light has extraordinary properties. For example, if you were traveling in space at 99% of the speed of light, 0.99c, you would still measure the speed of any light beam moving toward you as c, which is also the speed you would measure for any light beam moving away from you!
74
3-3 Einstein showed that light sometimes behaves as particles that carry energy
 By 1905, scientists were comfortable with the wave nature of light. However, in that year, Albert Einstein (1879–1955) threw a monkey wrench into that theory when he proposed that light is composed of particles that have wave properties, creating what is now called the wave-particle duality. He used this idea to explain the photoelectric effect. Physicists knew that electrons are bound onto a metal’s surface by electric forces and that it takes energy to overcome those forces. Shorter wavelengths of light can knock some electrons off the surfaces of metals, while longer wavelengths of light cannot, no matter how intense the beam of long-wavelength light. Because some colors (or, equivalently, wavelengths) can remove the electrons and others cannot, the electrons must receive different amounts of energy from different colors of light. But how? Einstein proposed that light travels as waves enclosed in discrete packets, now called photons, and that photons with different wavelengths have different amounts of energy. Specifically, the shorter the wavelength, the higher a photon’s energy.
By 1905, scientists were comfortable with the wave nature of light. However, in that year, Albert Einstein (1879–1955) threw a monkey wrench into that theory when he proposed that light is composed of particles that have wave properties, creating what is now called the wave-particle duality. He used this idea to explain the photoelectric effect. Physicists knew that electrons are bound onto a metal’s surface by electric forces and that it takes energy to overcome those forces. Shorter wavelengths of light can knock some electrons off the surfaces of metals, while longer wavelengths of light cannot, no matter how intense the beam of long-wavelength light. Because some colors (or, equivalently, wavelengths) can remove the electrons and others cannot, the electrons must receive different amounts of energy from different colors of light. But how? Einstein proposed that light travels as waves enclosed in discrete packets, now called photons, and that photons with different wavelengths have different amounts of energy. Specifically, the shorter the wavelength, the higher a photon’s energy.
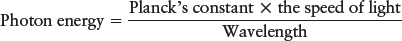
where Planck’s constant (named for the German physicist Max Planck) has the value 6.67 × 10−34 J · s, where J is the unit of energy called a joule (see An Astronomer’s Toolbox 3-1: Photon Energies, Wavelengths, and Frequencies), and the wavelength, the distance between wave crests or troughs, is shown in Figure 3-3. (J · s stands for joules multiplied by seconds, or joule-seconds.) Einstein’s concept of light, confirmed in numerous experiments, means that light can act both as waves (as when passing through slits) and as particles (as when striking matter).
The waves shown in Figure 3-3 are moving to the right. If you count the number of wave crests that pass a given point per second, you have found the frequency of the photon. The unit of frequency is the hertz, named in honor of the German physicist Heinrich Hertz (1857–1894). One hertz means that 1 cycle per second—or that 1 wave crest per second—passes any point. A thousand hertz means a thousand cycles per second, and so on. The frequency is used, among many other things, to identify radio stations. For example, WCPE radio in Wake Forest, North Carolina, has a frequency of 89.7 megahertz (a megahertz is a million hertz or a million cycles per second). Frequency is discussed further in An Astronomer’s Toolbox 3-1.
AN ASTRONOMER’S TOOLBOX 3-1: Photon Energies, Wavelengths, and Frequencies
All photons with the same energy are identical. This energy depends solely on the photon’s wavelength or, equivalently, its frequency. The wavelength, λ, and frequency, f, of a photon are related by the simple equation
c = fλ or, equivalently, f = c/λ
where c is the speed of light. Knowing either the wavelength or frequency, you can calculate the other value with these equations. Also, if you know either of them, you also know the photon’s energy, as introduced in the equation from Section 3-3,
E = hc/λ or E = hf
Planck’s constant, h, is 6.67 × 10−34 J · s and the speed of light, c, is 300,000 km/s.
Example: A photon of red light has a wavelength 700 nm. What is its energy? Note: All distances in the following equation must be converted to the same units, such as meters.

Simplifying, we find Ered = 2.86 × 10−19 J, meaning that each photon of red light with wavelength 700 nm has an energy of 2.86 × 10−19 J.
An aside on units: Just as the numbers in the numerator of an equation multiply together, the numbers in the denominator multiply together, and the resulting numerator is divided by the denominator, so are units combined in the same way. The same units found in both the numerator and denominator cancel. For example, a result such as 7 km s/s would have the seconds cancel on the top and bottom, leaving 7 km as the answer.
Furthermore, in any equation, the units of the same type (such as length) must all be converted to the same standard, so that they can be combined or canceled. In our case, we would convert both nanometers and kilometers to meters, combine the resulting powers of 10, and cancel the units on the top and bottom. For example, 1 km/1 nm = 103 m/10−9 m = 10+12 (with no units). The cancellation of units in the equation left just joules, as it should, because we were calculating an energy.
Compare: In 1 s, a 25-watt lightbulb emits 25 J.
Try these questions: A photon has an energy of 4.90 × 10−19 J. Calculate its wavelength in nanometers. Referring to Figure 3-1: What is this photon’s color? What is the wavelength of a photon with twice this energy? What is the energy of a green photon?
(Answers appear at the end of the book.)
75
All photons with the same wavelength are identical to each other, and, therefore, every photon of a given wavelength carries the same amount of energy as every other photon with that wavelength. The energy delivered by a photon is either enough to eject an electron from the surface of the metal or it is not; there is no middle ground. Extensive testing in the twentieth century confirmed both the wave and particle properties of light.
While the energy of a single photon is fixed by its wavelength, the total number of photons passing per second from that source with a given energy determines the intensity of the electromagnetic radiation at that wavelength (that is, how bright the object appears to be). The more photons detected, the higher the intensity, and vice versa. However, the intensity of light does not change the energy per photon. If one photon is unable to eject an electron from a metal, then billions of photons with that energy will still be unable to remove that electron.
3-4 Visible light is only one type of electromagnetic radiation
We now know that visible light occupies only a tiny fraction of the full range of possible wavelengths, collectively called the electromagnetic spectrum. Visible light has the range of wavelengths from 400 to 700 nm. However, Maxwell’s equations place no length restrictions on the wavelengths of electromagnetic radiation. What lies on either side of this interval? Around 1800, the British astronomer William Herschel (1738–1822) discovered infrared radiation in an experiment with a prism. When he held a thermometer just beyond the red end of the visible spectrum, the thermometer registered a temperature increase, indicating that it was being heated by an invisible form of energy (Figure 3-5). Infrared radiation, discovered before Maxwell’s equations were formulated, was later identified as electromagnetic radiation with wavelengths slightly longer than red light. Our bodies detect infrared radiation as heat.

In experiments with electric sparks in 1888, Hertz succeeded in producing electromagnetic radiation a few centimeters in wavelength, now known as radio waves.
Margin Question 3-3
Question
Which has more energy, an infrared photon or an ultraviolet photon?
At wavelengths shorter than those of visible light, ultraviolet (UV) radiation extends from about 400 nm to 10 nm. In 1895, Wilhelm Roentgen (1845–1923) invented a machine that produces electromagnetic radiation with wavelengths shorter than 10 nm, now called X-rays. Modern versions of Roentgen’s machine are found in medical and dental offices. X-rays have wavelengths between about 10 and 0.01 nm. Photons with even shorter wavelengths are called gamma rays. These boundaries are all arbitrary and primarily used as convenient divisions in the electro-magnetic spectrum, which is actually continuous.
As shown in Figure 3-6, the electromagnetic spectrum stretches from the longest-wavelength radio waves, through microwaves, infrared radiation, visible light, ultraviolet radiation, and X-rays, to the shortest-wavelength photons, gamma rays. On the long-wavelength side of the visible spectrum, infrared radiation covers the range from about 700 nm to 1 mm. Astronomers interested in infrared radiation often express wavelength in micrometers or microns (abbreviated μm), where 1 μm=1000 nm=10−6 m. From roughly 1 mm to 10 cm is the range of microwaves. Microwaves are sometimes considered as a separate class of photons and sometimes categorized as infrared radiation or radio waves. Formally, radio waves are all electromagnetic waves longer than 10 cm.
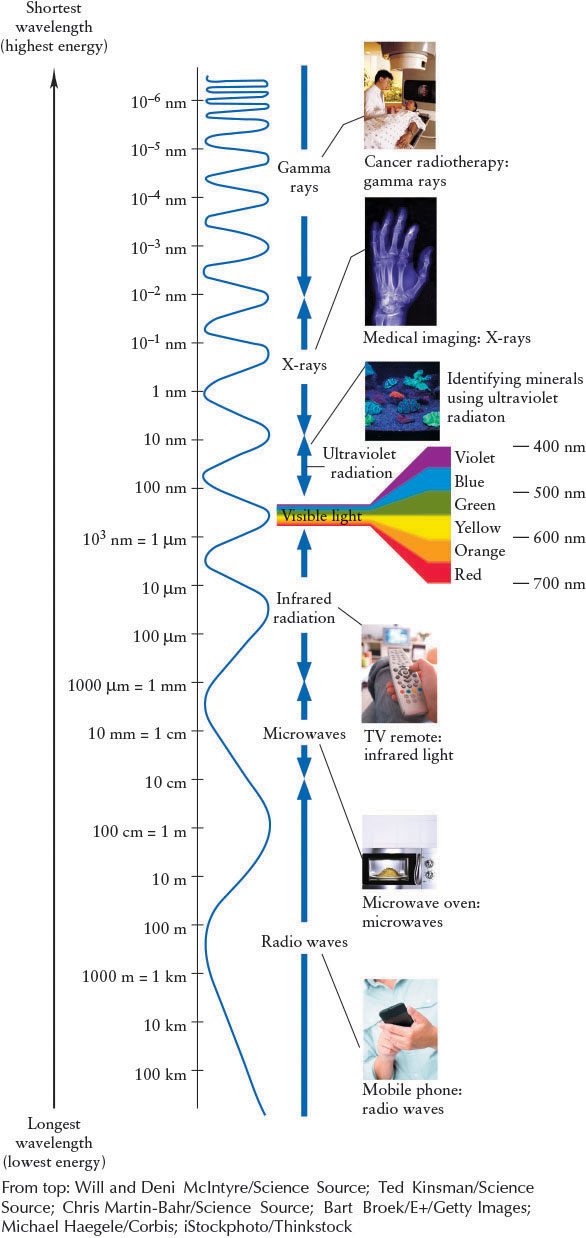
76
The various types of electromagnetic radiation share many basic properties. For example, they are all photons, they all travel at the same speed, and they all sometimes behave as particles and sometimes as waves. But, because of their different wavelengths (and therefore different energies), they interact very differently with matter. For example, X-rays penetrate deeply into your body tissues, while visible light is mostly stopped and scattered by the surface layer of skin; your eyes respond to visible light but not to infrared radiation; and your radio detects radio waves but not ultraviolet radiation.
Earth’s atmosphere is relatively transparent to visible light, radio waves, microwaves, short-wavelength infrared, and long-wavelength ultraviolet. As a result, these radiations pass through the atmosphere without much loss and can be detected by ground-based telescopes sensitive to them. Astronomers say that the atmosphere has windows for these parts of the electromagnetic spectrum (Figure 3-7).

77
The longest-wavelength ultraviolet radiation, called UVA, causes tanning and sunburns. Ozone (O3) in Earth’s atmosphere normally screens out intermediate-wavelength ultraviolet radiation, or UVB. Until recently, the ozone in the ozone layer high in the atmosphere was being depleted by human-made chemicals, such as chlorofluorocarbons (CFCs) and bromine-rich gases. As a result, more UVB is reaching Earth’s surface, and these highly energetic photons severely damage living tissue, causing a surge in the rates of skin cancer and glaucoma, among other diseases.
 Earth’s atmosphere is completely opaque to the other types of electromagnetic radiation, meaning that they do not reach Earth’s surface. (This opacity is a good thing, because short-wavelength ultraviolet radiation [UVC], X-rays, and gamma rays are devastating to living tissue. Gamma rays, packing the highest energies, are the deadliest.) Direct observations of these wavelengths must be performed high in the atmosphere or, ideally, from space.
Earth’s atmosphere is completely opaque to the other types of electromagnetic radiation, meaning that they do not reach Earth’s surface. (This opacity is a good thing, because short-wavelength ultraviolet radiation [UVC], X-rays, and gamma rays are devastating to living tissue. Gamma rays, packing the highest energies, are the deadliest.) Direct observations of these wavelengths must be performed high in the atmosphere or, ideally, from space.
As noted earlier, photons with different energies interact with matter in different ways. Higher-energy photons will pass through or rip apart material from which lower-energy photons will bounce off. Telescope designs for collecting and focusing radiation, therefore, differ depending on the energies or, equivalently, the wavelengths of interest. Knowing the energies of photons and their effects on matter enables astronomers to design telescopes and recording devices sensitive to them. In the next section we will consider the lengths to which astronomers have gone to capture visible and invisible (or nonoptical) electromagnetic radiation.