Atoms and Spectra

An atom is the smallest particle of a chemical element that still has the properties of that element. At the time of Kirchhoff’s discoveries, scientists knew that all matter is composed of atoms, but they did not know how atoms were structured. Furthermore, scientists saw that atoms of a gas somehow extract light of specific wavelengths from continuum spectra that pass through the gas, leaving dark absorption lines, and they perceived that the atoms then radiate light of precisely the same wavelengths—the bright emission lines (see Figure 4-6). But traditional theories of electromagnetism could not explain these phenomena. The answer came early in the twentieth century, with the development of nuclear physics and quantum mechanics.

4-5 An atom consists of a small, dense nucleus surrounded by electrons

The internal structure of atoms first came into focus in 1908 when New Zealand native and 1908 Nobel laureate Ernest Rutherford (1871–1931) and his colleagues at the University of Manchester in England were investigating radioactivity. They were expanding on work done earlier by Polish physicist (and double Nobel laureate, 1903 and 1911) Marie Curie (1867–1934), among others. Over time, a radioactive element naturally and spontaneously transforms into another element by emitting particles. Certain radioactive elements, such as uranium and radium, were known to emit such particles with considerable speed. It seemed plausible that a beam of these high-speed particles would penetrate a thin sheet of gold. Rutherford and his associates found that almost all of the particles did pass through the gold sheet with little or no deflection. To their surprise, however, an occasional particle bounced back (Figure 4-10). It must have struck something very dense indeed.

Figure 4-10: Rutherford Scattering Experiment Most helium nuclei (also called alpha particles) entering a thin foil scatter slightly as they pass through the medium, but some scatter backward, indicating that they have encountered very dense, compact objects. Such experiments were the first evidence that most matter is concentrated in what are now called atomic nuclei.

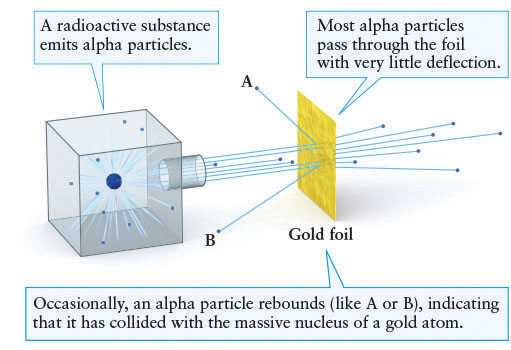
Within a few decades, the structure of atoms became evident. That dense “something” is now called the nucleus of the atom, and it consists of particles called protons and neutrons. Surrounding the nucleus, one or more electrons normally orbit. Newton’s second law (see Section 2-7) explains that electrons move much more than the nuclei they orbit because the electrons have only 1/2000 the mass of a proton or neutron.

Unlike the planets, whose gravitational interaction keeps them orbiting the Sun, electrons orbit nuclei because electrons and protons have a property called electric charge. All protons have the exact same positive charge, while all electrons have a negative charge equal in strength to the proton’s charge. The terms positive and negative are arbitrary and just indicate that the charges are opposite to each other. Particles with opposite charges attract each other. Therefore, protons attract electrons, and it is this attraction that keeps electrons in orbit around nuclei. The interaction between charged particles is a result of the electromagnetic force, the second of four fundamental forces in nature. (Gravitation is the first fundamental force we have discussed.)

Particles with the same type of charge, such as a pair of protons or a pair of electrons, repel each other. For atoms that have more than one proton in their nuclei (and many do), the protons are pushing away from each other. For nuclei to have more than one proton, there must be an attractive force stronger than the repulsion of protons to keep them glued together. The electrically neutral neutrons in the nucleus help provide that attractive force, called the strong nuclear force. This is the third of the four fundamental forces.

Many scientists find it fascinating that all of the interactions between matter and energy in nature occur as a result of just four forces, the above three plus the weak nuclear force. The weak nuclear force is involved in some radioactive decays, such as when a neutron transforms into a proton. In Chapter 18, we will further explore the weak nuclear force in our study of the evolution of the whole universe. The properties of all four fundamental forces are summarized in Table 4-2.

The number of protons in an atom’s nucleus, called the atomic number, determines the element of that atom. All hydrogen nuclei have 1 proton, all helium nuclei have 2, all carbon nuclei have 6 protons, and so forth. There are 92 different types of elements that form naturally. Uranium is the most massive, with 92 protons (see the periodic table in Appendix F). As we will explore in Chapter 13, the fact that neutrons can transform into protons by emitting an electron and that protons can transform into neutrons by absorbing an electron is vital for the formation of elements with more than 26 protons.

In contrast to each atom of a given element always having the same number of protons in their nuclei, the nuclei of most elements can have different numbers of neutrons. For example, hydrogen, with 1 proton, can have 0, 1, or 2 neutrons; oxygen, with 8 protons, can have 8, 9, or 10 neutrons. Each different combination of protons and neutrons is called an isotope. There are three isotopes of hydrogen and three isotopes of oxygen. Hydrogen with no neutrons is the most common hydrogen isotope, while oxygen with 8 neutrons is by far the most abundant isotope of oxygen.

Some isotopes are stable, meaning that the numbers of protons and neutrons in their nuclei do not change. However, many elements have isotopes that are unstable and come apart spontaneously. These isotopes are radioactive, as discussed earlier in this section. For example, carbon with 6 neutrons, ¹²C (“carbon twelve”), is stable, while carbon with 8 neutrons, ¹⁴C (“carbon fourteen”), is unstable. ¹⁴C decays into nitrogen with 7 neutrons, ¹⁴N. To learn how radioactive decay is used to determine the ages of different objects, see An Astronomer’s Toolbox 4-2: Radioactivity and the Ages of Objects. Using radioactive age-dating techniques on the oldest rocks brought back from the Moon, astronomers are able to determine roughly when the Moon formed (4.5 billion years ago). Applying the same technique to space debris found on Earth (meteorites), we can determine that the solar system, consisting of the Sun and everything orbiting it, formed some 4.54 billion years ago.

The number of electrons that orbit an atom is normally equal to the number of protons in its nucleus, thus making the atom electrically neutral. Astronomers denote neutral atoms by writing the atomic symbol followed by the Roman numeral I. For example, neutral hydrogen is written as H I and neutral iron is Fe I.

When an atom contains a different number of electrons than protons, the atom is called an ion. The process of creating an ion is called ionization. Ions are denoted by the atomic symbol followed by a Roman numeral that is one greater than the number of missing electrons. Positively ionized hydrogen (missing its one electron) is denoted H II, while positively ionized iron with seven electrons missing is denoted Fe VIII. Note that negative ions also exist, in which nuclei have more electrons orbiting than they have protons.

Atoms can share electrons and, by doing so, become bound together. Such groups of atoms are called molecules. Molecules are the essential building blocks of all complex structures, including life.

4-6 Spectra occur because electrons absorb and emit photons with only certain wavelengths

Because protons and neutrons have masses about 2000 times greater than the mass of an electron, over 99.95% of the mass of any atom is concentrated in its nucleus. The electron orbits are far from the nucleus, typically 10,000 times farther away than the radius of the nucleus. This immense distance is why you may have heard the statement that matter is mostly empty space.

Be careful not to imagine electrons as miniature planets orbiting the nucleus as a “miniature Sun.” Protons, neutrons, and electrons are not tiny solid bodies. Rather, like photons, they all have both wave and particle properties. The science that accurately describes their complex behavior is called quantum mechanics.

AN ASTRONOMER’S TOOLBOX 4-2: Radioactivity and the Ages of Objects

The isotopes of many elements are radioactive, meaning that the elements spontaneously transform into other elements. Each radioactive isotope has a distinctive half-life, which is the time that it takes half of the initial concentration of the isotope to transform into another element. After two half-lives, a radioactive isotope is reduced to ½ × ½ or ¼ of its initial concentration (see the figure below). Among the most important radioactive elements for determining the age of objects in astronomy is the isotope of uranium with 146 neutrons, ²³⁸U (“U two-thirty-eight”). The half-life of ²³⁸U decaying into lead is 4.5 billion years.

The Transformation of Uranium into Lead This figure shows the rate that 1 kg of uranium decays into lead, as described in the text. The 1-kg sample contains 0.125 kg of uranium after 13.5 billion years.

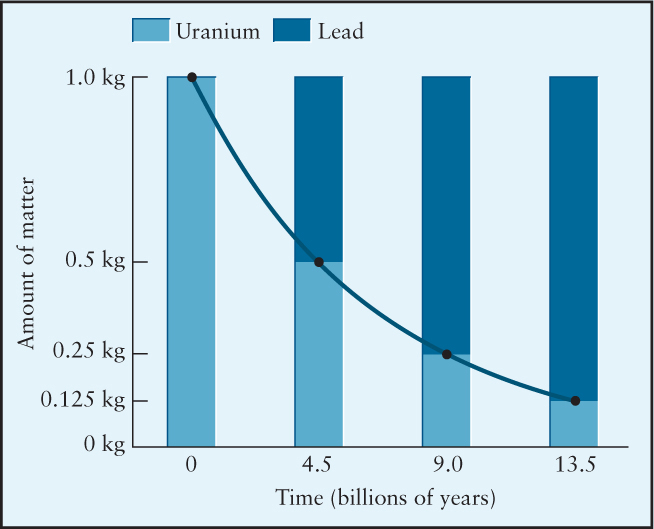
To determine the time since an object, such as a piece of space debris discovered on Earth, solidified, scientists estimate how much lead the object had when it formed. Then they measure the amounts of uranium and lead that it contains now. Subtracting the amount of original lead, they use the amount of uranium and lead, together with the graph of radioactive decay, to determine the object’s age.

Example: Suppose a piece of space debris discovered on Earth was determined to have equal amounts of lead and uranium. How long ago did this debris form? Assuming that it originally had no lead, we see from the chart that a 1-to-1 mix of lead to uranium occurs 4.5 billion years after the object formed. This period is one half-life of uranium.

Compare! This process works with any radioactive isotope. However, some isotopes have such short half-lives that they are not useful in astronomy. For example, the well-known carbon dating used to determine the ages of ancient artifacts on Earth is of little use in astronomy because ¹⁴C has a half-life of only 5730 years. Because so much of the carbon in a sample has decayed away by then, carbon dating is useful only for time intervals shorter than 100,000 years, usually a period over which little of astronomical importance occurs.

Try these questions: What fraction of a kilogram of radioactive material remains after three half-lives have passed? Using the accompanying figure, estimate how much uranium will remain after 6 billion years. Approximately how many half-lives of ¹⁴C pass in 100,000 years?

(Answers appear at the end of the book.)

Quantum mechanics explains that electrons in atoms can exist in only certain allowed orbits around their nuclei, except when they are making a transition from one allowed orbit to another. These orbital conditions are completely unlike planets, which can exist at any distance (in any orbit) around the Sun. Each allowed electron orbit has a well-defined energy associated with it, and every different type of atom and molecule has a unique set of allowed orbits. These orbits and the transitions between them are the key to understanding the spectra that we have been discussing.

Consider an atom of the simplest hydrogen isotope, which contains just a single proton in its nucleus orbited by one electron. (This discussion generalizes directly to all of the other atoms and isotopes, made more complex only because they have more than one electron in orbit.) Figure 4-11 shows this hydrogen atom’s lowest energy levels.

Figure 4-11: Energy Level Diagram of Hydrogen The activity of a hydrogen atom’s electron is conveniently displayed in a diagram showing some of the energy levels, labeled n, at which the electron can exist. A variety of electron jumps, or transitions, are also shown, including those that produce the most prominent lines in the hydrogen spectrum.

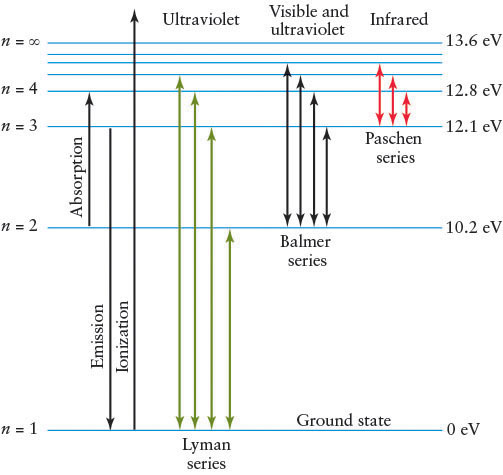
Normally, the electron is in the lowest-energy allowed orbit or energy level, commonly called the ground state; this is labeled n = 1 in Figure 4-11. Each allowed orbit with successively higher energy is labeled n = 2, n = 3, n = 4, and so on. When an electron is in an orbit with more energy than the lowest energy state available to it, it is said to be in an excited state.

Electrons change orbits by absorbing or emitting photons. However, electrons cannot absorb just any photon that they encounter. Electrons can absorb only those photons with energies exactly enough to boost them up to a higher-energy allowed orbit. That is, the photons that are absorbed are those with energies equal to the difference between the energies of two allowed orbits. All photons that do not satisfy this condition pass straight through the atom. If the electron starts in its ground state, then it must get exactly the energy necessary to move it to an excited state. If it is already in an excited state, then by absorbing a photon, it must transition to a higher-energy excited state.

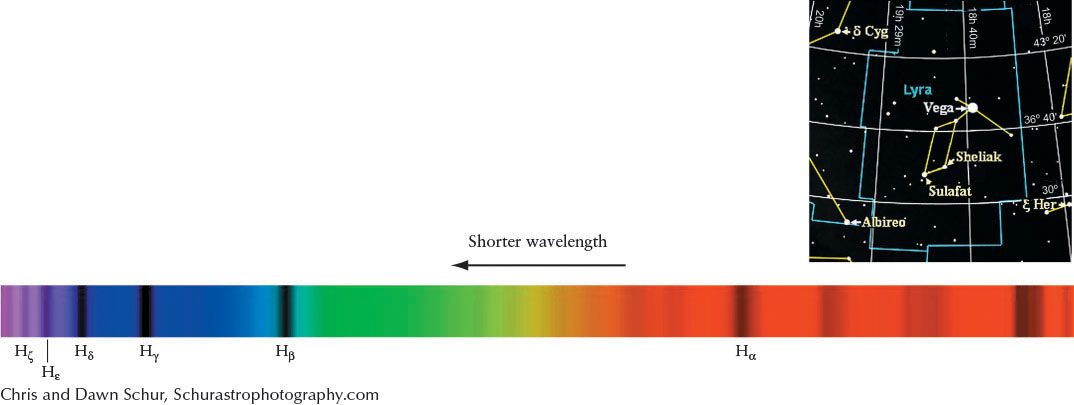
For example, referring to Figure 4-11 and Figure 4-12, transitions between the n = 2 and the n = 3 energy levels require the electron to absorb a photon with energy equal to 12.1 eV − 10.2 eV = 1.9 eV (electron volt, a measure of energy). Recall from An Astronomer’s Toolbox 3-1: Photon Energies, Wavelengths, and Frequencies that a photon’s energy corresponds to a certain wavelength. In this case, the photon absorbed by the electron has a wavelength of 656.3 nm (Figure 4-12a); it is a red photon (recall Figure 3-6).

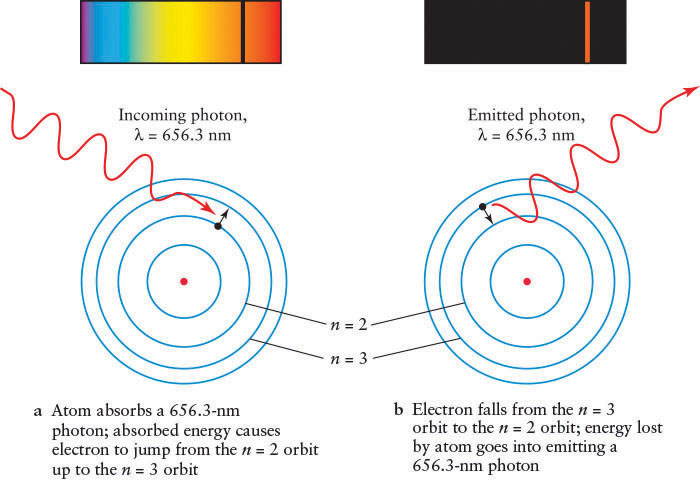
Figure 4-12: The Absorption and Emission of an H_α Photon This schematic diagram of hydrogen’s four lowest allowed orbits shows what happens when a hydrogen atom absorbs or emits an H_α photon, which is red and has a wavelength of 656.3 nm. The spectral lines created by such events are also shown. (a) A photon is absorbed by the electron, causing the electron to transition from orbit n = 2 up to orbit n = 3. (b) A photon is emitted as the electron makes a transition from orbit n = 3 down to orbit n = 2.

Although some absorption occurs at optical wavelengths, it also happens in many other parts of the electromagnetic spectrum. Indeed, most of the transitions in hydrogen, shown in Figure 4-11 as the Lyman series (up from and down to n = 1) and the Paschen series (up from and down to n = 3), are nonvisible photons. Only a few of the Balmer series (up from and down to n = 2) transitions are visible, with the rest being ultraviolet. We will refer to Balmer transitions when we study stars. They are named after the Swiss physicist Johann Balmer (1825–1898), who first calculated their wavelengths in 1885. The longest wavelength Balmer line is called H_α (H alpha), the second H_β (H beta), the third H_γ (H gamma), and so forth, ending with the shortest wavelength Balmer line, H_∞ (H infinity). (The first dozen lines of the series have Greek-letter subscripts; the remainder are identified by numerical subscripts.) Part of the spectrum of a star having Balmer absorption lines H_α through H_θ (H theta) is shown in Figure 4-13.

Figure 4-13: RIVUXG Balmer Lines in the Spectrum of a Star This portion of the spectrum of the star Vega shows six Balmer lines, from H_α at 656.3 nm through H_ζ at 388.9 nm.

Absorption lines are therefore caused by photons being taken out of the stream of light by electrons, which thereby move into higher-energy allowed orbits. An observer on the right in Figure 4-9 looking at the hot blackbody through the cloud of cooler gas sees dark absorption lines where photons have been absorbed by the cooler gas.

Electrons in excited states are unstable. They lose energy by bumping into other particles and suddenly having either too much or too little energy than is necessary to be in that state. When this happens, the electron is forced to descend to a lower-energy allowed state, either the ground state or some allowed state between where it starts and the ground state. In either case, to make this transition down, the electron must emit a photon with energy once again equal to the difference between the energies of the starting and final allowed orbits (see Figure 4-12b).

The emitted photons have the same set of wavelengths as the absorbed photons. Furthermore, the emitted photons are sent out (that is, scattered) in all directions, which creates the glowing emission line spectra of cool gases. The color of a gas depends on the atoms and molecules that it contains. Hydrogen-rich gas clouds glow red because of the H_α emission (Figures 4-13 and 4-14a). Oxygen emits many green photons, so oxygen-rich gas clouds glow green (Figure 4-14b).

Figure 4-14: Emission Spectra from Interstellar Gas Clouds (a) Stars in this interstellar gas cloud (NGC 2363) in the constellation Camelopardus (the Giraffe) emit blackbody spectra. Electrons in the cloud’s hydrogen gas absorb and reemit the red light from these stars. NGC 2363 is located some 10 million ly away. (b) The nebula NGC 604, located 2.7 million ly away in the constellation Triangulum, is also an interstellar gas cloud. The green glow is generated by doubly ionized oxygen atoms (O III; oxygen atoms missing two electrons) in the cloud that emit 501-nm photons. The Rosette Nebula is 3000 ly away.

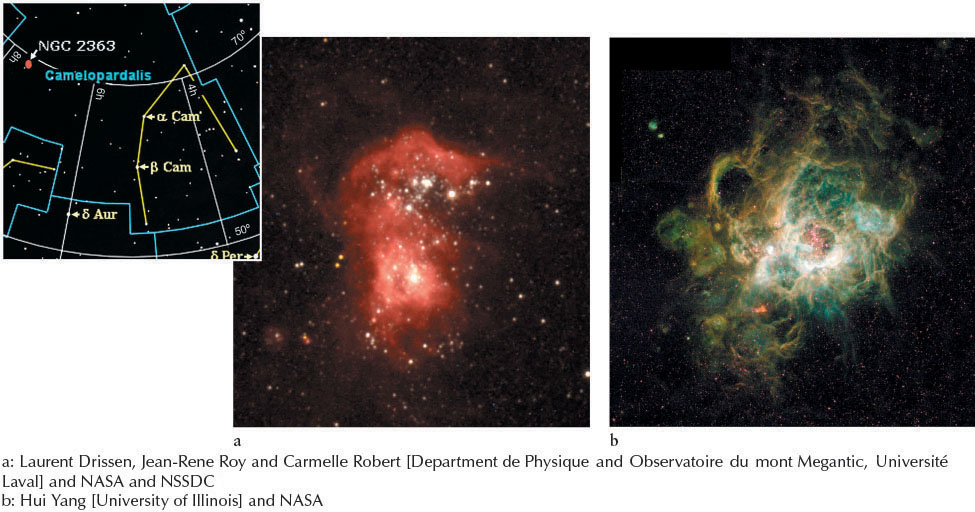
If an electron orbiting in a hydrogen atom encounters a photon with more than 13.6 eV, that photon is absorbed and knocks the electron completely out of orbit and away from the atom. This process is called photoionization. Each type of atom and molecule has a different photoionization energy, above which all electrons are kicked out of the atom or molecule. Photoionization occurs in stars and interstellar nebulae. Indeed, many spectral lines from stars and nebulae are those of ionized atoms that retain at least one electron such as the doubly ionized oxygen atoms in Figure 4-14b.

4-7 Spectral lines shift due to the relative motion between the source and the observer

In 1842, Christian Doppler (1803–1853), a professor of mathematics in Prague, deduced that wavelength, hence color, is affected by motion. As objects move toward or away from you, they change color, in analogy to how the pitch of a siren changes as it passes you. As shown for the observer on the left in Figure 4-15, the wavelengths of electromagnetic radiation from an approaching source are compressed. The circles represent consecutive wave peaks (S₁ through S₄) emitted in all directions as the source moves along. Because each successive wave is sent out from a position slightly closer to her, she sees a shorter wavelength than she would if the source were stationary. All of the colors in the spectrum of an approaching source, such as a star, are therefore shifted toward the short-wavelength (blue) end of the spectrum, regardless of its distance. This phenomenon is called a blueshift.

Figure 4-15: The Doppler Shift Wavelength is affected by motion between the light source and the observer. A source of light is moving toward the left. The four circles (numbered 1 through 4) indicate the location of the peaks of light waves that were emitted by the moving source when it was at points S₁ through S₄, respectively. Note that the waves are compressed in front of the source but stretched out behind it. Consequently, wavelengths appear shortened (blueshifted) if the source is moving toward the observer and lengthened (redshifted) if the source is moving away from the observer. Motion perpendicular to the observer’s line of sight does not affect wavelength.

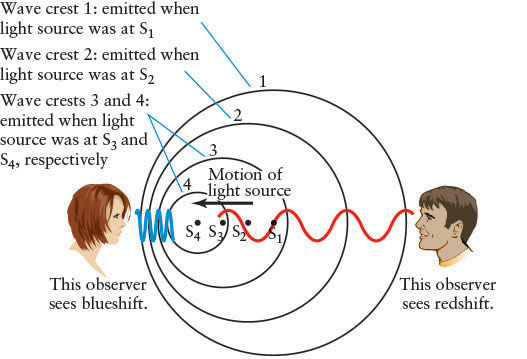
Conversely, electromagnetic waves from a receding source are stretched out. The observer on the right in Figure 4-15 sees a longer wavelength than he would if the source were stationary. All of the colors in the spectrum of a receding source, regardless of its distance, are shifted toward the longer-wavelength (red) end of the spectrum, producing a redshift. A blueshift or a redshift is also called a Doppler shift. The amount of Doppler shift varies directly with approaching or receding speed: When the speeds are small compared to the speed of light, an object that approaches twice as fast as another has all of its colors (or wavelengths) blueshifted twice as much as does the slower-moving object. An object moving away twice as fast as another object has its colors redshifted twice as much as the slower-moving object. Doppler shift applies to spectral lines as well. See An Astronomer’s Toolbox 4-3: The Doppler Shift for mathematical details.

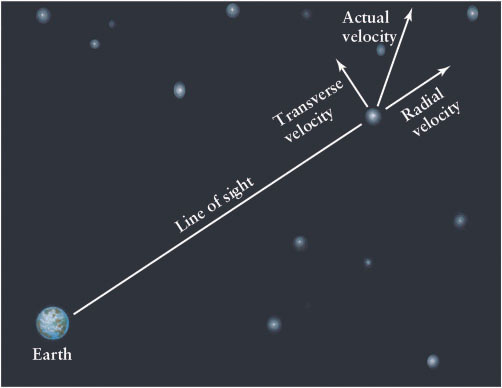
The speed of an object toward or away from us is called its radial velocity (Figure 4-16) because the motion is along our line of sight or, put another way, along the “radius” drawn from Earth to the object. Of course, the star or other object may also have a velocity perpendicular or transverse to our line of sight, like a car passing a pedestrian. Both the radial velocity and the transverse velocity are measured in kilometers per hour.

Figure 4-16: Radial and Transverse Velocities of a Star The actual velocity of a star (or other object) can be separated into radial and transverse motions. The speed of the star toward or away from Earth in kilometers per hour is its radial velocity. This motion creates a Doppler shift in the star’s spectrum. The speed in kilometers per hour perpendicular to the radial velocity is called its transverse velocity, which does not affect the star’s spectrum. The angular motion of the star across the celestial sphere (that is, in the direction of its transverse velocity) is called proper motion.

Astronomers cannot measure the transverse velocity directly. Instead they measure the angle that the body moves among the more distant stars on the celestial sphere, which appear to move much less rapidly than do stars that are closer to us. This angle is called its proper motion and is often a matter of arcseconds per year or arcseconds per century. Proper motion does not affect the perceived wavelength of an object observed here on Earth and so proper motion cannot be determined by Doppler shift. The star with the greatest proper motion as seen from Earth is Barnard’s star (Figure 4-17). Planets moving among the relatively fixed stars on the celestial sphere are examples of bodies that have large proper motions.

Figure 4-17: Proper Motion of Barnard’s Star Three images of Barnard’s star, taken in 1975, 1977, and 1979, show the proper motion of the star during that time. In addition to having the largest known proper motion (10.3” per year), Barnard’s star is one of the closest stars to Earth.

Stellar proper motions are so small that they can be measured for only relatively nearby stars in our Galaxy. However, the radial velocity of virtually every object in space can be determined. Indeed, even the slow motions of rising and sinking gases on the Sun’s surface can be measured by their spectral Doppler shifts. Doppler shift measurements of stars in double star systems give crucial data about the speeds of the stars orbiting each other. Doppler measurements of planets, the Sun, and other stars reveal that many of these bodies are rotating. Rotation is deduced when the Doppler shift shows that half of a surface is heading toward us, while the other half is simultaneously moving away from us. Furthermore, Doppler measurements reveal that all of the very distant galaxies are moving away from us, meaning that the universe is expanding. The spectra of distant galaxies enable us to determine the rate of that expansion. In later chapters, we will refer to the Doppler shift whenever we need to convert an observed wavelength shift into a speed toward or away from us.

With knowledge of spectroscopy, atomic and nuclear physics, and the Doppler shift, we can now list many of the vital properties of matter in space that are directly available to us from telescopic observations. These properties include the chemical compositions of stars, interstellar gas clouds, and other objects; the temperatures of these objects; the rotation of objects in space; the motion of objects toward or away from Earth; the presence of planets and dim companion stars; and the rate at which the universe is expanding. Knowing these properties, astrophysicists have developed and tested models that provide insights into the ages, masses, distances, internal activity, rotation rates, and companion objects of stars, among many other things.

Modern physics was born when Newton set out to understand the motions of the planets. Two and a half centuries later, scientists—including Maxwell, Planck, Einstein, Curie, Rutherford, and Doppler, among many others—discovered the basic properties of electromagnetic radiation and the structures of atoms. As we will see in the following chapters, the fruits of their labors have important implications for astronomy even today.

4-8 Frontiers yet to be discovered

Spectra provide much of what we know about the cosmos. They continue to yield new insights into the chemical composition of the planets, moons, local space debris, stars, interstellar gas and dust, and galaxies. Furthermore, as we obtain more accurate Doppler measurements of objects in our Milky Way Galaxy, in other nearby galaxies, and, indeed, of entire galaxies, we are better able to determine the rate at which the objects in the universe are moving relative to one another. The more we understand of the chemistries and motions of objects in space, the more accurately we are able to explain the evolution of the solar system, stars, galaxies, and the universe.