11.5 11.4 Voting Systems—Without Weights
Voting systems can be established without mentioning weights. In the United States, a bill becomes law when it achieves the support of a majority of the House of Representatives, a majority of the Senate, and the president; or without the president, a two-thirds majority of both houses. (This ignores filibusters, pocket vetoes, etc.) The United Nations Security Council also has a voting system that we will consider in more detail (see Example 21 on page 490).
Instead of using weights, these voting systems describe the winning coalitions directly, usually by specifying minimal winning coalitions. And then a winning coalition is a set of voters that contains one of the specified minimal winning coalitions. The following example is to review the definition of minimal winning coalition (see page 478).
EXAMPLE 19 Minimal Winning Coalitions in the Four-Shareholder Corporation
Minimal Winning Coalitions in the Four-Shareholder Corporation
Example 6 (page 470) was about the Shapley-Shubik index of the corporation with four shareholders, A,B,C,D. it uses the voting system [51:49, 48, 2, 1], and Table 11.7 lists the winning coalitions and their extra votes.
The minimal winning coalitions are those in which each voter is a critical voter: {A,B},{A,C}, and {B,C,D}. These minimal winning coalitions are displayed in Figure 11.1.
| Winning Coalition | Extra Votes | Critical Voters |
|---|---|---|
| Grand coalition | 49 | None |
| {A,B} | 46 | A,B |
| {A,B,C} | 48 | A |
| {A,B,D} | 47 | A,B |
| {A,C} | 0 | A,C |
| {A,C,D} | 1 | A,C |
| {B,C,D} | 0 | B,C,D |
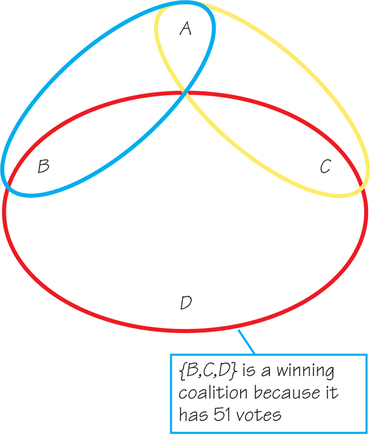
Figure 11.1 shows that every voter belongs to at least one minimal winning coalition.
Self Check 20
What can be said of a voter who doesn’t belong to any minimal winning coalition?
- Suppose X is a voter who belongs to no minimal winning coalition. If X happens to belong to some winning coalition W, then because W is winning, it contains a minimal winning coalition М. We know X does not belong to М, so the coalition formed by removing X from W would still be a winning coalition. This means X has no opportunity to cast a critical vote in any winning coalition: X is a dummy.
Every pair of minimal winning coalitions in Figure 11.1 has some overlap. This is necessary if the voting system is to be decisive, because if two winning coalitions had no overlap, one coalition could pass a motion and the other could pass a contradictory motion.
No minimal winning coalition in the figure is entirely contained in another minimal winning coalition. If there had been a minimal winning coalition, say {A,B,C}, that contained another minimal winning coalition, {A,B} then C would not be a critical voter, since {A,B} can pass a motion without C—hence {A,B,C} would not be minimal.
To describe a new voting system by specifying its minimal winning coalitions, make a list of subsets of the grand coalition that satisfies the following three requirements:
- Your list can’t be empty. You have to name at least one coalition; otherwise, there would be no way to approve a motion.
- You can’t have one minimal winning coalition that contains another one.
- Every pair of coalitions in the list has to overlap.
For dictatorship with dictator D, there would be one minimal winning coalition, {D}. All dictatorships with the same population are the same as voting systems. While we have presented dictatorships as weighted voting systems, the weights are an unnecessary formality.
Self Check 21
Suppose a voting system has just two voters, A and B who are not dummies, and possibly some other voters who are dummies. Can {A} and {B} both be minimal winning coalitions?
- No, {A} and {B} do not overlap.
Equivalent Voting Systems DEFINITION
Two voting systems are equivalent if there is a way for all the voters of the first system to exchange places with the voters of the second system and preserve all winning coalitions.
The weighted voting systems [50:49, 1] and [4:3, 3], involving pairs of voters A, B and C, D, respectively, are equivalent because in each system, unanimous support is required to pass a measure. We could have A exchange places with C, and B exchange places with D. The grand coalition is a minimal winning coalition for each system.
Now consider two voting systems, [2:2, 1] and [5:3, 6], involving the same pair of voters, A and B. In the first, A is a dictator, while in the second, B dictates. By having A and B exchange places with each other, we see that the two systems are equivalent. “Equivalent” does not mean “the same.” Voter A would tell you that the system where he is the dictator is not the same as the system where B is the dictator. The systems are equivalent because each has a dictator.
Every two-voter system is equivalent either to a system with a dictator or to one that requires consensus. As the number of voters increases, the number of different types of voting systems increases.
Now let’s construct some voting systems.
EXAMPLE 20 Three-Voter Systems
Three-Voter Systems
We will make a list of all voting systems that have three participants, A, B, and C. No two voting systems on the list should be equivalent.
Suppose that {A} is a minimal winning coalition. Then A can pass a motion unilaterally and is a dictator. B and C are dummies. Systems where B or C is dictator are equivalent to this one.
If there is no dictator, every minimal winning coalition must contain either two or all three voters. Let’s consider the case in which the grand coalition is a minimal winning coalition. it is the only winning coalition, because any other winning coalition would have to be entirely contained in this coalition, which requirement 2 doesn’t allow. in this voting system, a unanimous vote is required to pass a measure. We will call this system consensus rule.
Finally, let’s suppose that there is a two-voter minimal winning coalition, {A,B}. if it is the only minimal winning coalition, then C is a dummy and A and B make all the arrangements. We will call this system the clique. Of course, the clique could be {A,C} or {B,C}, but these are equivalent systems.
There could be two 2-voter minimal winning coalitions, say {A,B} and {A,C}. Neither coalition contains the other, and there is an overlap, so all of the requirements are satisfied. in this system, A has veto power. We encountered this system in Example 1 (page 463)—where Allen had veto power—and we will call it the chair veto. There are two other voting systems equivalent to this one, where B or C is chair.
It is possible that all three two-member coalitions are minimal winning coalitions. Because there are only three voters, any two distinct two-member coalitions will overlap, so the requirements are still satisfied. This is the majority rule system.
Self Check 22
In general, what can we say about a voter who belongs to all of the minimal winning coalitions?
- Let X be a voter who belongs to all of the minimal winning coalitions. If С is a coalition that X doesn’t belong to, then С contains no minimal winning coalition and is thus a losing coalition. Therefore the vote of X is necessary to win; that is, X has veto power.
Table 11.8 lists all five of these three-voter systems. Each system can be presented as a weighted voting system, and suitable weights are given in the table. If we want to make a similar list of all types of four-voter systems, we can start by changing each three-voter system into a four-voter system, by putting a fourth voter, D, a dummy, into the system. Of course, D would not belong to any of the minimal winning coalitions. You may be interested to know that there are an additional nine 4-voter systems that don’t have any dummies. Try to list as many of these systems as you can.
| System | Minimal Winning Coalitions | Weights | Banzhaf Index |
|---|---|---|---|
| Dictator | {A} | [3:3, 1, 1] | (4, 0, 0) |
| Clique | {A,B} | [4:2, 2, 1] | (2, 2, 0) |
| Majority | {A,B}, {A,C}, {B,C} | [2:1, 1, 1] | (2, 2, 2) |
| Chair veto | {A,B}, {A,C} | [3:2, 1, 1] | (3, 1, 1) |
| Consensus | {A,B,C} | [3:1, 1, 1] | (1, 1, 1) |
EXAMPLE 21 The United Nations Security Council
The United Nations Security Council
The United Nations Security Council has five permanent members—China, France, Russia, the United Kingdom, and the United States—and ten other members that serve two-year terms. To resolve a dispute not involving a member of the Security Council, 9 votes are required, including the votes of each of the permanent members. (Thus, each permanent member has veto power.) The Security Council voting system is thus specified by describing its minimal winning coalitions as consisting of the five permanent members and four other members. Exercise 40 (page 500) is an opportunity to consider this interesting voting system in depth.
EXAMPLE 22 The Scholarship Committee
The Scholarship Committee
A university offers scholarships on the basis of either academic excellence or financial need. Each application for a scholarship is reviewed by two professors, who rate the student academically, and two financial aid officers, who rate the applicant’s need. If both professors or both financial-aid officers recommend the applicant for a scholarship, the dean of admissions decides whether to award a scholarship. Is it possible to assign weights to the professors, the financial-aid officers, and the dean to reflect this decisionmaking system? The answer is no.
To see why, let’s focus on the minimal winning coalitions. The participants are the two professors, A and B; the financial aid officers, E and F; and the dean, D, who has veto power. The minimal winning coalitions (see Figure 11.2) are {A,B,D} and {D,E,F}.
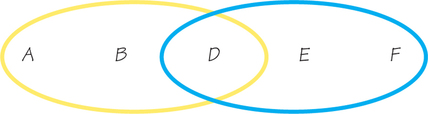
Consider the following two winning coalitions: In C1, all except the financial-aid officer F favors an award; while in C2, Professor B dissents. Thus
C1={A, B, D, E} and C2={A, D, E, F}
In C1, we notice that A is a critical voter and E isn’t, while in C2 the tables are turned because E is critical while A is not. If this were a weighted voting system, then in any winning coalition, the critical voters would all have greater weight than those who are not critical. Thus, A would have to have both more weight than E (because of the situation in C1) and less weight than E (because of C2), which is impossible.
Self Check 23
Let’s change the rules of the scholarship committee: To be approved, an application must receive the votes of at least one professor and both aid officers, or both professors and one aid officer. The dean has veto power, as before. List the minimal winning coalitions. (Exercise 44 on page 500 asks about weighted voting in this version of the committee.)
- There are four minimal winning coalitions; each consists of the dean and three of the other four members.
EXAMPLE 23 Power Indices of the Scholarship Committee
Power Indices of the Scholarship Committee
The dean has veto power. Therefore, she will be the pivotal voter in any permutation where she appears last. If she is second to last in a permutation, she will still be the pivotal voter, because among the three voters before her, there will be either both professors or both financial-aid officers. In the middle position, she will be pivotal if and only if both professors or both aid officers come first. Adding this up, we have 2×4!=48 permutations in which the dean is in fourth or fifth position. There are four permutations of the form Prof, Prof, Dean, Aid, Aid, because the professors and the aid officers can be in either order, and another four of the form Aid, Aid, Dean, Prof, Prof. The dean is not the pivotal voter when she is first or second because at least three people have to approve a scholarship. We conclude that the dean is pivotal in 48+4+4=56 permutations in all. Her Shapley-Shubik power index is therefore 565!=715. Each of the other participants is equally powerful, and they share the remaining 815 of the power. Thus each professor and each aid officer has a Shapley-Shubik power index of 215.
To compute the Banzhaf index, we will make a list of winning coalitions. There are seven of them:
{A, B, D}, {D, E, F}, {B, D, E, F}, {A, D, E, F}, {A, B, D, F}, {A, B, D, E}, and {A, B, D, E, F}
The dean has veto power, so she is a critical voter in each of them. Her Banzhaf power index is therefore 7.
Professor A is a critical voter in {A,B,D}, {A,B,D,E}, and {A,B,D,F}. His Banzhaf power index is 3. The remaining participants have the same power.
In the Shapley-Shubik model, the dean is 312 times as powerful as a faculty member or aid officer. In the Banzhaf model, she is only 213 times as powerful as one of the other members of the Scholarship Committee.