Chapter 12 Exercises
Chapter 12 Exercises
12.1 Narrowing the Field Through the Primary Process
Question 12.29
1. The vote totals for Ann, Bob, and Carl are 6300, 2700, and 1000, respectively. If 19 delegates are to be awarded, then how many delegates does each receive? (Assume that Hamilton’s method of apportionment is used to round the quotas.)
1.
Ann, Bob, and Carl receive 12, 5, and 2 delegates, respectively.
| Candidates | Popular Vote | Percentage of Votes | Percentage after drops | Quota | Initial Delegates | Final Delegates |
| Clark | 14,010 | 12.29 | ||||
| Dean | 33,493 | 29.37 | 43.87 | 3.071 | 3 | 3 |
| Edwards | 13,396 | 11.75 | ||||
| Kerry | 42,847 | 37.58 | 56.13 | 3.929 | 3 | 4 |
| Lieberman | 1,784 | 1.56 | ||||
| Others | 8,507 | 7.46 |
Question 12.30
2. Use the accompanying table and the Democratic Delegate Selection Rules to allocate 19 delegates to Ann, Bob, and Carl. Compare your answer with your answer for Exercise 1.
| Candidates | Popular Vote | Percentage of Votes | Remaining Votes | Adjusted Percentage | Quota | Initial Delegates | Final Delegates |
|---|---|---|---|---|---|---|---|
| Ann | 6300 | ||||||
| Bob | 2700 | ||||||
| Carl | 1000 | ||||||
| Totals | 10,000 |
Question 12.31
3. For the 2004 Democratic primary, only General Clark, Governor Howard Dean, and Senators John Edwards, John Kerry, and Joe Lieberman received a significant number of votes in New Hampshire’s second district. Use the Democratic Delegate Selection Rules to allocate the district’s seven delegates by filling in the following table.
| Candidates | Popular Vote | Percentage of Votes | Percentage after Drops | Quota | Initial Delegates | Final Delegates |
|---|---|---|---|---|---|---|
| Clark | 14,010 | |||||
| Dean | 33,493 | |||||
| Edwards | 13,396 | |||||
| Kerry | 42,847 | |||||
| Lieberman | 1,784 | |||||
| Others | 8,507 |
Question 12.32
4. Calculate the delegate totals for the candidates in Exercise 3, assuming that no cutoff rule was used. Compare your answer with the answer to Exercise 3.
Question 12.33
5. It is possible for every candidate to receive less than 15% of the popular vote. What is the minimum number of candidates for which this can happen?
5.
This can happen with a minimum number of 7 candidates because 1/7<15%, while 1/6>15%.
Question 12.34
6. Under winner-take-all used in the Republican primaries, it is possible for a candidate to win all the delegates from a state but still not have a majority of the popular vote. Suppose that 1001 votes are cast for the 10 candidates. What is the fewest number of votes a candidate could receive and still earn all delegates?
Question 12.35
7. Use Hamilton’s method to allocate eight delegates in both district 1 and district 2 if Candidates Anchor, Barber, and Coachman have the vote totals given in the accompanying table. Compare your answer if instead the 16 delegates were awarded based on the sum of the vote totals for the candidates.
| Candidates | District 1 | District 2 |
|---|---|---|
| Anchor | 55,175 | 47,023 |
| Barber | 45,321 | 23,145 |
| Coachman | 19,112 | 9821 |
7.
Anchor, Barber, and Coachman, respectively, receive 4, 3, and 1 delegates in District 1; 5, 2, and 1 delegates in District 2; and 8, 6, and 2 delegates if the districts are combined.
Question 12.36
![]() 8. Candidates A, B, C, and D receive 44%, 36%, 12%, and 8% of the popular vote, respectively. If Hamilton’s method is used to allocate 100 delegates, how many delegates does each candidate receive? What if a 10% cutoff (instead of the 15% cutoff in the Democratic Delegate Selection Rules) is used? What if a 15% cutoff is used? Suppose that the supporters of Candidate D realize that D will be eliminated and decide to back C instead. How would the allocation of delegates change?
8. Candidates A, B, C, and D receive 44%, 36%, 12%, and 8% of the popular vote, respectively. If Hamilton’s method is used to allocate 100 delegates, how many delegates does each candidate receive? What if a 10% cutoff (instead of the 15% cutoff in the Democratic Delegate Selection Rules) is used? What if a 15% cutoff is used? Suppose that the supporters of Candidate D realize that D will be eliminated and decide to back C instead. How would the allocation of delegates change?
Question 12.37
![]() 9. In Exercise 8, Candidates C and D receive 12 and 8 delegates, respectively. When all the supporters of D vote for C instead, C ends up with 20 delegates. Will it always be the case that, if the votes for the two candidates are combined, the sum of the delegate counts for two candidates is the same as the delegates received? Try constructing a three-candidate example in which eight delegates are awarded and the sum of the delegates awarded to B and to C is different from the number of delegates awarded to the combined Candidate B/C.
9. In Exercise 8, Candidates C and D receive 12 and 8 delegates, respectively. When all the supporters of D vote for C instead, C ends up with 20 delegates. Will it always be the case that, if the votes for the two candidates are combined, the sum of the delegate counts for two candidates is the same as the delegates received? Try constructing a three-candidate example in which eight delegates are awarded and the sum of the delegates awarded to B and to C is different from the number of delegates awarded to the combined Candidate B/C.
9.
No, it is not always the case. Answers will vary for the last part. One such example is when A, B, and C receive 2700, 1000, and 1000 votes, respectively, and 8 delegates are to be awarded. Candidates A, B, and C receive 4, 2, and 2 delegates, respectively, under Hamilton’s method. If candidates B and C are combined, then A receives 5 delegates and the combined B/C receives 3.
Question 12.38
10. Suppose that Hamilton’s method is used to allocate five delegates to Candidates A, B, and C who receive 88%, 9%, and 3% of the vote, respectively. How does your answer change if candidates who do not receive 5% of the vote are eliminated from the election?
Question 12.39
![]() 11. Does your answer to Exercise 10 exhibit the same type of paradoxical behavior as in Example 2? Explain.
11. Does your answer to Exercise 10 exhibit the same type of paradoxical behavior as in Example 2? Explain.
11.
Yes. With no cutoff, Candidate B receives 1 delegate. With a cutoff, Candidate B receives no delegates.
12.2 Spatial Models for Two-Candidate Elections: Discrete Distributions
Refer to the following table for Exercises 12–15.
| Ideal Point | 2 | 4 | 5 | 8 | 9 | 10 | 12 |
| Number of Voters |
2 | 2 | 2 | 5 | 6 | 4 | 2 |
Question 12.40
12. If Candidates A and B announce policy positions of 4 and 10, respectively, then which candidate wins the election?
Question 12.41
13. Given that Candidate B announces policy position 10, what is the best position that Candidate A can announce to maximize votes? How many votes would A receive?
13.
Candidate A’s best position is 9; she would receive 17 votes.
Question 12.42
14. What is the equilibrium policy position? Explain.
Question 12.43
15. If Candidates A and B announce policy positions of 4 and 10, respectively, then how many voters with ideal point 2 would have to be introduced so that A wins the election?
15.
Twelve voters would have to be introduced so that A wins 18 to 17.
Question 12.44
16. A recycling center is to be placed on Main Street. The voters have ideal points between 0 and 10, as given in the following table. As in Example 5, each voter wants the recycling center to be as far away from his or her ideal point as possible. The two proposed sites for the recycling center are 3 and 7. Where will the recycling center be built?
| Ideal Point | 0 | 2 | 3 | 4 | 7 | 10 |
| Number of Voters |
2 | 5 | 4 | 5 | 6 | 7 |
Question 12.45
![]() 17. Prove that if a distribution is discrete and there is no single median position, there is always an extended median.
17. Prove that if a distribution is discrete and there is no single median position, there is always an extended median.
17.
Because there is no median position, there must be an even number of voters. List the ideal positions of the voters in left-to-right/numerical order. Assume that there are 2n voters. Because there is no single median, the nth and (n+1)st ideal positions are not the same. Any position in between these two ideal points has an equal number of voters’ ideal points to both the left and the right. These two ideal points are the endpoints of the extended median.
Question 12.46
18. Twenty voters have ideal points on a left-right spectrum. What is the extended median of the distribution of voters’ ideal points? What is the equilibrium position if an additional voter is added to the distribution with (a) an ideal point of 0.1? (b) An ideal point of 0.4? (c) An ideal point of 0.7? What is the relationship between the equilibrium position and the new voter’s ideal point as it compares with the extended median?
| Ideal Point | 0 | 0.2 | 0.3 | 0.5 | 0.8 | 1 |
| Number of Voters |
2 | 4 | 4 | 6 | 2 | 2 |
Question 12.47
19. Consider two competitive retail businesses, such as department stores, that consider locating their stores somewhere along the main street that runs through a city. Assume that because transportation is costly, people will buy at the store closer to them. Explain how determining a store location is the same as the spatial voting model.
19.
Answers will vary. However, a business wants to be closer to more customers than its rival business.
Question 12.48
20. Extending Exercise 19, assume that there are 100 shoppers at each whole number position from 0 to 10. What is the equilibrium position for the two department stores?
Question 12.49
![]() 21. Because the distribution in Exercise 20 is symmetrical, the median and equilibrium position is for the stores to locate at the center. Indeed, similar stores frequently cluster near the center of many main streets, although these stores may not be particularly convenient to people who live far from the city’s center. The centralized location does not seem to be in the public interest. Wouldn’t it be better if some of the same kinds of stores were near one end of the main street and some near the other? It has been argued that the “social optimum” for the location of the two stores in Exercise 20 should be 2.5 and 7.5, because then no shopper has to travel more than 2.5 from their ideal point. Would the stores still split the shoppers? Explain.
21. Because the distribution in Exercise 20 is symmetrical, the median and equilibrium position is for the stores to locate at the center. Indeed, similar stores frequently cluster near the center of many main streets, although these stores may not be particularly convenient to people who live far from the city’s center. The centralized location does not seem to be in the public interest. Wouldn’t it be better if some of the same kinds of stores were near one end of the main street and some near the other? It has been argued that the “social optimum” for the location of the two stores in Exercise 20 should be 2.5 and 7.5, because then no shopper has to travel more than 2.5 from their ideal point. Would the stores still split the shoppers? Explain.
21.
Yes, because shoppers to the left of 5 would go to the store at 2.5, and shoppers to the right of 5 would go to the store at 7.5. The shoppers at 5 are equidistant between the stores; 50 could go to one and 50 to the other.
Question 12.50
![]() 22. Extending Exercise 19, which is better for consumers: (a) to minimize the maximum distance they must travel to a store or (b) to foster price competition, which would presumably be encouraged if the two stores were located at M=5?
22. Extending Exercise 19, which is better for consumers: (a) to minimize the maximum distance they must travel to a store or (b) to foster price competition, which would presumably be encouraged if the two stores were located at M=5?
Question 12.51
![]() 23. For a two-dimensional policy space, there are four voters with ideal points (1, 0), (0, 1), (−1, 0), and (0, −1). Candidate A announces a policy position of (0, 0). The points are plotted in the accompanying figure. Can Candidate B do any better than to announce (0, 0) as his or her policy position? Explain.
23. For a two-dimensional policy space, there are four voters with ideal points (1, 0), (0, 1), (−1, 0), and (0, −1). Candidate A announces a policy position of (0, 0). The points are plotted in the accompanying figure. Can Candidate B do any better than to announce (0, 0) as his or her policy position? Explain.
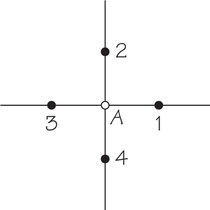
23.
No, B cannot do better. However, B could still get two of the voters to vote for him by announcing a policy position closer to two of the voters. For example, by announcing (12, 12), voters at (1, 0) and (0, 1) would vote for B and the other voters for A.
12.3 Spatial Models for Two-Candidate Elections: Continuous Distributions
Question 12.52
24. Define an outcome to be in equilibrium if, given that one candidate chooses it, the other candidate cannot do better than to take the same position. Show that this definition is equivalent to the text’s definition of being in equilibrium.
Question 12.53
25. Suppose that the continuous distribution of voters’ ideal points is the bent solid line in the accompanying figure. (Note: This is a continuous distribution because the triangle under the bent solid line has area 1.) Assume that A’s policy position is 3 on the left-right continuum; it is denoted by the dashed line. If B announces a policy position between 0 and 1, between 1 and 3, or between 3 and 4, explain which candidate wins the election. What is the median position? Describe which voters vote for B if B announces the median.
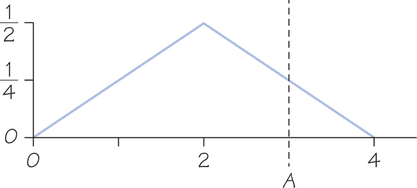
25.
B wins the election if she announces a position between 1 and 3, but loses if she announces positions between 0 and 1 or between 3 and 4. The median is 2. If B announces the median position, then voters between 0 and 2.5 would vote for B.
Question 12.54
26. Consider a symmetric bimodal distribution, which has two peaks of the same height. Will taking a position at either peak be in equilibrium? Explain. (Although this question is for any such distribution, an example is given in Exercise 29.)
Question 12.55
![]() 27. Define A's position in a two-candidate race to be opposition-optimal if, given that the position of B is fixed, it maximizes A's vote total. Show that A's opposition-optimal position must be adjacent to B's position and closer to M, except when B is at the median. (Roughly speaking, being “adjacent” means being a very small distance away.)
27. Define A's position in a two-candidate race to be opposition-optimal if, given that the position of B is fixed, it maximizes A's vote total. Show that A's opposition-optimal position must be adjacent to B's position and closer to M, except when B is at the median. (Roughly speaking, being “adjacent” means being a very small distance away.)
27.
If B’s position is not the median, then A can do no better than to just settle next to B on the side of the median. A’s position should be close enough to B’s position that A’s position is closer to the nearest voter to B’s position that is in between B’s position and the median. This way, A maximizes her vote, getting all voters on the side with the median to vote for her. If B’s policy position is at the median, then A can do no better than to also select the median (by the median- voter theorem).
Question 12.56
28. Along the lines of Exercises 19–21, assume that a distribution of shoppers is given by the graph that accompanies Exercise 25. If Store A locates at 3 (as in the graph) and Store B locates at 1, then no shopper would have to travel more than 1 to go to a store. This notion of a “social optimum” was discussed in Exercise 21. Does the same idea hold for this distribution? Would it be acceptable for shoppers closer to 0 and 4 to travel farther because there are fewer of them?
Question 12.57
29. A continuous distribution of voters’ ideal points is symmetric and bimodal, as illustrated below. Determine the extended median for the distribution. If Candidate A announces a policy position of 2.75, then what is the greatest value that B can announce as a policy position and still be in equilibrium with A? Similarly, what is the least value that B can announce and still be in equilibrium?
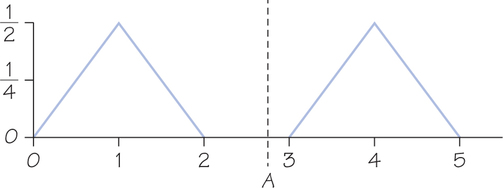
29.
The extended median is [2, 3]. The greatest value that B can announce and still be in equilibrium with A is 3. The least value that B can announce and still be in equilibrium with A is 2.
12.4 Spatial Models for Multicandidate Elections
Question 12.58
30. Assume that there are 11 voters; one voter each has ideal point k for each integer k=0 to 10. Assume that A and B take the same median position. Is there more than one position that C can take to maximize his or her vote total? If so, what are those positions? If not, why not? Can C win the election? Explain.
Question 12.59
31. Assume that there are 10 voters; one voter each has ideal point k for each integer k=0 to 9. Assume that A and B announce policy positions at 4.2 and 5, respectively. Is there more than one position that C can take to maximize his or her vote total? If so, what are those positions? If not, why not? Can C win the election? Explain.
31.
Yes, there is more than one position that C can announce to maximize his or her vote total. For example, the positions 4 and 4.1 both yield 5 votes. C cannot win the election but can tie in the election.
Question 12.60
![]() 32. Assume that A and B take the same nonmedian position. What position should C take to maximize his or her vote total? Is C’s position always a winning one?
32. Assume that A and B take the same nonmedian position. What position should C take to maximize his or her vote total? Is C’s position always a winning one?
Question 12.61
33. Assume that A and B take different positions, with one possibly being at M. What position should C take to maximize his or her vote total? Is C’s position always a winning one?
33.
If, say, A takes a position at M, and B takes a position to the right of M, C should take a position just to the left of M that is closer to M than B’s position, giving C essentially half the votes and enabling him or her to win the election. If neither A nor B takes a position at M, C should take a position next to the candidate closer to M. The position that C takes to maximize his or her vote may be either closer to M (if the candidates are far apart) or farther from M (if the candidates are closer together), but this position may not be winning.
Question 12.62
34. Suppose that 22 voters have the ideal points given in the following table.
| Ideal Point | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of Voters |
2 | 4 | 2 | 2 | 3 | 2 | 3 | 3 | 1 |
If Candidate A announces a policy position of 1 and Candidate B announces a policy position of 7, is there a 2/3-separation opportunity for a third candidate, C, to enter the race? Explain.
Question 12.63
35. Suppose that two voters are added to the distribution given in Exercise 34. Both voters have ideal points at position 5. Is there a 2/3-separation opportunity for a third candidate, C, to enter the race? Explain.
35.
Yes; by announcing a policy position of 4, C could win 9 of the votes, while A and B receive 8 and 7 votes, respectively.
Question 12.64
![]() 36. If the distribution is not symmetric, but no more than 16 of the area under the curve separates A (on the left) from M, and no more than 16 of the area separates B (on the right) from M, is there a 1/3-separation obstacle? What if these 16-or-less areas on the left and the right are not the same?
36. If the distribution is not symmetric, but no more than 16 of the area under the curve separates A (on the left) from M, and no more than 16 of the area separates B (on the right) from M, is there a 1/3-separation obstacle? What if these 16-or-less areas on the left and the right are not the same?
Question 12.65
![]() 37. If the distribution is not unimodal, but at least 13 of the area under the curve separates A (on the left) from M, and at least 13 separates B (on the right) from M, is there a 2/3-separation opportunity? (Hint: Start by assuming that the distribution is uniform between A and B—and hence not unimodal—and that exactly 23 of the voters lie between A and B. Can C always win by taking a position at M? If not, is there a distribution that affords C this opportunity?)
37. If the distribution is not unimodal, but at least 13 of the area under the curve separates A (on the left) from M, and at least 13 separates B (on the right) from M, is there a 2/3-separation opportunity? (Hint: Start by assuming that the distribution is uniform between A and B—and hence not unimodal—and that exactly 23 of the voters lie between A and B. Can C always win by taking a position at M? If not, is there a distribution that affords C this opportunity?)
37.
Following the hint, C will obtain 13 of the vote by taking a position at M, as will A and B, so there will be a threeway tie among the candidates. Because a non-unimodal distribution can be bimodal, with the two modes close to M, C can win if he or she picks up most of the vote near the two modes, enabling C to win with more than 13 of the vote. In this case, Candidate C has taken advantage of a 23-separation opportunity.
Question 12.66
38. If A and B are equidistant from the median of a symmetric distribution and separated from each other by exactly 12 of the area under the curve, under what conditions is this separation an obstacle, and under what conditions is it an opportunity? (Hint: Start by constructing examples of symmetric distributions in which C would either win or lose by taking a position at M.)
Question 12.67
![]() 39. It is known that A, B, and C will enter an election in that order, with A announcing his position first, then B, and finally C. If the distribution is uniform (rectangular) over [0, 1], what position should each candidate take to maximize his or her vote total, anticipating—in the case of A and B—the entry of future candidates? [Hint: Start by assuming that A takes a position at 14. Is B's position at 34 optimal, anticipating the entry of C? Or can B do better at some other position (perhaps by influencing C's choice of a maximizing position)?]
39. It is known that A, B, and C will enter an election in that order, with A announcing his position first, then B, and finally C. If the distribution is uniform (rectangular) over [0, 1], what position should each candidate take to maximize his or her vote total, anticipating—in the case of A and B—the entry of future candidates? [Hint: Start by assuming that A takes a position at 14. Is B's position at 34 optimal, anticipating the entry of C? Or can B do better at some other position (perhaps by influencing C's choice of a maximizing position)?]
39.
B should enter just to the right of 34, making it advantageous for C to enter just to the left of A, giving C essentially 14 of the vote.
Question 12.68
40. Assume that the four candidates in the 2000 presidential election can be arranged from left to right as follows: nader_gore_bush_buchanan. Suppose a poll reveals Gore at 48%, Bush at 47%, Nader at 3%, and Buchanan at 2%. Would Bush be well advised to offer Buchanan a cabinet position to drop out of the race (the same way Adams offered Clay the secretary-of-state post after the 1824 election)? What if Bush knew that, after Buchanan dropped out, only half of Buchanan’s supporters would switch to him, with most of the remainder not voting, except for a few who would switch to Gore?
Question 12.69
41. Assuming the same poll results as in Exercise 40, suppose that Gore offered the same deal to Nader, knowing that only one-third of Nader supporters would switch to him and the rest would not vote. However, suppose Gore also thought that if Nader dropped out, so would Buchanan, and all Buchanan supporters would vote for Bush. Should Gore set off this chain of events?
41.
No, Gore should not set off this chain of events. Gore would receive 1% percent of the electorate (13 of the 3% of voters who prefer Nader). Bush would receive all of 2% of the electorate who vote for Buchanan. Gore and Bush would be tied, each receiving 49% of the electorate.
Question 12.70
![]() 42. Is there any evidence that the four presidential candidates in 2000 might have contemplated “deals” of the kind indicated in Exercises 40 and 41? If you cannot find any evidence, do you think this is because the candidates found such ploys unethical or because they thought they might be found out if they tried to engage in them?
42. Is there any evidence that the four presidential candidates in 2000 might have contemplated “deals” of the kind indicated in Exercises 40 and 41? If you cannot find any evidence, do you think this is because the candidates found such ploys unethical or because they thought they might be found out if they tried to engage in them?
Question 12.71
![]() 43. One tactic that was considered by Nader supporters who thought their votes for Nader might kill Gore’s chances in some states was to swap votes: In close states that Gore might lose if Nader supporters stuck with their candidate, these supporters would switch to Gore if Gore supporters in less contested states, where Gore would almost surely win, would switch to Nader. Thereby, the popular-vote totals for the two candidates would not change overall, but Gore would be able to win in the close states he might otherwise lose. Is this a sensible way of dealing with problems created by the Electoral College, which puts a premium on winning in large states?
43. One tactic that was considered by Nader supporters who thought their votes for Nader might kill Gore’s chances in some states was to swap votes: In close states that Gore might lose if Nader supporters stuck with their candidate, these supporters would switch to Gore if Gore supporters in less contested states, where Gore would almost surely win, would switch to Nader. Thereby, the popular-vote totals for the two candidates would not change overall, but Gore would be able to win in the close states he might otherwise lose. Is this a sensible way of dealing with problems created by the Electoral College, which puts a premium on winning in large states?
43.
Answers will vary. However, such vote trading does not solve problems created by the Electoral College.
12.5 Spatial Models and the Electoral College
Question 12.72
44. Nine states have medians 2, 4, 5, 6, 8, 9, 10, 11, and 12 with associated electoral votes of 10, 8, 4, 4, 2, 3, 5, 5, and 2. Determine an equilibrium position. Is there more than one? Explain.
Question 12.73
45. If states A, B, and C have median positions on a left-right spectrum of 3, 4, and 5, respectively, and the states have 25, 3, and 50 electoral votes, respectively, can the median position of state B ever be the weighted median? Explain. Can you infer anything about how state size impacts elections? Explain.
45.
No, because state C is so large, its median position will always be the median of the three states.
Large states have more influence on the outcome of an election because winning a large state’s electoral votes brings a candidate closer to the majority.
Question 12.74
46. Nine registered voters have ideal points 1, 2, 3, 4, 5, 6, 7, 8, and 9. Suppose two candidates, A and B, have announced policy positions of 4 and 7, respectively. Which candidate wins the election? Candidate B’s strategy is to “get out the vote” by registering more voters with ideal points to the right of the median 5. How many voters must B register to defeat A?
Question 12.75
![]() 47. In Exercise 46, Candidate B was trying to “get out the vote” by registering more voters who would ultimately vote for him or her. There have been attempts to increase political awareness in college-aged students, including an initiative (Rock the Vote!) in which musicians encouraged students to vote. Would Republicans or Democrats benefit the most by such efforts? Why do you think so?
47. In Exercise 46, Candidate B was trying to “get out the vote” by registering more voters who would ultimately vote for him or her. There have been attempts to increase political awareness in college-aged students, including an initiative (Rock the Vote!) in which musicians encouraged students to vote. Would Republicans or Democrats benefit the most by such efforts? Why do you think so?
47.
Answers will vary.
Question 12.76
48. Nine voters have ideal points 1, 2, 3, 4, 5, 6, 7, 8, and 9. Divide the voters into three districts of size 3 such that (a) the median of the medians of the districts is not the median of the nine voters and (b) the median of the medians of the districts is the median of the nine voters.
Question 12.77
![]() 49. Explain how your partition of the voters in Exercise 48a can be used to comment on how the popular-vote winner may not be the Electoral College winner.
49. Explain how your partition of the voters in Exercise 48a can be used to comment on how the popular-vote winner may not be the Electoral College winner.
49.
Answers will vary.
Question 12.78
![]() 50. Assume that a city comprises three equally sized districts, each of which elects a candidate to the city council. The mayor is elected by the entire city. Does this explain why mayors and city council members often disagree? Explain your answer and relate it to the districts in Exercise 48.
50. Assume that a city comprises three equally sized districts, each of which elects a candidate to the city council. The mayor is elected by the entire city. Does this explain why mayors and city council members often disagree? Explain your answer and relate it to the districts in Exercise 48.
Question 12.79
![]() 51. Not every state holds its primary on the same day. Suppose five primaries are held in succession and that delegates are awarded in a winner-take-all manner, in which the candidate with the most popular votes is awarded all the state’s delegates. The primaries of the states 1, 2, 3, 4, and 5 occur in numerical order. If the median of state k is k and each state has the same number of electoral votes, then the median of the entire population is 3. Assume Candidates A and B announce policy positions of 2 and 3.5, respectively. Determine the outcome of each primary. Who should win the combined primary election?
51. Not every state holds its primary on the same day. Suppose five primaries are held in succession and that delegates are awarded in a winner-take-all manner, in which the candidate with the most popular votes is awarded all the state’s delegates. The primaries of the states 1, 2, 3, 4, and 5 occur in numerical order. If the median of state k is k and each state has the same number of electoral votes, then the median of the entire population is 3. Assume Candidates A and B announce policy positions of 2 and 3.5, respectively. Determine the outcome of each primary. Who should win the combined primary election?
The winner of early primaries receives more campaign contributions than the losers of the primaries. These funds can be used to influence the opinion of the voters. Suppose that Candidate A uses the money raised after winning states 1 and 2 in such a way that the electorate in states 3, 4, and 5 believe A’s ads in which Candidate B is portrayed as having a policy position of 4.1. Who wins the election now? Do you believe that money can influence an election in such a way? Explain.
51.
A wins the primaries in states 1 and 2, while B wins the primaries in states 3, 4, and 5 and the primary election. A now wins the primaries in states 1, 2, and 3, as well as the primary election. For questions about money, answers will vary.
Question 12.80
52. Can there be an instance in which it is worse that the candidate with the most (popular) votes (in the country) wins a state election instead of the candidate who wins a majority of the electoral votes? How does the outcome of the 2000 presidential election and Florida’s deciding role relate to the proposed National Popular Vote law? What if the law were passed in enough states?
Question 12.81
53. Assume that the National Popular Vote law is adopted. Would the election winner be the same if there were a direct popular vote (i.e., without the Electoral College) in which the winner is the candidate with the most votes?
53.
Yes, the point of the National Popular Vote law is to elect the direct popular-vote winner.