12.4 12.3 Spatial Models for Two-Candidate Elections: Continuous Distributions
For the spatial models considered so far, there were relatively few voters and their ideal points were known. For a large number of voters, it is impractical to ask each voter to indicate his or her ideal point so that the candidates can determine a median policy position, or a policy position in the extended median. Political candidates use polls to assess the attitudes of individual voters. This information is used to approximate the opinions of the electorate on different issues. Pollsters may represent the discrete distribution of voters by a continuous curve that describes voters’ attitudes on the left-right spectrum.
Continuous Voter Distribution THEOREM
A continuous voter distribution is a curve that gives, on the vertical axis, the number (or percentage) of voters who have attitudes at that point on the left-right continuum.
For simplicity, we picture the distribution as continuous (see Section 8.6), although in fact, because the number of voters is finite, there cannot be voters at all points along the continuum. The analysis of how to select a maximin policy position on the left-right continuum to defeat an opponent is still applicable to the continuous setting.
EXAMPLE 7 A Continuous Distribution of Voters’ Attitudes
A Continuous Distribution of Voters’ Attitudes
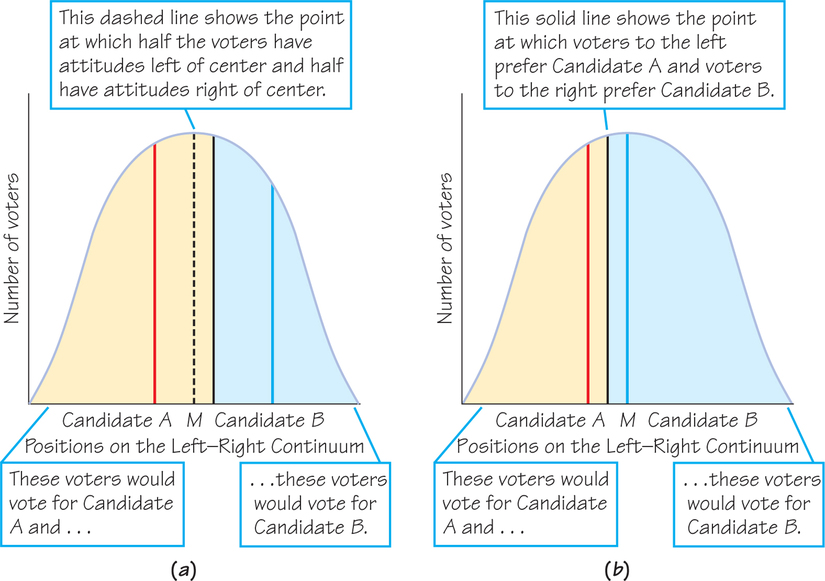
Suppose that voters’ attitudes are described by the continuous distribution over the left-right spectrum given in Figure 12.4a. The red and blue lines represent the policy positions of Candidates A and B, respectively. The voters represented by the tan-shaded area vote for Candidate A; these are voters with ideal points less than and to the left of the midpoint between the policy positions of A and B. The voters represented by the blue-shaded area vote for Candidate B; these are voters with ideal points greater than and to the right of the midpoint between policy positions of A and B. Because of the symmetry of the distribution—which means there is a line in which the distribution looks the same to the left as it does to the right—it is easy to see that more voters vote for A than for B because the tan region is greater in size than the blue region. Hence, A would win the election.
As in the discrete model, there is a maximin position given by the median position of the distribution. For a continuous distribution, a median position covers half the area beneath the curve to the left and half the area beneath the curve to the right. Because the distribution is symmetric, the median position is the middle of the distribution. In Figure 12.4b, B moves to this position—and wins the election! Candidate A has no response to this move and can do no better than to join B at the median.
Median of a Continuous Voter Distribution DEFINITION
The median M of a continuous voter distribution is the collection of points on the horizontal axis where half the area underneath the continuous voter distribution is to the left of M and half is to the right of M.
The median may be a single point or may consist of an interval, as could happen for discrete distributions. If the median is an interval, call it an extended median, as before. Because the median can be defined as before, the median-voter theorem is applicable whatever the distribution of the electorate’s attitudes.
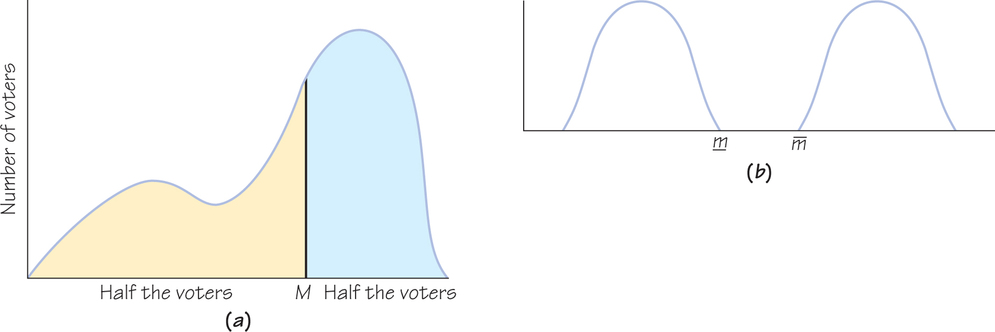
Figure 12.5a shows that one can still find the median for distributions that are not symmetric. The median is marked by M. This means that half the area under the curve is to the left of M and half the area under the curve is to the right of M. Figure 12.5b shows that the notion of an extended median may also be present in a continuous distribution. Any position between m̄ and ˉm, inclusive, is an equilibrium, and the extended median is the interval [m̄, ˉm].
For a discrete distribution, we have already shown that a median M is an equilibrium, which means that if both candidates select M as their policy positions, then neither candidate has an incentive to deviate from this position. The median of a continuous voter distribution is also an equilibrium; that is, if both candidates choose M, these choices are in equilibrium. Suppose there is a unique median position (as opposed to an extended median). Is there another equilibrium position or positions? There are two possibilities: (1) It is the same position for both candidates, which we call a common position, or (2) it is two distinct positions, one taken by each candidate. If it were a common position—suppose it is to the left of M (an analogous argument works if it is to the right)—then one candidate can always do better by moving right but staying to the left of M. This contradicts the supposition that the common position is in equilibrium. Now suppose the equilibrium were two distinct positions. Then one candidate can always do better by moving alongside the other candidate but staying closer to M. This contradicts the supposition that these two positions are in equilibrium.
Thus, in both cases, one candidate would have an incentive to depart from his or her position—holding the position of the other candidate fixed—so a nonmedian position of one or both candidates cannot be in equilibrium. Therefore, M is the only equilibrium position. With an extended median, any pair of policy positions from this set is in equilibrium. A similar argument could be used to show that if one or more of the two positions is outside of this set, then the pair could not be in equilibrium. The notion of the median of a voter distribution is the same as the notion of a median of a data sample given in Section 5.4 (page 196).
Given the stability of the median or the extended median in a two-candidate, single-issue election, is it any wonder that candidates who want to win try to avoid extreme positions? However, if there is a unique median position, and both candidates select it for their policy position, then the candidates become indistinguishable to the voters—and, in the general election, this opens up the door for a third-party candidate to enter the presidential race.