12.5 12.4 Spatial Models for Multicandidate Elections
Spatial modeling can also be used to understand the strategic behavior in multicandidate elections. Once the major parties have selected their candidates, there may be opportunities for third-party candidates to enter the race. Spatial models may also be useful in modeling behavior when there are more than two candidates in primary elections, as many candidates are likely to jump into the fray, especially in the states that go early in the season, if the incumbent president or vice president is not running (as was the case in 2008, when George Bush was unable to run for a third term and Dick Cheney had decided not to enter the Republican primary race).
Under what conditions is it attractive for a third-party candidate to enter the presidential race once the Democratic and Republican candidates have been determined? If no positions offer a potential candidate any possibility of success, then it will not be rational for him or her to enter the primaries in the first place. Therefore, the rationality of entering a race, as well as which position or positions he or she might take once in the race, are really two aspects of the same decision. However, the major party candidates are aware of the possibility of a third-party candidate entering the election. How can the major party candidates prevent a third-party challenger from entering the race?
The median-voter theorem brings the two major party candidates to the middle because the median is a maximin position. If the Democratic and Republican candidates both take positions at M, is there any room for a third candidate?
EXAMPLE 8 Entry of a Third Candidate in a Two-Candidate Race
Entry of a Third Candidate in a Two-Candidate Race
Look at Figure 12.6, in which A and B are both at M and therefore split the vote. If a third candidate, C, enters and takes a position on either side of M (say, to the right), then voters with ideal positions to the right of the midpoint of M and C’s policy position vote for Candidate C. Even though the area under the distribution to C’s right may encompass less than 13 of the total area, C may still win a plurality of votes, that is, more votes than either A or B.
To show why this is so, consider the portion of the electorate’s vote that A/B will receive and the portion that C will receive. If C’s area (tan) is greater than half of A/B’s area (blue), C will win more votes than A or B, because C’s area includes not only the votes to the right of his or her position but also some votes to the left. More precisely, C will attract voters up to the point midway between his or her position on the horizontal axis and that of A/B; A and B will split the votes to the left of this midway point. Because C picks up some votes to the left of his or her position, less than 13 of the electorate may lie to the right and still enable C to win a plurality of more than 13 of the total vote.
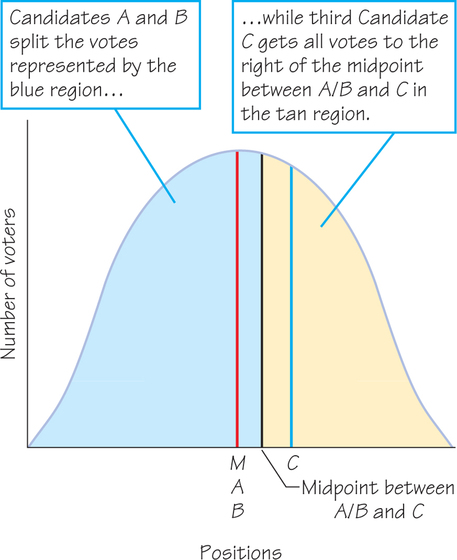
By similar reasoning, it is possible to show that a fourth candidate, D, could take a position to the left of A/B and further chip away at the total of the two centrists. Indeed, D could beat Candidate C, as well as A and B, by moving closer to A/B from the left than C moves from the right.
Clearly, M has little appeal, and is in fact quite vulnerable, to a third or fourth candidate contemplating a run against two centrists. Indeed, it is not difficult to show that whatever positions two candidates adopt—the same or different—at least one of these candidates will be vulnerable to a third candidate.
Self Check 6
Return to the discrete distribution of voters from Example 3. Assume that Ann and Bob both announce the same median policy position of 4. If a third candidate, Carl, announces policy position 5, then all voters with ideal points greater than or equal to 5 vote for Carl; there are 8 such voters. The other 13 voters split between Ann and Bob, say, 6 for Ann and 7 for Bob. Carl wins the election. What is the greatest whole number Carl can announce as his policy position so that he wins a plurality of the 21 votes?
- If Carl announces policy position 7, then voters with ideal points 6 or greater vote for Carl. Carl receives 8 of the 13 votes and wins the election because the other 13 voters split between Ann and Bob.
In Example 8, both Candidates A and B announce policy positions at the median. Even the casual observer of presidential politics would notice that the Democratic and Republican candidates do not run on the same policy platform. Because the major party candidates go through primary processes, their policy positions are closer to the median of the voters in their respective parties, as opposed to the median of the entire population. A candidate may try to adjust his or her position to attract more of the general population but will be unable to simply announce a completely new position. Such a sudden change or perceived change of policy position, often just before or after an election, is referred to as flip-flopping.
Indeed, critics successfully damaged Democratic presidential candidate John Kerry’s chances for being elected, claiming that he had flip-flopped on issues. Famously, Kerry remarked “I actually did vote for the $87 billion, before I voted against it,” when he discussed the Iraq war funding at a campaign appearance— meaning that he supported a Democratic proposal to fund the $87 billion through an elimination of Bush’s tax cuts.
The implication is that just because both major party candidates are trying to attract a plurality—or better, a majority—of the electorate, the candidates’ positions may not be at the median. The entrance of a third-party candidate does not assure that this candidate will win the election. There are obstacles and opportunities for a third-party candidate, which are summarized in Figure 12.7. (The reasoning behind these is explored in Exercises 34 and 35 on page 533.)
1/3-Separation Obstacle DEFINITION
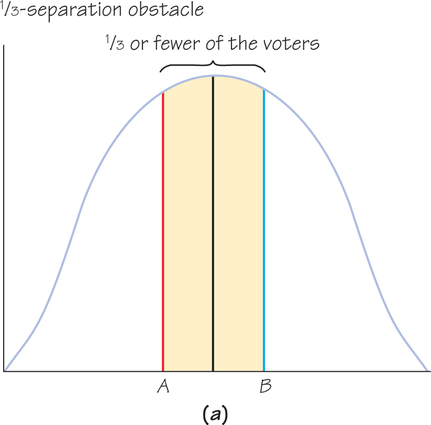
For two candidates, A and B, with previously announced policy positions, the 1/3-separation obstacle occurs when there is little room in the middle between the positions of A and B, enabling C to beat A or B but not both.
2/3-Separation Opportunity DEFINITION
The 2/3-separation opportunity occurs when there is a wide separation between A and B, giving enough room in the middle for C to win.
The 1/3-separation obstacle theorem on the next page is stated for the case in which the continuous distribution of voters is symmetric about the median and has the candidates equidistant from the median. A similar statement for more general distributions can be made, but it requires more detailed hypotheses. For this reason, the more intuitive version is presented. The case in which Candidates A and B are both positioned at the median (as in Example 8) is not a counterexample to the theorem because Candidates A and B are required to have distinct policy positions.
When a continuous distribution of voters has a highest point or peak, it is referred to as unimodal. For a symmetric distribution to be unimodal, the highest peak must occur at the median. This means that more voters have their ideal points closer to the median than farther from the median.
The 2/3-separation opportunity theorem given on the next page requires the continuous distribution of voters to be symmetric about the median and to be unimodal. Again, this assumption makes the result more intuitive.
The 1/3-Separation Obstacle and the 2/3-Separation Opportunity THEOREM
The 1/3-separation obstacle. If A and B are distinct positions that are equidistant from the median of a symmetric distribution and separated from each other by no more than 13 of the area under the curve (so that no more than 13 of the voters lie between A and B), C can take no position that will displace both A and B and enable C to win (see below).
The 2/3-separation opportunity. If A and B are distinct positions that are equidistant from the median of a symmetric unimodal distribution and separated from each other by at least 23 of the area under the curve (so that at least 23 of the voters lie between A and B), C can defeat both A and B by taking a position at M (exactly between them, as shown below).

Both portions of the theorem can be proved by considering the outcome if a Candidate C were to announce a policy position either to the left of A’s policy position, between the policy positions of A and B, or to the right of B’s policy position in Figure 12.7. For example, in Figure 12.7a, a Candidate C with policy position to the left of A’s policy position would capture the voters to the left of A’s policy position. Although Candidate C would receive more votes than Candidate A, Candidate B would still receive half the votes—those of all voters with ideal points to the right of the median.
Self Check 7
Suppose that Candidate C announces a position between the policy positions of Candidates A and B in Figure 12.7a. Explain why C will not win the election.
- If all voters with ideal points between the policy positions of A and B voted for C, then less than 1/3 of all the voters would vote for C. Because A and B are equidistant from the median and the distribution is symmetric, A and B split the remaining votes. Both A and B receive more votes than C.

The 1912 presidential election provides a real-life instance of a third-party candidate entering the race: Theodore Roosevelt ran as the Progressive (“Bull Moose”) Party candidate after losing the Republican nomination to William Howard Taft. (Roosevelt had previously been president but had lost favor with his party after sitting out one term.) In the general election, Roosevelt received 27% of the popular vote and Taft 24%. The Democratic candidate, Woodrow Wilson, who got 41% of the popular vote, handily defeated both candidates. There was a fourth candidate in this race, socialist Eugene V. Debs, but he received only 6% and was never a serious threat to Wilson. Wilson was also the overwhelming winner in the Electoral College. This situation illustrates a 1/3-separation obstacle, as opposed to a 2/3-separation opportunity, in that the third-party candidate was unable to garner enough support to win the election.
In fact, there has never been a third-party candidate who has won an election for U.S. president. Again, the 1912 election is notable, as it was the only election in which a third-party candidate received enough of the popular vote to defeat even one of the major-party candidates.
The stability of the two-party system in the United States may be partially explained by the fact that the two major parties, anticipating the possible entry of a third-party candidate, deliberately position themselves far enough away from the median to discourage entry on the left or right—but not so far away as to make entry in the middle advantageous. Another hypothesis is that the major-party candidates naturally are positioned on either side of the median from their positioning in their primary elections and that their efforts to appeal to as many voters in the general election leads them as close to the median of the general population as possible, leaving scant room in the middle for a challenger to be successful.
Presidential politics in the United States seems to be a reflection of both the median-voter and the 1/3-separation obstacle theorems. For example, the median-voter theorem seems to have been operative in 1968, when the Democratic and Republican nominees, Hubert H. Humphrey and Richard M. Nixon, both presented themselves as centrists. This made them vulnerable to the third-party candidate that year, George Wallace—not in the sense that Wallace could win, but rather that he could throw the election in one direction or the other, or even into the House of Representatives to be decided. In fact, while Wallace won only 14% of the popular vote in 1968, he attracted mostly supporters of Richard M. Nixon, who barely defeated Hubert H. Humphrey (Nixon won by less than 1% in the popular vote). Without Wallace in the race, polls show that Nixon’s victory would have been far more substantial.
In 1992, Bill Clinton and George Bush were viewed as quite far apart on the left-right spectrum. Ross Perot was generally viewed to be between Clinton on the left and Bush on the right, leaving considerable room in the middle that Perot could better exploit than by trying to displace one of the major-party nominees on the left or right. In winning 19% of the popular vote, Perot drew almost equally from each candidate. However, he did not come close to winning, because there was not enough room between Clinton and Bush for there to be a 2/3-separation opportunity. (Clinton won decisively, with 43% of the popular vote to Bush’s 38%.)
Up to now, we have looked at the spatial game that candidates play as they vie to position themselves optimally in two-candidate and multicandidate races so as to (1) receive a plurality of the vote or (2) deter new candidates from entering. We will continue to assume that candidates take positions along a left-right spectrum, but now we consider the effect of one or more of the candidates dropping out of the election.
Assume that three candidates take positions, from left to right, as follows: A–. Clearly, if or drops out, their supporters mostly likely will switch to , giving the centrist a boost. But what if is the first to drop out? Then it is unclear whether , , or neither will benefit; it depends on the number of ’s supporters who prefer next, next, or neither (and hence may not vote at all). In any event, with out of the race, the winner must be one of the candidates on the extremes.
The possibilities become more interesting when there are four candidates arranged from left to right as follows: . If one of the extremists, or , drops out, then one of the two centrists, or , will benefit. But what if a centrist, say , drops out? Does this benefit one of the extremists, or does the other centrist benefit? At first glance, one might think that, with only one centrist remaining, he or she will surely benefit. This will not be the case, however, if most supporters prefer to , which is certainly possible. Then the extremist will benefit, which will be most upsetting to ’s supporters. Conceivably, ’s supporters might encourage to withdraw so that they can throw their support to , whom they definitely prefer to .
Does this sound implausible? Think back to the 2000 election, in which our four hypothetical candidates are replaced by the following ordering from left to right: Nader-Gore-Bush-Buchanan. (Ralph Nader was the Green Party candidate on the left and Pat Buchanan the Reform Party candidate on the right.) Just before the election, the polls were showing that Buchanan was not much of a threat to Bush, but Nader—who ended up with 2.7% of the popular vote nationwide (Buchanan got only 0.4%)—was definitely a threat to Gore. Despite pleas from some of his supporters, Nader refused to withdraw and, consequently, gave Bush a victory in Florida and maybe a few other close states that won him the presidency.
This 2000 scenario is not the same as the previous four-candidate hypothetical scenario, in which we argued that the extremist on the right, , might win if one of the centrists, , dropped out. In the 2000 scenario, the extremist on the left, Nader, could have dropped out to “save” the centrist closer to him, Gore. Unfortunately for Gore, Nader not only refused to make this sacrifice but contended afterward that Gore’s loss was due to Gore’s own poor performance, not Nader’s presence in the race. We assumed that it was rational for a candidate to enter a race when he or she has a possibility of winning the election. However, a candidate may be less concerned about representing the public and instead may be interested in promoting an agenda. Among other issues, Nader supported campaign finance reform, the environment, universal healthcare, increasing the minimum wage, and the abolition of the three-strikes laws. Despite Nader’s belief that Gore was responsible for losing to Bush, Nader’s role in the 2000 election was that of a spoiler.
Spoiler DEFINITION
A spoiler is a candidate who cannot win but “spoils” the election for a candidate who otherwise would win.