14.1 The Apportionment Problem

1. Jane has decided to track her daily expenses and finds them to be as listed in the table. Express these as percentages. If rounded to whole numbers, do the percentages add up to 100 percent?

2. A mathematics department uses 20 teaching assistants to aid in its four-semester calculus course. The number of teaching assistants assigned to each level of the course depends on enrollment. Here are the fall enrollments:

How many teaching assistants should be assigned to each level of the course?

3. Should the mathematics department in Exercise 2 revise the assignments for its TAs? Grades have been posted for the previous semester, and some students need to repeat the previous level of the course. A total of 45 students move from Calculus II to Calculus I, 41 students move from Calculus III to Calculus II, and 12 students move from Calculus IV to Calculus III.

614

4. Here is a typical apportionment problem. Round the numbers in the following sum to whole numbers:

The rounded numbers must add up to 40. How would you approach this?

5. How would you round the numbers in the following sum to whole numbers? The rounded numbers must add up to 60.

14.2 The Hamilton Method

6. Use the Hamilton method to round the numbers in the following sum to whole numbers. The sum of the rounded numbers must be the same as the original sum.

7. Repeat Exercise 6 with the following sum:

8. The 37th pearl. Three friends have bought a bag guaranteed to contain 36 high-quality pearls for $14,900 at an auction. Abe contributed $5900, Beth’s contribution was $7600, and Charles supplied the remaining $1400. After taking the bag to your house, they pour the 36 pearls from the bag onto the kitchen table.

9. A country has three political parties, and it allots seats in its 102-seat parliament by the Hare (Hamilton) method proportionately to the number of votes each receives. In a recent election, the Pro-UFO Party received 254,000 votes, the Anti-UFO Party got 153,000 votes, and the Who Cares Party polled 103,000 votes. Show that two of the parties are tied.

10. A small high school has one mathematics teacher who can teach a total of five sections. The subjects that she teaches, and their enrollments, are as follows: Geometry, 52; Algebra, 33; and Calculus, 12. Use the Hamilton method to apportion sections to the subjects.

11. Repeat Exercise 10 using the following enrollments: Geometry, 77; Algebra, 18; and Calculus, 20.

12. Use the Hamilton method to express the summands of the following expression as whole number percentages of the total:

Repeat the calculation for the following sum:

Do you see a paradox?

13. Abe, Beth, Charles, and David have decided to invest in rare coins. A dealer has offered to sell them a parcel containing 100 identical coins for $10,000. Each person invests all that he or she can afford, but there is not quite enough money, so Charles asks his Aunt Esther to join the group. The coins will be apportioned by the Hamilton method. Here are the amounts invested:

To see how this situation works out with a different apportionment method, refer to Exercise 31 on page 616.

14. The new states paradox. The census of 1900 recorded the following apportionment populations:

The house size was 386. Apportionment was by the Hamilton method.

15. A country has five political parties. Here are the numbers of votes each received in a recent election: 5,576,330; 1,387,342; 3,334,241; 7,512,860; and 310,968. Seats in its parliament are apportioned by the Hare (Hamilton) method. Calculate the apportionments for house sizes of 89, 90, and 91. Does the Alabama paradox occur?

14.3 Divisor Methods

16. Explain why the tentative Webster apportionment of a state with quota is .

17. Reapportion the classes in Exercise 11 (page 614), using the Jefferson method.

18. Reapportion the classes in Exercise 10 (page 614), using the Webster method.

19. The three friends who bought the pearls (see Exercise 8 on page 614) ask you to suggest a different apportionment method to distribute their purchase. Before answering, determine the apportionments given by the Jefferson and Webster methods for the 36- and 37-pearl house sizes, and then make your suggestion.

20. The three friends in Exercise 8 have bought a lot of 36 identical diamonds, at a total cost of $36,000; Abe’s investment was $15,500, Beth’s was $10,500, and Charles’s was $10,000. They decided to apportion the diamonds using the Webster method, and they can’t make it work out. Can you help?

21. A country has a 20-seat parliament. Seats are apportioned to parties by the d’Hondt method. The following table displays the results of a recent election. Make a d’Hondt table and determine the number of seats allocated to each party.

22. Referring to the voting data in Exercise 21, make a Sainte-Laguë table to apportion the parliament.

23. Make a Sainte-Laguë table and apportion the first 30 seats.

24. In Example 14 (page 593), we used a d’Hondt table to apportion the first 30 seats. The Centrists did not get any of the first 30 seats. Which of seats 31-100 will be the first one that the Centrists receive?

25. Which will be the first seat that the Centrists receive if the Sainte-Laguë table is used to apportion the seats?

26. Explain why the population paradox cannot occur if a divisor method of apportionment is used. (If one state receives an increased apportionment even though its population decreased, how did the divisor used in the second apportionment differ from the divisor used in the first one?)

27. Explain why the new states paradox (see page 585) cannot occur if a divisor method of apportionment is used. (Would the divisor used in the apportionment after the new state joined the union have to be different from the divisor used before?)

28. Round the following to whole percentages using the Hamilton, Jefferson, and Webster methods:

Do any of these apportionments show a violation of the quota condition?

29. Round the following percentages to whole numbers, using the methods of Hamilton, Jefferson, and Webster.

Do any of these apportionments show a violation of the quota condition?

30. Use the Webster method to apportion the House of Representatives, based on the census of 1790. Choose a divisor such that each state’s district population is greater than 30,000, and as many seats as possible are apportioned.

31. Recalculate the apportionment of the coins in Exercise 13 (on page 614) by the Webster method. Again, after the excise tax is paid, a coin changes hands. Who gives it to whom?

32. A country has two political parties, the Liberals and the Tories. The seats in its 99-seat parliament are apportioned to the parties according to the number of votes they receive in the election. If the Liberals receive 49% of the vote, how many seats do the Liberals get with the Hamilton (Hare) method? With the Webster (Sainte-Laguë) method? With the Jefferson (d’Hondt) method?

33. A country with a parliamentary government has two parties that capture 100% of the vote between them. Each party is awarded seats in proportion to the number of votes received.

14.4 Which Divisor Method Is Best?

34. A barista uses 11 grams of coffee to make an espresso and 16 grams to make a doppio. Find the percentage difference in the amounts of coffee used for the two drinks.

35. Jim is 72 inches tall and Alice is 65 inches tall. What is the percentage difference in their heights?

36. Find the Hill-Huntington rounding points for numbers between 0 and 1; between 1 and 2; between 2 and 3; and between 3 and 4.

37. A high school has one math teacher who can teach five sections. A total of 56 students have enrolled in the algebra class, 28 have signed up for geometry, and 7 students will take calculus. Use the Hill-Huntington method to decide how many sections of each course to schedule.

38. One year later, the high school described in Exercise 37 still has just one math teacher who teaches 5 sections. The enrollments are algebra, 36; geometry, 61; and calculus, 3. Apportion the classes by the Webster and Hill-Huntington methods. Which apportionment do you think the school principal would prefer?

39. In 2001, Utah sued to increase its apportionment (Utah v. Evans). Federal employees stationed abroad are counted in the apportionment population of the state of their residence, and Utah wanted to include in its apportionment population religious missionaries who were based in the state and serving abroad.

40. (a) Show that for any positive numbers and , the geometric mean is less than the arithmetic mean,⁵ except when ; in that case, the two means are equal. (Hint: Show that the triangle in Figure 14.2 is a right triangle.)

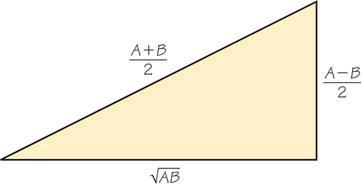
(b) If is a number such that the Webster and Hill-Huntington roundings of differ, show that is greater than the Hill-Huntington rounding point and is less than the Webster rounding point . Conclude that, in this case, the Hill-Huntington rounding of is equal to and the Webster rounding is equal to .

(c) Explain why the fact established in part (b) implies that the Hill-Huntington method is more favorable to small states than the Webster method.

41. A city has three districts with populations of 100,000, 600,000, and 700,000, respectively. Its council has 20 members, and seats on the council are apportioned by the Hill-Huntington method according to the district populations. Show that there is a tie. Would a tie occur with any of the other apportionment methods that we have considered?

42. In a 1991 federal lawsuit, Massachusetts v. Mosbacher, Massachusetts claimed that the Hill-Huntington method of apportionment is unconstitutional because it does not reflect the “one person, one vote” principle as well as the Webster method does. Would Massachusetts have gained a seat from Oklahoma if the Webster method had been used to apportion the House of Representatives in 1991? In your calculation, use the following populations and Hill-Huntington apportionments: Massachusetts was apportioned 10 seats for a population of 6,029,051, and Oklahoma was apportioned 6 seats for a population of 3,157,604.

43. In 1822, Congressman William Lowndes of South Carolina proposed an apportionment method, which was never used. Lowndes started, as Hamilton did, by giving each state its lower quota. But where Hamilton apportions the remaining seats to the states whose quotas have the largest fractional parts—in other words, the states for which the absolute difference between the quota and the lower quota is greatest—Lowndes gives the extra seats to the states where the percentage difference is greatest, increasing the apportionments of as many states as necessary to their upper quotas to fill the House.

44. Let the populations of states and be and respectively. The apportionments will be and . Assuming that district populations for state are larger than district populations for state , show that the percentage difference in district populations is

Also show that same expression is equal to the percentage difference in representative share. Hence the percentage difference in district populations is equal to the percentage difference in representative shares.

45. John Quincy Adams, the sixth president of the United States, proposed that the House of Representatives should be apportioned by a divisor method based on the rounding rule that rounds each fraction up to the next whole number.

46. The choice of a divisor method for ?4P apportioning classes to subjects according to enrollments, as in Example 2 (page 577), depends on what the school principal considers most important.

47. Let be the quotas for states in an apportionment problem, and let the apportionments assigned by some apportionment method be denoted . The absolute deviation for state is defined to be ; it is a measure of the amount by which the state’s apportionment differs from its quota. The maximum absolute deviation is the largest of these numbers. Explain why the Hamilton method always gives the least possible maximum absolute deviation.

Chapter Review

48. The Legis County Board of Supervisors has 145 seats and a total population of 115,275. The county is divided into five townships, whose populations are as follows:

Use the Webster method to determine the apportionment of seats on this Board, then repeat, using the Hamilton method. Are the results the same?

49. The Legis County Board of Supervisors (see Exercise 48) has too many seats for its space in the County Administration building. It has decided to use the Jefferson method of apportionment, with 3000 as divisor.

50. Responding to objections raised against the apportionment scheme in Exercise 49, the Legis County Board of Supervisors has adopted the Webster method of apportionment, with 3000 as the divisor.

51. A county has five townships and elects a 301-seat board of supervisors, using the Webster method of apportionment. The populations of the townships are as follows:

52. Considering the problem of apportioning goods to people according to financial contributions, as in Exercise 8 on page 614 (allocating pearls bought at auction) or Exercise 13 on page 614 (rare coins), list the pros and cons for each of the apportionment methods listed below. Considerthe appropriateness of the following standards of comparison: paradoxes, quota condition, bias favoring small or large states, district population equity, representative share equity, and percentage equity.