Skills Check
![]() Skills Check
Skills Check
Question 15.1
1. In the following two-person zero-sum game, the payoffs represent gains to row Player I and losses to column Player II.
[373861594]
What is the maximin strategy for Player I?
- Play the first row.
- Play the second row.
- Play the third row.
1.
c
Question 15.2
2. In Skills Check 1, the minimax strategy of Player II is to play the _________ column.
2.
third
Question 15.3
3. In the following two-person zero-sum game, the payoffs represent gains to row Player I and losses to column Player II.
[293764158]
What is the minimax strategy for Player II?
- Play the first column.
- Play the second column.
- Play the third column.
3.
a
Question 15.4
4. In Skills Check 3, the maximin strategy for Player I is to play the _________ row.
4.
second
Question 15.5
5. Does the game in Skills Check 1 have a saddlepoint? What about the game in Skills Check 3?
5.
Yes; no
For Skills Check Questions 6-11, consider the following three two-person zero-sum games, where the payoffs represent gains to the row Player I and losses to the column Player II.
[3654][−1320][6565142−185750262]
Question 15.6
6. Do any of the above games have a saddlepoint?
6.
Yes, the last game has a saddlepoint.
Question 15.7
7. In which two games does neither player have a dominant strategy?
- The first two games
- The last two games
- The first and third games
7.
a
Question 15.8
8. How many of Player I’s strategies are dominated in the third game?
8.
Three
Question 15.9
9. Which strategy of Player II is dominant in the third game?
- Strategy 1
- Strategy 2
- Strategy 4
9.
c
Question 15.10
10. Strategy _________ of Player I is dominant in the third game.
10.
3
Question 15.11
11. The third game has
- no saddlepoint.
- one saddlepoint.
- more than one saddlepoint.
11.
c
Question 15.12
12. If a game has a saddlepoint, then _________ is the value of the game.
12.
its payoff
Question 15.13
13. In the game of Matching Pennies, Player I wins a penny if the coins match; Player II wins a penny if the coins do not match. Given this information, it can be concluded that the 2×2 matrix representing this game has
- two −1s and two 1s.
- four 1s.
- four −1s.
13.
a
Question 15.14
14. A mixed strategy uses randomization to ___________________.
14.
prevent a player from being exploited by always choosing a pure strategy
Question 15.15
15. Which of these games does not have a saddlepoint?
- Tic-tac-toe
- Chess
- Poker
15.
c
Question 15.16
16. A game is fair if its saddlepoint is equal to __________.
16.
0
Question 15.17
17. In the following game of kicker-versus-goalie, the kicker’s likelihood of being successful in kicking certain goals is given in the game matrix. Recall that the kicker can kick to the goalie’s left GL or the goalie’s right GR and the goalie can dive to the left L or to the right R.
| Goalie | |||
|---|---|---|---|
| L | R | ||
| Kicker | GL | 0.2 | 0.7 |
| GR | 0.8 | 0.3 | |
Which is the best strategy for the kicker?
- Always kick the ball to the goalie’s left.
- Always kick the ball to the goalie’s right.
- Kick the ball equally often to the goalie’s left and to the goalie’s right.
17.
c
Question 15.18
18. In Skills Check 17, the goalie’s optimal strategy is to dive to the left with probability p. What is p?
18.
0.4
Question 15.19
19. In Skills Check 17, if the kicker and the goalie use their optimal mixed strategies, then, on average, the kicker successfully kicks a goal with probability _________.
19.
0.5
Question 15.20
20. In Skills Check 17, if the kicker uses her optimal strategy, do you know beforehand whether she will kick the ball to the goalie’s left or to the goalie’s right? (Yes or No)
20.
No
Question 15.21
21. In the following game of batter-versus-pitcher in baseball, the batter’s batting averages are given in the game matrix. The batter tries to maximize his batting average while the pitcher tries to minimize the batter’s batting average; this is a zero-sum game. The pitcher decides between throwing a fastball and a curveball. When the batter is in the batter’s box, he guesses which pitch is coming (either a fastball or a curveball). If he guesses correctly, then his batting average is higher. For example, it is easier for him to hit a fastball when he correctly guesses that one is coming. However, if he guesses incorrectly, then his batting average goes down.
| Pitcher | |||
|---|---|---|---|
| Fastball | Curveball | ||
| Batter | Fastball | 0.350 | 0.250 |
| Curveball | 0.100 | 0.500 | |
- If the pitcher always pitches a fastball, what should the batter do?
- If the pitcher always pitches a curveball, what should the batter do?
- If the batter always guesses fastball, what should the pitcher do?
- If the batter always guesses curveball, what should the pitcher do?
21.
(a) Guess fastball (b) Guess curveball (c) Pitch curveball (d) Pitch fastball
Question 15.22
22. For Skills Check 21, find the optimal mixed strategy for the batter. Using this strategy, the batter will guess fastball with what probability?
22.
0.8
Question 15.23
23. In Skills Check 21, the pitcher’s exact optimal strategy is to ____________.
23.
pitch fastballs and curveballs each with 12 probability
Question 15.24
24. In the following game of batter-versus-pitcher in baseball, the batter’s batting averages are given in the game matrix.
| Pitcher | |||
|---|---|---|---|
| Fastball | Curveball | ||
| Batter | Fastball | 0.250 | 0.350 |
| Curveball | 0.200 | 0.500 | |
- If the pitcher always pitches a fastball, what should the batter do?
- If the pitcher always pitches a curveball, what should the batter do?
- If the batter always guesses fastball, what should the pitcher do?
- If the batter always guesses curveball, what should the pitcher do?
24.
(a) Guess fastball (b) Guess curveball (c) Pitch fastball (d) Pitch fastball
Question 15.25
25. In Skills Check 24, the pitcher’s optimal strategy is to _______.
25.
pitch fastball
Question 15.26
26. In Skills Check 24, given your answer to Skills Check 25, the optimal strategy for the batter is to ______.
26.
guess fastball
Question 15.27
27. Consider the following partial-conflict game with ordinal payoffs (in which a player rank-orders the outcomes 1, 2, 3, and 4).
| Player II | |||
|---|---|---|---|
| Choice A | Choice B | ||
| Player I | Choice A | (4, 4) | (1, 3) |
| Choice B | (3, 1) | (2, 2) | |
Both players might select B because ___________.
27.
selecting B is optimal if the other player selects B
Question 15.28
28. In Skills Check 27, what strategy constitutes a Nash equilibrium?
- Only when both players select A
- Only when both players select A or both select B
- Only when one player selects A and the other selects B
28.
b
Question 15.29
29. In the following game, Player I has the preferences of the row player in the Prisoners’ Dilemma, and Player II has the preferences of the column player in Chicken.
| Player II | |||
|---|---|---|---|
| Choice A | Choice B | ||
| Player I | Choice A | (3, 3) | (1, 4) |
| Choice B | (4, 2) | (2, 1) | |
Does the player with a dominant strategy benefit more than the player without one?
- Yes
- No
- It doesn’t make any difference; both players do equally well by choosing strategies associated with the Nash-equilibrium outcome.
29.
a
Question 15.30
30. In Skills Check 29, the strategies associated with (4, 2) constitute a Nash equilibrium, but those associated with (3, 3) do not because ____________.
30.
Player I prefers Choice B to Choice A
Question 15.31
31. A game tree is used to
- determine the possible strategies of a player.
- anticipate each other’s choices through backward induction.
- plan a deception strategy.
31.
b
Question 15.32
32. Suppose that Chicken is played sequentially instead of simultaneously. Use backward induction to determine the equilibrium outcome for the game tree for Chicken.
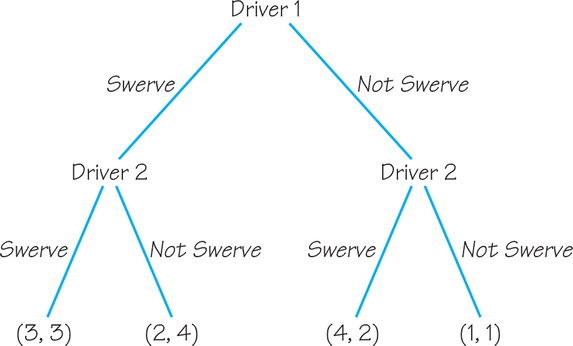
32.
The equilibrium outcome is for Player I to Not Swerve and for Player II to Swerve.