16.2 16.1 Check Digits
Look at the 13-digit International Standard Book Number (ISBN) printed on the back cover of this book. The number 978-1-4641-2473-0 (978-1-46412488-4 for the paperback version) distinguishes this book from all others. The last digit, 0, is there solely to detect errors that may occur when the ISBN is entered into a computer. Grocery items, credit cards, overnight mail, magazines, personal checks, travelers cheques, soft-drink cans, automobiles, and many other items that you encounter daily have identification numbers that code data, as well as a digit called a check digit for error detection. In this chapter, we examine some of the methods used to assign identification numbers and check digits.
Division by 9 Schemes
Let's begin by considering the U.S. Postal Service money order shown in Figure 16.1. The first 10 digits of the 11-digit number 17620289526 simply identify the money order. The last digit, 6, serves as an error-detecting mechanism. Let's see how this mechanism works. The 11th (last) digit of a Postal Service money order number is the remainder obtained when the sum of the first 10 digits of the number is divided by 9. In our example, the last digit is 6 because 1+7+6+2+0+2+0+2+8+9+5+2=42 and the remainder when 42 is divided by 9 is 6. (Recall that if we divide a positive integer a by a positive integer b, there are unique integers q and r such that a=bq+r, where r is nonnegative and less than b. The numbers q and r are called the quotient and remainder. For example, the remainder when 42 is divided by 9 is 6 because 42=9×4+6.)

Remainders

Now suppose that instead of the correct number, the number 17640289526 (an error in the fourth position) was entered into a computer that had been programmed for error detection in money orders. The machine would divide the sum of the first 10 digits of the entered number, 44, by 9 and obtain a remainder of 8. Because the last digit of the entered number is 6 rather than 8, the entered number cannot be correct. This crude method of error detection detects all errors involving a single digit except replacing a 0 with a 9, or vice versa. Because the value of a sum does not depend on the order in which the numbers are added, this method does not detect the transposition of digits such as 17260289526 instead of 17620289526. (The digits in positions 3 and 4 have been transposed.)
American Express travelers cheques, VISA travelers cheques, and Euro banknotes also use a check digit determined by division by 9. In these cases, the check digit is the smallest nonnegative integer such that the sum of the digits, including the check digit, is evenly divisible by 9.
EXAMPLE 1 The American Express Travelers Cheque
The American Express Travelers Cheque
The American Express Travelers Cheque with the identification number 387505055 has the check digit 7 because 3+8+7+5+0+5+0+5+5+=38 and 38+7 is evenly divisible by 9.
Self Check 1
If the sum of the digits of a Euro banknote serial number excluding the check digit is 68, what is the check digit?
- 4
Division by 7 Schemes
The scheme used on airline tickets and for Avis and National rental cars assigns the remainder after division by 7 of the number itself as the check digit, rather than dividing the sum of the digits by 7. For example, the check digit for the number 540047 is 4 because 540047 = 7 × 77149 + 4. This method will not detect the substitution of 0 for a 7, 1 for an 8, 2 for a 9, or vice versa. However, unlike the Postal Service method, it will detect transpositions of adjacent digits with the exceptions of the pairs that differ by 7, namely, 0, 7; 1, 8; and 2, 9. For example, if 5400474 were entered into a computer as 4500474 (the first two digits are transposed), the machine would determine that the check digit should be 3 because 450047 = 7 × 64292 + 3. Because the last digit of the entered number is not 3, the error has been detected.
One can use Google to determine easily the check digits that require division by 7 or 9. To find the Avis check digit for the number 540047, enter “540047 mod 7” in the Search box; for division by 9, enter the number followed by “mod 9.” To use a calculator to find the remainder when a is divided by b, first enter a÷b. The integer portion of the number is the quotient q. The remainder is r=a−bq. Doing this for 123÷7, we get 17.57, then 123−(7×17)=4. When a positive integer is divided by 10, the remainder is the first digit after the decimal point, but this is not true when dividing by other integers.
Universal Product Code
The scheme used on grocery products, the Universal Product Code (UPC), is more sophisticated. Consider the number 0 38000 00127 7 found on the bottom of a box of Kellogg's Corn Flakes. The first digit identifies a broad category of goods, the next five digits identify the manufacturer, the next five identify the product, and the last is a check digit. Suppose that this number were entered into a computer as 0 58000 00127 7 (a mistake in the second position). How would the computer recognize the mistake?
For any UPC number a1a2a3a4a5a6a7a8a9a10a11a12, the computer is programmed to carry out the following computation:
3a1+a2+3a3+a4+3a5+a6+3a7+a8+3a9+a10+3a11+a12
If the result doesn't end with a 0, the computer knows the entered number is incorrect.
For the incorrect corn flakes number, we have
3 ⋅ 0 + 5 + 3 ⋅ 8 + 0 + 3 ⋅ 0 + 0 + 3 ⋅ 0 + 0 + 3 ⋅ 1 + 2 + 3 ⋅ 7 + 7 = 62
Because 62 doesn't end with 0, the error is detected. Notice that had we used the correct digit 3 in the second position instead of 5, the sum would have ended in a 0 as it should. This simple scheme detects all single-position errors and about 89% of all other kinds of errors.
Beginning in January 2005, U.S. retailers were required to have software that could read the 12-digit UPC code used in the United States and the 13-digit European Article Number (EAN) code used in Europe. This change paves the way for the 13-digit EAN to become the worldwide standard. Existing UPC numbers will be converted to EAN numbers by adding an extra 0 at the beginning. The check digit for a 13-digit EAN number a1a2a3a4a5a6a7a8a9a10a11a12a13 is selected so that
a1+3a2+a3+3a4+a5+3a6+a7+3a8+a9+3a10+a11+3a12+a13
ends with 0. Adding an extra 0 in the front of a UPC number does not affect the check digit. The coefficient 3 for the terms with even subscripts is called a weight. Because 1ai=ai , we say that the terms with odd subscripts have weight 1.
Besides error detection, check-digit schemes that use weighted sums can be used to find a digit that has been corrupted in some way. Say, for example, that the packaging for a product with UPC number 1 640002 202034 was damaged or defective in such a way that the second digit was unintelligible. How would we know that it is supposed to be 6? Well, let's call it x. Then we know that the weighted sum
1+3⋅x+4+3⋅0+2+3⋅0+2+3⋅2+0+3⋅2+0+3⋅3+4=3x+32
must end with 0. Because 6 is the only digit that makes this true, we know the corrupted digit is 6. This example also illustrates why the weight 3 is superior to the weight 2. While there is only one digit that makes the expression 3x+32 end with 0, there are two digits that make 2x+32 end with 0: x=4 and x=9.
Bank Identification Numbers
The U.S. banking system uses a variation of the UPC scheme that appends check digits to the numbers assigned to banks. Each bank has an eight-digit routing number a1a2 ⋯ a8 together with a check digit a9 so that a9 is the last digit of
7a1+3a2+9a3+7a4+7a5+9a6+7a7+3a8
In this formula, the weights are 7, 3, and 9. The weights were carefully chosen so that all single-digit errors and most transposition errors are detected.
EXAMPLE 2 Bank Routing Number
Bank Routing Number
The check illustrated in Figure 16.2 has routing number 062000019. The check digit 9 is the last digit of
7⋅0+3⋅6+9⋅2+7⋅0+3⋅0+9⋅0+7⋅0+3⋅1=39
The first four digits of a nine-digit bank routing number identify the bank's Federal Reserve District, office, state, or special collection arrangement; the next four digits are the bank's identification number; the ninth digit is the check digit. The block of numbers 33 74489 shown in Figure 16.2 is the account number. The last block, 0134, is the check number.

You may wonder if there is any advantage to using three weights for the routing number as opposed to using two, as is the case for the UPC error-detection scheme. The answer is yes. While both the UPC scheme and the bank scheme detect 100% of single-position errors and most transposition errors involving adjacent digits, the bank scheme will detect most transposition errors of the form ⋯abc⋯→⋯cba⋯, whereas the UPC scheme does not detect such errors.
For example, say that we look at a number that begins with 241. In the UPC scheme, these digits contribute 3⋅2+4+3⋅1=13 toward the total calculation, while the string 142 (the first and third digits are transposed) also contributes 3⋅1+4+3⋅2=13 toward the total calculation. So the error is not detected. In contrast, using the bank scheme, 241 contributes 7⋅2+3⋅4+9⋅1=35 toward the total, while 142 contributes 7⋅1+3⋅4+9⋅2=37 toward the total. Because the total for the correct number ends with 0, the total for the number that had the transposition error would end with the digit 2. Thus, the error is detected.
Self Check 2
If a number of the form 71a3a4⋯a9 is a valid bank routing number, is 71a3a4⋯a9 a valid bank routing number?
- No. Since 71 contributes 2 to the last digit of the weighted sum of the digits of 71a3a4⋯a8 and 17 contributes 8 to the last digit of weighted sum of the digits of 17a3a4⋯a8, a9 is not the last digit of the weighted sum of the digits 17a2a3⋯a8.
Luhn Algorithm
One of the most efficient error-detection methods is the Luhn algorithm, created in 1953 by the IBM scientist Hans Peter Luhn, used by all major credit-card companies, as well as by many libraries, blood banks, and the South Dakota driver's license department. For a credit card number a1a2a3a4a5a6a7a8a9a10a11a12a13a14a15, let T be the number of digits in positions 1, 3, 5, 7, 9, 11, 13, 15 that are 5 or greater. The check digit a16 is chosen so that 2a1+a2+2a3+a4+2a5+a6
+2a7+a8+2a9+a10+2a11+a12+2a13+a14+2a15+T+a16 is divisible by 10.
EXAMPLE 3 Luhn Algorithm Check Digit
Luhn Algorithm Check Digit
To demonstrate how to calculate a check digit using the Luhn algorithm, suppose a bank intends to issue a credit card with the identification number 312560019643001. We calculate 2⋅3+1+2⋅2+5+2⋅6+0+2⋅0+1+2⋅9+6+2⋅4+3+2⋅0 +0+2⋅1 to get 66. Then we note that among the digits in the odd-numbered positions, only 6 and 9 are greater than or equal to 5. So we add 2 to 66 to get 68. The check digit is whatever is needed to bring the final tally to a number that ends with 0. Because 68+2=70, the check digit for our example is 2. This digit is appended to the end of the number the bank issues for identification purposes. Errors in input data are detected by applying the same algorithm to the input, including the check digit. If the correct number is entered into a computer, the result will end in 0. If the result doesn't end with 0, a mistake has been detected.
The credit card illustrated in Figure 16.3 has a check digit that is not valid because the algorithm yields
2⋅4+1+2⋅2+8+2⋅0+0+2⋅1+2+2⋅3+4+2⋅5+6+2⋅7+8+2⋅9+3+0=94
which does not end in 0. This method allows computers to detect 100% of singleposition errors and about 98% of other common errors. For credit cards such as American Express that use 14 digits plus a check digit, the weights are 1,2,1,2,…,1,2 instead of 2,1,2,1,…,2,1.

Besides detecting errors, a check digit offers partial protection against fraudulent numbers. A person who wanted to create a phony credit card, bank account number, or driver's license number would have to know the appropriate check-digit scheme for the number to go unchallenged by the computer.
Self Check 3
If the first three digits of a 16-digit credit card are 924, what do they contribute to the weighted sum total when calculating the check digit?
- 29
International Standard Book Numbers
Thus far, we have not discussed any schemes that detect 100% of single errors and 100% of transposition errors. As seen on the back of this book and most others published since 2007, there are two identification numbers—a 13-digit number called the 13-digit International Standard Book Number (ISBN-13) and a 10-digit number, called the 10-digit ISBN (ISBN-10). The 10-digit ISBN detects 100% of single-digit errors and 100% of transposition errors.
A correctly coded 10-digit ISBN a1a2⋯a10 has the property that 10a1+9a2+8a3+7a4+6a5+5a6+4a7+3a8+2a9+a10 is evenly divisible by 11. Consider the 10-digit ISBN of the book that you are now reading: 1-4641-2473-6 (1-46412488-4 for paperback version). The 1 at the beginning indicates that the book is published in an English-speaking country, while the next block of digits, 4641, identifies the publisher, W. H. Freeman and Company. The third block for the hardback edition, 2473, is assigned by the publisher and identifies this particular book. The last digit 6, for the hardback version, is the check digit. Let's verify that this number is a legitimate possibility. We must compute 10⋅1+9⋅4+8⋅6+7⋅4+6⋅1+5⋅2+4⋅4+3⋅7+2⋅3+6=187. Because 187=11⋅17, it is evenly divisible by 11, so no error has been detected.
Self Check 4
If the weighted sum of the digits of an ISBN excluding the check digit is 87, what is the check digit?
- 1
How can we be sure that this method detects 100% of the single-position errors? Let's say that a correct number is a1a2a3a4a5a6a7a8a9a10 and that a mistake is made in the second position. (The same argument applies equally well in every position.) We may write this incorrect number as a1a′2a3a4a5a6a7a8a9a10, where a′2≠a2. For this error to go undetected, it must be the case that 10⋅a1+9⋅a′2+8⋅a3+7⋅a4+6⋅a5+5⋅a6+4⋅a7+3⋅a8+2⋅a9+a10 is evenly divisible by 11. Then, because both 10a1+9a2+8a3+7a4+6a5+5a6+4a7+3a8+2a9+a10 and 10a1+9a′2+8a3+7a4+6a5+5a6+4a7+3a8+2a9+a10 are divisible by 11, so is their difference:
(10⋅a1+9⋅a2+8⋅a3+⋯+a10)−(10⋅a1+9⋅a′2+8⋅a3+⋯+a10)=9⋅(a2−a′2)
Because a2 and a′2 are distinct digits between 0 and 9, their difference must be one of ±1,…,±9. Thus, the only possibilities for the number 9⋅(a2−a′2) are ±9,±18±27,±36,±45,±54,±63,±72,±81—and none of these is divisible by 11. So a single-position error cannot go undetected.
EXAMPLE 4 ISBN-10 Single-Error Detection
ISBN-10 Single-Error Detection
To illustrate with a specific example why the ISBN-10 method detects single errors, let's say the valid ISBN 1-4292-0900-3 is mistaken as 1-2292-0900-3 (an error in position 2). Because the correct second digit in the weighted sum contributes 9⋅4=36 to the total of 176 and the incorrect second digit contributes 9⋅2=18, we see that the weighted sum of the incorrect number is 176−18=158. But 158 is not evenly divisible by 11, so the error is detected.
To verify that the ISBN-10 method detects all adjacent transposition errors, let's suppose that the first two digits are transposed. (The same argument applies to all positions.) Say that the correct number is a1a2a3⋯a10. As before, for the incorrect number a1a2a3⋯a10 to go undetected, it must be the case that the difference of the correct number and the incorrect number is evenly divisible by 11. That is,
(10a1+9a2+8a3+⋯+a10)−(10a2+9a1+8a3+⋯+a10)
is evenly divisible by 11. This reduces to the condition that a1−a2 is divisible by 11. But the only possible differences of two numbers between 0 and 9 are plus or minus the numbers between 0 and 9, and of these only 0 is divisible by 11. Thus, a1−a2=0. But then a1=a2 and there is no error.
EXAMPLE 5 ISBN-10 Transposition-Error Detection
ISBN-10 Transposition-Error Detection
Let's trace through an example to see how the ISBN-10 method detects adjacent transposition errors. Say 1-4292-0900-3 is mistaken as 1-2492-0900-3 (digits in positions 2 and 3 are transposed). Because the second and third digits in the weighted sum of the correct number contribute 9⋅4+8⋅2=52 to the total of 176 and the second and third digits of the incorrect number contribute 9⋅2+8⋅4=50 to the weighted sum, we know that the weighted sum of the incorrect number is 176−2=174, which is not evenly divisible by 11.
With a bit more work, we could prove that every transposition error is detected, not just the transpositions of adjacent digits. This is possible because 11 is prime.
Because the ISBN-10 method, in contrast to the other methods we have described, detects all single-position errors and all transposition errors, why is it not used more? Well, it does have a drawback. Say the next title published by W. H. Freeman is to have 0902 for the third block. (The 10-digit ISBN for all W. H. Freeman books begins with 1-4641.) What check digit should be assigned? Call it a. Then the weighted sum is 10⋅1+9⋅4+8⋅6+7⋅4+6⋅1+5⋅4+4⋅5+3⋅1+2⋅3+a=177+a. Because the next integer after 177 that is divisible by 11 is 187, we see that a=10. But appending 10 to the existing 9-digit number would result in an 11-digit number instead of a 10-digit one. This is the only flaw in the 10-digit ISBN scheme. To avoid this flaw, publishers use an X to represent the check digit 10. As a result, not all 10-digit ISBNs consist solely of digits; some end with X. Publishers could avoid this inconsistency by simply refraining from using numbers that require an X.
To expand the inventory of ISBNs and make them compatible with the UPC/EAN numbering scheme for other retail items worldwide, publishers began using a 13-digit ISBN in 2007. The 13-digit ISBN is the same as the 10-digit ISBN number except for a prefix of 978 or 979 and the check digit. The check digit for the 13-digit ISBN is calculated so that the weighted sum using the weights 1,3,1,3,…,1,3,1 ends with 0. Thus, the 13-digit ISBN and the 13-digit UPC/EAN numbers used for retail products employ the same check-digit method. During a phase-in period, publishers will use both the 10-digit and 13-digit numbers.
Although all the check-digit schemes that we have described in this chapter that use weighted sums detect 100% of single-digit errors, it is impossible to devise a check-digit scheme that employs a single check digit that detects 100% of multiple-digit errors. In the case of the UPC scheme, for instance, while one error might cause the weighted sum to be, say, 62 (and thereby detect the error), a second error may result in the sum 70 so that no errors are detected. Consider the single-digit error that we examined earlier for corn flakes. Recall the correct UPC number is 0 38000 00127 7 and its weighted sum is 60. For the incorrect corn flakes number 0 58000 00127 7 (with a single error in position 2), we have
3⋅0+5+3⋅8+0+3⋅0+0+3⋅0+0+3⋅1+2+3⋅7+7=62
But if we also make a second error of using 8 in position 4 instead of 0, so that the number becomes 0 58800 00127 7, the errors are not detected because its weighted sum is 70, which does end with 0. Nevertheless, the weight schemes detect most multiple errors because it is rare when a second or third error exactly cancels out previous errors.
A Multiplication by 13 Scheme
After single-digit errors and adjacent transposition errors, the third most common error is one of the form ⋯abc⋯→⋯cba⋯. In practice, these kinds of errors commonly occur in phone numbers that have matching digits separated by another digit such as 727 5856. A likely mistake when writing or dialing this number is to switch the 8 and the 6, resulting in the number 727 5658. Such an error is called a jump transposition. Remarkably, there is a simple way to encode identification numbers so that the three most common errors are detected 100% of the time without having to introduce an alphabetic character, as is done for the 10-digit ISBN numbers.
To illustrate the method, suppose that a math instructor wants to post student grades publicly without revealing any information about the students' ID numbers. Assuming the last four digits of each student ID number are different, she could assign each student a six-digit number by multiplying the last four digits of their identification numbers by 13 (adding leading 0s when necessary). For example, a student with an ID number that ends with 8912 is assigned 115856=8912×13. (To preserve confidentiality of the original four digits, students are not informed of the encoding method.) Of course, the instructor can recapture the original fourdigit numbers by dividing the encoded numbers by 13. Since all encoded numbers are divisible by 13, the jump transposition error 115856→115658 is detected because 115658 is not divisible by 13.
The arguments for verifying that encoding identification numbers as multiples of 13 detect 100% of all single-digit errors, all transposition errors involving adjacent digits, and all jump transposition errors are similar to those we used to show that the 10-digit ISBN numbers detect errors. In particular, a single-digit error in the number anan−1⋯ai⋯a0 of the form anan−1⋯a′i⋯a0, where a′i≠ai. is not detected if and only if anan−1⋯a′i⋯a0 is a multiple of 13. But if both anan−1⋯ai⋯a0 and anan−1⋯a′i⋯a0 are multiples of 13, then so is their difference (anan−1⋯a′i⋯a0)−(anan−1⋯a′i⋯a0)=(ai−a′i)10i. But 13 does not divide the term on the right when ai≠a′i. Similarly, the transposition of adjacent digits ai and ai−1 is undetected if and only if 9(ai−ai−1)10i−1 is divisible by 13, which happens only when ai=ai−1. And the jump transposition ⋯aiai−1ai−2⋯→⋯ai−2ai−1ai⋯ is undetected if and only if 99(ai−ai−2)10i−2 is divisible by 13, which happens only when ai=ai−2. Incidentally, the arguments just given reveal why we used multiplication by 13 rather than some smaller positive integer. For example, if multiplication by 11 were used to transform the identification numbers instead of 13, then all single-digit errors and all adjacent transposition errors are detected, but not all jump transpositions are, because 11 divides 99.
Euro banknotes, car rental companies, some state driver's license numbers, and the vehicle identification number (VIN) that identifies cars and trucks use alpha-numeric identification numbers. To calculate the check digit, the letters are assigned numerical values. See Spotlight 16.1.
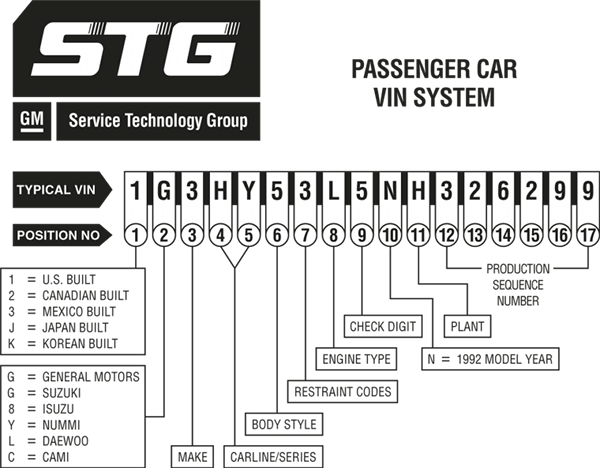
The VIN System 16.1
16.1
Automobiles and trucks are given a VIN by the manufacturer. A typical VIN has 17 alphanumeric characters that code information such as the country where the vehicle was built, manufacturer, make, body style, engine type, plant where the vehicle was built, model year, model, type of restraint, a check digit, and a production sequence number. The check digit is calculated by converting the 26 consecutive letters of the alphabet to the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 2, 3, 4, 5, 6, 7, 8, 9 (note the skipped digit after the second 9) to obtain a 16-digit number a1a2⋯a15a16 that is weighted with 8, 7, 6, 5, 4, 3, 2, 10, 9, 8, 7, 6, 5, 4, 3, 2. The check digit is the remainder when the weighted sum 8⋅a1+7⋅a2+⋯+3⋅a15+2⋅a16 is divided by 11 unless the remainder is 10, in which case an X is used instead. The check digit is inserted in position 9.
Summary of Error Detection Schemes
Postal money orders The last digit of a Postal Service money order number is the remainder obtained when the sum of the first 10 digits of the number is divided by 9. This method will detect any single mistake except replacing 0 with a 9 or vice versa.
American Express and VISA travelers cheques; Euro banknotes The last digit is the smallest nonnegative integer such that the sum of the digits, including the check digit, is divisible by 9. This method will detect any single mistake except replacing 0 with a 9 or vice versa.
Airlines; Avis and National rental cars The last digit is the remainder after division by 7 of the number itself, excluding the last digit. This method will detect any single error except the substitution of 0 for a 7, 1 for an 8, 2 for a 9, or vice versa. It will detect transpositions of adjacent digits with the exceptions of the pairs 0, 7; 1, 8; and 2, 9.
UPCs For any UPC number a1a2a3a4a5a6a7a8a9a10a11a12, the last digit is chosen so that 3a1+a2+3a3+a4+3a5+a6+3a7+a8+3a9+a10+3a11+a12 is divisible by 10. This method detects 100% of all single errors and 89% of most others.
EANs For any EAN a1a2a3a4a5a6a7a8a9a10a11a12a13, the last digit is chosen so that a1+3a2+a3+3a4+a5+3a6+a7+3a8+a9+3a10+a11+3a12+a13, is evenly divisible by 10. This method detects 100% of all single-digit errors and 89% of most others.
Bank routing numbers For a bank routing number a1a2a3a4a5a6a7a8, the check digit a9 is the last digit of 7a1+3a2+9a3+7a4+3a5+9a6+7a7+3a8. This method detects 100% of all single errors and 89% of most others.
Luhn algorithm For a credit card number a1a2a3a4a5a6a7a8a9a10a11a12a13a14a15, let T be the number of digits in positions 1, 3, 5, 7, 9, 11, 13, 15 that are greater than or equal to 5. The last digit a16 is chosen so that 2a1+a2+2a3+a4+2a5+a6+2a7+a8+2a9+a10+2a11+a12+2a13+a14 +2a15+T+a16 is divisible by 10. This method detects 100% of all single errors; all transposition errors involving adjacent digits except for the pair 0, 9; and 98% of most other errors.
ISBN-10s A correctly coded 10-digit ISBN a1a2⋯a10 has the property that 10a1+9a2+8a3+7a4+6a5+5a6+4a7+3a8+2a9+a10 is evenly divisible by 11. This method detects 100% of all single errors and 100% of all transposition errors. If a10 is X, it is replaced with 10 in the weighted sum.
ISBN-13s This scheme is the same as the UPC scheme.
Multiplication by 13 This method detects all single-digit errors, all transposition errors involving adjacent digits, and all jump transposition errors.