16 Identification Numbers

Chapter 16 Exercises

16.1 Check Digits

Question 16.31

1. Determine the check digit for a money order with identification number 3953981640.

Question 16.32

2. Determine the value of ? so that 7?345417803 is a valid money order identification number.

Question 16.33

3. Determine the check digit for the Avis identification number 873345672.

Question 16.34

4. Determine two values for ? that will make 723459?0161 a valid Postal Service money order number.

Question 16.35

5. Determine the check digit for the airline ticket number 30860422052.

Question 16.36

6. Suppose a money order with the identification number and check digit 21720421168 is erroneously copied as 27750421168. Will the error be detected? Explain your reasoning.

Question 16.37

7. Determine the check digit for the travelers cheque with identification number 661340874.

Question 16.38

8. Determine the check digit for an Avis rental car with identification number 651421.

Question 16.39

9. If a Postal Service money order with identification number $19 a_{3} a_{4} \dots a_{10}$ has the check digit 5, what is the check digit for the Postal Service money order number $33 a_{3} a_{4} \dots a_{10}$ ?

Question 16.40

10. Which of the error detection schemes below will detect some errors of the form $a b c \to c b a$ (jump transposition)?

UPC code
Bank scheme
13-digit ISBN

Question 16.41

11. If an Avis identification number $a_{1} a_{2} \dots a_{10} a_{11} 8$ has the check digit 5, what is the check digit for the Avis identification number $a_{1} a_{2} \dots a_{10} a_{11} 6$ ?

11.

Question 16.42

12. Find the check digit for the UPC number 03608072089.

Question 16.43

13. Suppose that the packaging of a retail item were damaged in such a way that the first digit of a 12-digit UPC code was scratched off, but the remaining 11 digits were 88072303584; determine the first digit.

13.

Question 16.44

14. The fourth digit of the UPC number shown below is not discernible. Determine the correct value.

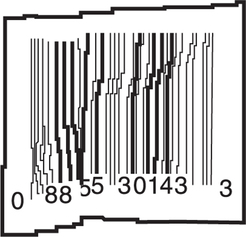
Question 16.45

15. If one randomly chooses a large number of 10-digit ISBNs, about what percent would have an $X$ in the check digit position?

15.

10%

Question 16.46

16. Determine the ISBN-10 check digit for the number 0-547-16509.

Question 16.47

17. Determine the ISBN-13 check digit for the number 978-0-547-16509.

17.

Question 16.48

18. When the eighth edition of this textbook was in preparation, the publisher sent the author of this section the following ISBNs for the book: ISBN-10: 1- 4292-0900-3; ISBN-13: 978-1-4292-0890-0. How did the author know the ISBN-13 was wrong, and how did he know how to correct it? (This really happened!)

Question 16.49

19. When calculating the check digit for a 13-digit ISBN, why can you disregard the first two digits? (Try it for Exercise 16.)

19.

The lead digits 97 contribute 30 to the weighted sum. Thus, the digit needed to make the sum evenly divisible by 10 is the same if you leave the 9 and 7 out of the calculation. (For example, if the sum were 162, including the 97 digits, then the sum would be 132 if it didn’t include them. In either case, the check digit is 8.)

Page 694

Question 16.50

20. Determine the check digit for the bank routing number 09100001.

Question 16.51

21. Determine the check digit for an American Express Travelers Cheque with identification number 461212023.

21.

Question 16.52

22. Suppose that a check digit is assigned to a four-digit number by appending the remainder after division by 7. If the number 36806 has a single-digit error in the first position, determine the possibilities for the correct number.

Question 16.53

23. Determine whether the MasterCard number 3541 0232 0033 2270 is valid.

23.

Yes, it is valid.

Question 16.54

24. Suppose that the digit indicated by a question mark in the MasterCard number 426452002177?337 is unreadable. What is the unreadable digit?

Question 16.55

25. Suppose that a valid credit card number of the form $11 a_{3} a_{4} \dots a_{16}$ is changed to $55 a_{3} a_{4} \dots a_{16}$ . Is the result a valid credit number?

25.

No. Because 11 contributes 3 to the running total, whereas 55 contributes 16, the running total for the changed number will end with 3 instead of 0.

Question 16.56

26. Suppose that a valid credit card number of the form $22 a_{3} a_{4} \dots a_{16}$ is changed to $55 a_{3} a_{4} \dots a_{16}$ . Is the result a valid credit number?

Question 16.57

27. Suppose a correctly coded credit card number $a_{1} a_{2} \dots a_{16}$ is modified in such a way that the sum produced by the Luhn algorithm is increased by 10. Explain why the credit card error detection method does not detect the error. What happens if the sum is increased by 12?

27.

The Luhn algorithm for a valid credit card results in a running total that ends with 0, so increasing the sum by 10 would still give a total that ends with 0. Thus, the new number is valid. Increasing the sum by 12 changes the last digit of the running total to 2, which is not a valid credit number.

Question 16.58

28. If a number of the form $a_{1} a_{2} \dots a_{13} a_{14} 34$ is a valid credit card number, what is the check digit for a credit number of the form $a_{1} a_{2} \dots a_{13} a_{14} 5$ ?

Question 16.59

29. If a credit card number of the form $83 a_{3} \dots a_{15} 4$ is valid credit card number, what is the check digit for a credit number of the form $19 a_{3} \dots a_{15}$ ?

29.

Question 16.60

30. Replace the question mark in the number JM1GD222?J1581570 with a digit that will result in a valid VIN. (See Spotlight 16.1 on page 678 for a description of the method to be used.)

Question 16.61

31. Create a check digit for the UPC number 38137009213 using the weights 7, 1, 7, 1, 7, 1, …, 7, 1, instead of 3, 1, 3, 1, 3, 1, …, 3, 1. Test to see whether this check digit will detect single-digit errors by trying several examples.

31.

The check digit is 7. This check digit method detects all single-digit errors.

Question 16.62

32. Create a check digit for the UPC number 38137009213 using the weights 2, 1, 2, 1, 2, 1, …, 2, 1, instead of 3, 1, 3, 1, 3, 1, …, 3, 1. Is the error caused by replacing the 3 in the first position with an 8 detected? What about the error caused by replacing the 1 in the third position with a 6? Explain why or why not.

Question 16.63

33. If the weights 5, 1, 5, 1, 5, 1, …, 5, 1 were used for the UPC code, which single-digit errors would go undetected?

33.

In the odd-numbered positions, an error caused by replacing an odd digit by an odd digit or an even digit replaced by an even digit is not detected.

Question 16.64

34. Exercises 31-33 reveal that using the weights 1, 3, or 7 for a particular position detects all errors in that position, whereas using weights 2 or 5 in a position does not detect all errors. Using this observation, make a guess about error-detection capability using weights 9, 4, 6, or 8.

Question 16.65

35. Enter the number 036000260809 in a Google search box. Is it a valid UPC number? Now change any one digit. Is the new number a valid UPC number? Try a different change.

35.

It is the UPC code for Kleenex. Changing exactly one digit will not result in a valid UPC number.

Question 16.66

36. Suppose that a valid credit card number $90 a_{3} a_{4} \dots a_{16}$ is mistakenly entered into a credit card reader as $90 a_{3} a_{4} \dots a_{16}$ . Explain why the Luhn algorithm does not detect the error.

Question 16.67

37. If a valid credit card number using the Luhn algorithm has the form $47 a_{3} \dots a_{15} a_{16}$ , determine the check digit of the number if the first two digits were transposed and the digits in positions 3 through 15 were unchanged.

37.

The new check digit is $x - 4$ or $x + 6$ , depending on whether $x$ is greater than or equal to 4 or less than 4.

Question 16.68

38. If a credit card number of the form $83 a_{3} \dots a_{15} a_{16}$ is a valid credit card number, what is the check digit for a credit card number of the form $18 a_{3} \dots a_{15} a_{16}$ ?

Question 16.69

39. Explain why encoding ID numbers by multiplying them by 15 would not detect the single-digit error of replacing 114180 by 114150.

39.

Because the difference, $114180 − 114150 = 30$ , is a multiple of 15.

Question 16.70

40. Explain why encoding ID numbers by multiplying them by 15 would not detect the transposition error of replacing 125025 by 120525.

Question 16.71

41. Explain why encoding ID numbers by multiplying them by 17 would detect all single-digit errors, adjacent transposition errors, and jump transposition errors.

41.

The same arguments in the text for multiplying by 13 apply when multiplying by 17.

Question 16.72

42. State a general criterion for the detection of an error of the form $\dots a b c \dots \to \dots c b a \dots$ for the routing number of a checking account.

Question 16.73

43. The 10-digit ISBN 0-669-03925-4 is the result of a transposition of two adjacent digits not involving the first or last digit. Determine the correct ISBN.

43.

0-669-09325-4

Question 16.74

44. Explain why the bank scheme will detect the error $751 \dots \to 157 \dots$ but the UPC scheme will not.

Page 695

Question 16.75

45. Suppose that the check digit $a_{9}$ for the bank routing number was chosen to be the last digit of $3 a_{1} + 7 a_{2} + a_{3} + 3 a_{4} + 7 a_{5} + a_{6} + 3 a_{7} + 7 a_{8}$ instead of using the method described in this chapter. How would this compare with the actual check digit?

45.

If $c_{1}$ is the check digit for the weights 7, 3, 9, 7, 3, 9, 7, 3 and $c_{2}$ is the check digit for the weights 3, 7, 1, 3, 7, 1, 3, 7, then $c_{2} = 0$ when $c_{1} = 0$ . Otherwise, $c_{2} = 10 - c_{1}$ .

Question 16.76

46. Explain why an error caused by transposing the first two digits of a Postal Service money order is not detected by the check-digit scheme. Explain why the same is true for the second and third digits. What about the last two digits?

Question 16.77

47. Suppose that a company assigns an extra digit to every employee Social Security number by appending a 0 if the sum of the digits is even and a 1 if the sum is odd. If a 2 were mistakenly read as a 7, would the error be detected? What if a 2 were mistakenly read as an 8? Try a few other experiments with single-digit errors. (For experiments, you can use three-digit numbers instead of nine-digit numbers.) Determine which errors are detected by this method. Explain your reasoning. Approximately what percentage of errors is detected by appending the extra digit?

47.

The mistake of reading a 2 as a 7 is detected because the sum of the digits of the incorrect number would be odd. The mistake of reading a 2 as an 8 is not detected because the sum of the digits of the incorrect number would remain even. An error is detected when an odd digit is misread as an even one (or vice versa) because the sum of the digits changes from even to odd (or vice versa). Approximately 50% of errors are detected.

Question 16.78

48. Explain why the Postal Service money order check-digit scheme does not detect the mistake of substituting a 0 for a 9, or vice versa.

Question 16.79

49. Which digit never appears as a check digit on a Postal Service money order?

49.

Because the remainder upon dividing by 9 is less than 9, 9 cannot be a remainder.

Question 16.80

50. Which digit never appears as a check digit on an American Express Travelers Cheque?

Question 16.81

51. Which digits never appear as a check digit for an airline identification number?

51.

Because the remainder after dividing by 7 is less than 7, the digits 7, 8, and 9 cannot be a check digit.

Question 16.82

52. Suppose that four-digit numbers $a_{1} a_{2} a_{3} a_{4}$ are assigned a check digit $a_{5}$ so that $a_{1} + 2 a_{2} + a_{3} + 2 a_{4} + a_{5}$ is evenly divisible by 10. Test the number 43216 created in this way to see whether the method detects adjacent transposition errors.

Question 16.83

53. Starting with the 10-digit ISBN 0-7167-4782-0, create three new numbers by transposing any two different digits. (They need not be adjacent.) Are these errors detected by the scheme?

53.

Yes. The ISBN-10 scheme detects all transposition errors.

Question 16.84

54. Suppose that in an Avis identification number, an 8 is mistaken for a 5. Is the error detected? What if a 9 is mistaken for a 2?

Question 16.85

55. Give an argument to show that the 10-digit ISBN error-detection method will detect a digits. Does the same argument work for the fourth transposition error involving the first and third and sixth digits?

55.

For the transposition to go undetected, it must be the case that the difference of the correct number and the incorrect number is evenly divisible by 11. That is, $(10 a_{1} + 9 a_{2} + 8 a_{3} + ... + a_{10}) - (10 a_{3} + 9 a_{2} + 8 a_{1} + ... + a_{10})$ is divisible by 11. This reduces to $2 a_{1} - 2 a_{3} = 2 (a_{1} - a_{3})$ is divisible by 11. But $2 (a_{1} - a_{3})$ is divisible by 11 only when $a_{1} - a_{3}$ is divisible by 11 and this happens only when $a_{1} - a_{3} = 0$ . In this case, there is no error. The same argument works for the fourth and sixth digits.

Question 16.86

56. Suppose the check digit $a_{10}$ of 10-digit ISBNs were chosen so that $a_{1} + 2 a_{2} + 3 a_{3} + 4 a_{4} + 5 a_{5} + 6 a_{6} + 7 a_{7} + 8 a_{8} + 9 a_{9} + 10 a_{10}$ is divisible by 11 instead of using the method described in the chapter. How would this compare with the actual check digit?

Question 16.87

57. Consider a UPC number in which the digits 7 and 2 appear consecutively (i.e., the number has the form $\dots 72 \dots$ ). Will the error caused by transposing these digits (i.e., the number is taken as $\dots 27 \dots$ ) be detected? What if the digits 6 and 2 were transposed instead? State the general criterion for the detection of an error of the form $\dots ab \dots \to \dots ba \dots$ by the UPC scheme.

57.

The combination 72 contributes $3 \cdot 2 + 7 = 23$ or $7 + 3 \cdot 2 = 13$ (depending on the location of the combination) toward the total sum, while the combination 27 contributes $3 \cdot 2 + 7 = 13$ or $2 + 7 \cdot 3 = 23$ . So, the total sum resulting from the number with the transposition is still divisible by 10. Therefore, the error is not detected. Similarly, the combination 26 contributes $3 \cdot 2 + 6 = 12$ toward the total sum, whereas the combination 62 contributes $3 \cdot 6 + 2 = 20$ toward the total sum; so the new sum will not be divisible by 10. Similarly, when the combination 26 contributes $2 + 3 \cdot 6 = 20$ to the total, the combination 62 contributes $6 + 3 \cdot 2 = 12$ to the total. So, the total for the number resulting from the transposition will not be divisible by 10 and the error is detected. In general, an error that occurs by transposing $a b$ to $b a$ is undetected if and only if

$a - b$ is 5 or −5.

Question 16.88

58. If the first three digits of a routing number for a checking account are 537 and the 5 and 3 are transposed, will the error be detected? If the first three numbers are 237 and the 2 and 7 are transposed, will the error be detected?

Question 16.89

59. The Canadian province of Quebec assigns a check digit $a_{12}$ to an 11-digit driver’s license number $a_{1} a_{2} \dots a_{11}$ so that $12 a_{1} + 11 a_{2} + 10 a_{3} + 9 a_{4} + 8 a_{5} + 7 a_{6} + 6 a_{7} + 5 a_{8} + 4 a_{9} + 3 a_{10} + 2 a_{11} + a_{12}$ is divisible by 10. Criticize this method. Describe all single-digit errors that are undetected by this scheme.

59.

Many single-digit errors go undetected. Substitution of $b$ for $a$ where $a$ is 5 or −5 in positions 1, 5, 7, 9, and 11 is undetected; all errors in position 3 are undetected; substitution of $b$ for $a$ where $b - a$ is even in position 8 is undetected.

Question 16.90

60. Speculate on the reason why telephone numbers, Social Security numbers, and serial numbers on most currency do not have check digits.

Question 16.91

61. Suppose that a company uses a check-digit scheme similar to the UPC scheme, except that instead of using the UPC weights 3, 1, 3, 1, …, it uses $w$ , 1, $w$ , 1, …. If two of the ID numbers used by the company are 73215674 and 73215661, determine $w$ .

61.

Because both numbers are valid, the difference of the weighted sums is divisible by 10. That is, $(7 w + 3 + 2 w + 1 + 5 w + 6 + 7 w + 4) - (7 w + 3 + 2 w + 1 + 5 w + 6 + 6 w + 1)$ is divisible by 10. The difference simplifies to $w + 3$ . So, $w = 7$ .

Question 16.92

62. If a publishing company has headquarters in both the United States and Germany and publishes the same book in both countries, it is likely that the 10-digit ISBN for the book will be identical except for the first and last digits (because the first digit for U.S. publications is 0 and the first digit for German publications is 3). If the last digit of the U.S. edition is 1, what is the last digit for the German publication?

16.2 The ZIP Code

16.3 Bar Codes

Question 16.93

63. Determine the ZIP + 4 code and check digit for each of the following Postnet bar codes.

63.

(a) 51593-2067; 2

(b) 50347-0055; 1

Page 696

Question 16.94

64. In each of the following Postnet bar codes, exactly one mistake occurs (i.e., a long bar appears instead of a short one, or vice versa). Determine the correct ZIP code.

Question 16.95

65. Below is a 12-digit delivery-point bar code. Determine the ZIP + 4 number, the last two digits of the street address, and the check digit.

65.

55811-2742; 22; 1

Question 16.96

66. If the check digit for the ZIP + 4 code for a house on 1738 Maple Street is 3, what would the check digit for the delivery-point code be?

Question 16.97

67. Find the check digit for the ZIP + 4 code 50037-2452.

67.

Question 16.98

68. Explain why any two errors in a particular block of five bars in a Postnet code are always detectable. Explain why not all such errors can be corrected.

Question 16.99

69. Form all possible strings consisting of exactly three $a$ ’s and two $b$ ’s and arrange the strings in alphabetical order. (For example, the first two possibilities are aaabb and aabab.) Do you see any relationship between your list and the Postnet code?

69.

If you replace each short bar in the bar code table by an $a$ and replace each long bar in the bar code table by a $b$ , the resulting strings are listed in alphabetical order.

Question 16.100

70. The back cover of recently published books includes a bar code that has the 10-digit ISBN above the bars and a 13-digit identification number below the bars (see below). Examine the bar code on several books. How does the number below the bar code differ from the UPC code?

Question 16.101

71. Suppose that the first block of a UPC bar code following the guard bar pattern that a scanner reads is 1000100. Is the scanner reading left to right or right to left?

71.

Right to left

16.4 Encoding Personal Data

Question 16.102

72. If a Social Security number begins with 0, the number was issued in a state in the

Northeast.
Midwest.
West.

Question 16.103

73. The Canadian postal system has assigned each geographic region a six-character code composed of alternating letters (not including D, F, I, O, Q, and U) and digits, such as P7B5E1 and K7L3N6. Discuss the advantages that this scheme has over the five-digit ZIP code used in the United States.

73.

The Canadian scheme detects any transposition error involving adjacent characters. Also, because the Canadian code has 6 characters and there are more than 10 choices for the alphabetic characters, there are many more possible Canadian codes than U.S codes. Hence, the Canadian scheme can target a location more precisely.

Question 16.104

74. Given that the letters D, F, I, O, Q, and U are not used in the Canadian postal code (see the previous exercise), determine the maximum possible number of postal codes.

Question 16.105

75. Determine the Soundex code for the names Hu, Lee, and Shaw.

75.

H-000; L-000; S-000

Question 16.106

76. Determine the Soundex code for Skow, Sachs, Lennon, Lloyd, Ehrheart, and Ollenburger.

Question 16.107

77. Determine the total number of codes possible using the Soundex Coding System.

77.

$26 \cdot 7^{3} = 8918$

Question 16.108

78. Explain why none of the following blocks of digits can be a Soundex code for someone’s last name: S-205, S-723, S-5513.

Question 16.109

79. In Florida, the last three digits of the driver’s license number of a female with birth month $m$ and birth date $b$ are $40 (m - 1) + b + 500$ . For both males and females, the fourth and fifth digits from the end give the year of birth. Determine the last five digits of a Florida driver’s license number for a female born on July 18, 1942.

79.

42758

Question 16.110

80. Thinking of the last three digits of a Florida driver’s license number as a 3-digit integer, what is the largest possible integer it can be?

Question 16.111

81. Suppose two females with Florida driver’s licenses were born exactly one month apart. By how much would the 3-digit integers represented by the last three digits of their driver’s license numbers differ?

81.

By 40 if they are the same gender; by 540 if they are different genders.

Question 16.112

82. Describe a situation in which the 3-digit integers represented by the last three digits of the Florida driver’s licenses of identical twins could differ.

Question 16.113

83. Explain why an Illinois driver’s license number that ends with the last five digits 03217 is suspicious.

83.

The digits 03 indicate that the person was born in 1903 or 2003.

Question 16.114

84. Determine the last five digits of an Illinois driver’s license number for a male born on June 18, 1942.

Question 16.115

85. In Illinois, one obtains the last three digits of the driver’s license number for a female by adding 600 to the number for a male with the same birthday. In Florida, 500 is added to the number for a male. Why can't Florida use 600?

85.

For a woman born in November or December, the formula $40 (m - 1) + b + 600$ gives a number requiring four digits.

Page 697

Question 16.116

86. Explain why an Illinois driver’s license number that ends with 77061 cannot be valid.

Question 16.117

87. Determine the birth date of a person whose Illinois driver’s license number ends with 58818.

87.

August 1, 1958

Question 16.118

88. Provide three names that share the same Soundex code as Gallihan.

Question 16.119

89. The state of Washington encodes the last two digits of the year of birth into driver’s license numbers (in positions 8 and 9) by subtracting the two-digit number from 100. For example, a person born in 1942 has 58 in positions 8 and 9, whereas a person born in 1971 has 29 in positions 8 and 9. Speculate on the reason for subtracting the birth year from 100.

89.

Since many people do not like to make their age public, this method is used to make it less likely that people would notice that the license number encodes year of birth.

Question 16.120

90. Apply the Soundex code to common ways to misspell your name. Do they give the same code as your name does?

Question 16.121

91. Why would the Soundex system of coding be a poor method for encoding names in China?

91.

Because of the short names and large population, there would be a significant percentage of people whose names would be coded the same.

Chapter Review

Question 16.122

92. Explain why an error caused by transposing any two digits of an American Express Travelers Cheque is not detected by the check-digit scheme.

Question 16.123

93. Determine the Soundex code for Smith, Schmid, Smyth, and Schmidt.

93.

S 530 for each name

Question 16.124

94. Driver’s license number-assignment schemes that use personal data sometimes produce the same number for different people. Speculate about circumstances under which this is more likely to occur.

Question 16.125

95. When using the travelers cheque, credit card, or UPC number algorithms for detecting errors, does the computer have to know which digit is the check digit?

95.

The computer need not know which digit is the check digit because it merely checks to see if the weighted sum is divisible by 9 for traveler’s checks and divisible by 10 for the other two.

Question 16.126

96. Change 173 into a Postnet code.

Question 16.127

97. The following is an actual identification number and bar code from a roll of wallpaper. What appears to be wrong with them? Speculate on the reason for the apparent violation of the UPC format.

Building Regulations: 1985 Class 0
FINE ART WALLCOVERINGS LTD.
HOLMES CHAPEL, CHESHIRE
MADE IN ENGLAND
FABRIQUE EN ANGLETERRE

97.

The manufacturer’s number and the product number are 6 digits long instead of 5. This bar code is the European article number bar code.

Question 16.128

98. Explain why the last three digits of a valid Illinois driver’s license cannot be 373.