17.4 17.3 Data Compression
Binary linear codes are fixed-length codes. In a fixed-length code, each code word is represented by the same number of digits (or symbols). In contrast, Morse code (see Spotlight 17.3), designed for the telegraph, is a variable-length code, that is, a code in which the number of symbols for each code word may vary.
708
Morse Code Spotlight 17.3
Morse code is a ternary code consisting of short marks, long marks, and spaces (see figure at right). It was invented in the early 1840s by Samuel Morse as an efficient way to transmit messages using electronic pulses through telegraph wires. The code enabled operators to send strings of short pulses, long pulses, and pauses representing characters transformed into indentations on paper tape that could be easily converted back to characters. Although Morse code was widely used up until the mid-twentieth century, it has gradually been supplanted by more machine-friendly codes. Because Morse code uses data compression, sending messages using Morse code is faster than text messaging. Many Nokia cell phones can convert text messages to Morse code.
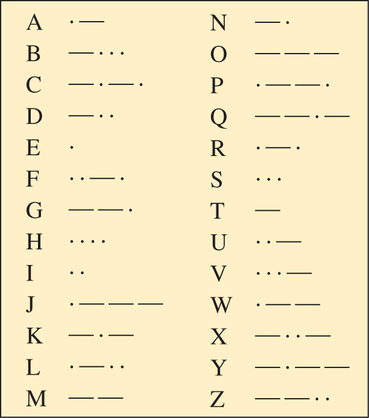
Notice that in Morse code, the letters that occur most frequently are represented by the fewest number of symbols, whereas letters that occur less frequently are coded with more symbols. By assigning the code in this manner, telegrams could be created more quickly and could convey more information per line than could fixed-length codes, such as the binary code for Postnet code (discussed in Section 16.3), where each digit from 0 through 9 is represented by a string of length 5. Morse code is an example of data compression.
Data Compression DEFINITION
Data compression is the process of encoding data so that data are represented by fewer symbols.
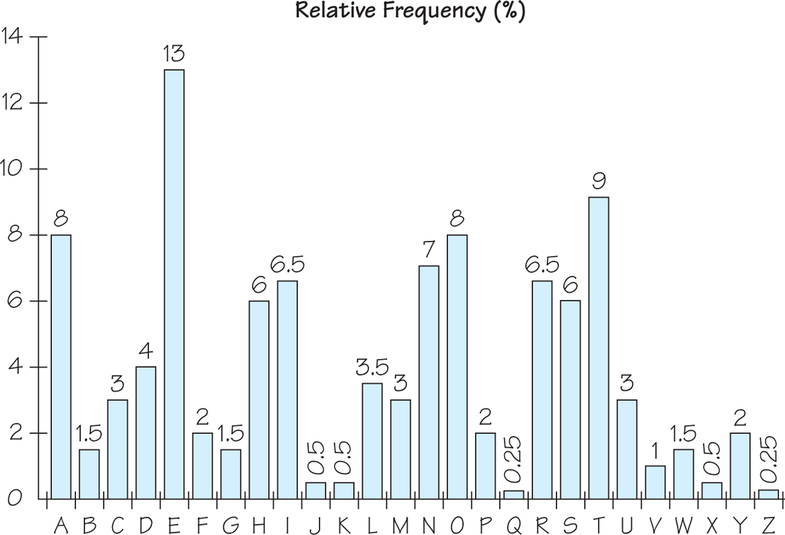
Figure 17.9 shows a typical frequency distribution for letters in English- language text material.
Data compression provides a means to reduce the costs of data storage and transmission. A compression algorithm converts data from an easy-to-use format to one designed for compactness. Conversely, an uncompression algorithm converts the compressed information back to its original (or approximately original) form. Downloaded files in the ZIP format are an example of a particular kind of data compression. When you “unzip” the file, you return the compressed data to its original state. In some applications, such as datasets that represent images, the original data need only be recaptured in approximate form. In these cases, there are algorithms that result in a great saving of space. Graphics Interchange Format (GIF) encoding returns compressed data to its exact original form, while Joint Photographic Experts Group (JPEG) encoding and Motion Picture Expert Group (MPEG) encoding return data only approximately to its original state.
709
EXAMPLE 6 Data Compression
Let’s illustrate the principles of data compression with a simple example. Biologists are able to describe genes by specifying sequences composed of the four letters , , , and , which represent the four nucleotides adenine, thymine, guanine, and cytosine, respectively. One way to encode a sequence such as in fixed-length binary form would be to encode the letters as
The corresponding binary code for the sequence is then
On the other hand, if we knew from experience that occurs most frequently, second most frequently, and so on, and that occurs much more frequently than and together, the most efficient binary encoding would be
For this encoding scheme, the sequence is encoded as
Notice that the encoded sequence in Example 6 has 20% fewer digits than our previous sequence, in which each letter was assigned a fixed length of 2 (16 digits versus 20 digits). However, to realize this savings, we have made decoding more difficult. For the binary sequence using the fixed length of two symbols per character, we decode the sequence by taking the digits two at a time in succession and converting them to the corresponding letters.
The following observation explains the algorithm for decoding our compressed sequences. Note that 0 occurs only at the end of a code word. Thus, each time you see a 0, it is the end of the code word. Also, because the code words 0, 10, and 110 end in a 0, the only circumstances under which there are three consecutive 1s is when the code word is 111. So, to quickly decode a compressed binary sequence using our coding scheme, insert a comma after every 0 and after every three consecutive 1s. The digits between the commas are code words. Example 7 illustrates the method.
710
EXAMPLE 7 Decode 0001001111100010
Inserting commas after every 0 and every occurrence of a block 111, we have 0,0,0,10,0,111,110,0,0,10. Converting these characters to letters, we obtain .
EXAMPLE 8 Code and Decode the Result
Recall: , and . So
To decode the encoded sequence, we insert commas after every 0 and after every occurrence of 111 and convert to letters:
Self Check 3
Using the coding scheme
convert the sequence into binary code.
Given the encoding scheme
decode the binary string 0101110111010.
- 10101101110, ACGAGAC
Delta Encoding
For datasets of numbers that vary little from one number to the next, the method of compression called delta encoding works well.
EXAMPLE 9 Delta Encoding
Consider the following closing prices (rounded to the nearest integer) of the Standard & Poor’s (S&P) index of the stock prices of 500 companies in July 2013:
| 1615 | 1614 | 1615 | 1632 | 1640 | 1652 | 1653 | 1675 | 1680 | 1683 | 1676 |
| 1681 | 1689 | 1692 | 1696 | 1692 | 1686 | 1690 | 1692 | 1685 | 1686 | 1686 |
711
These numbers use 108 characters in all (counting spaces). To compress this dataset using the delta method, we start with the first number and continue by listing only the change from each entry to the next. So our list becomes
| 1615 | −1 | 1 | 17 | 8 | 12 | 1 | 22 | 5 | 3 | −7 | 5 | 8 | 3 | 4 | −4 | −6 | 4 | 2 | −7 | 1 | 0 |
This time we have used only 52 characters, counting the minus signs, to represent the same data, a savings of almost 52%.
Self Check 4
Given that the following numbers were encoded using the delta function, determine the original numbers:
| 1020 | 15 | 12 | −6 | 8 | 20 | −4 |
Huffman Coding
The coding methods we have shown so far are too simple for general use, but in 1951, a graduate student named David Huffman (see Spotlight 17.4) devised a scheme for data compression that became widely used. As in the first compression scheme we discussed, Huffman coding assigns short code words to the characters with high probabilities of occurring and long code words to those with low probabilities of occurring. A Huffman code is made by arranging the characters from top to bottom in a so-called code tree according to increasing probability; it proceeds by combining, at each stage, the two least probable combinations and repeating this process until there is only one combination remaining.
David Huffman Spotlight 17.4
In 1951, David Huffman and his classmates in an electrical engineering graduate course on information theory were given the choice of writing a term paper or taking a final exam. For the term paper, Huffman’s professor had assigned what at first appeared to be a simple problem: Find the most efficient method of representing numbers, letters, or other symbols using binary code. Huffman worked on the problem for months, developing a number of approaches, but he couldn’t prove that any of them were the most efficient.
Just as he was about to throw his notes in the garbage, the solution came to him. “It was the most singular moment of my life,” Huffman says. “There was the absolute lightning of sudden realization. It was my luck to be there at the right time and also not have my professor discourage me by telling me that other good people had struggled with the problem,” he says. When presented with his student’s discovery, Huffman recalls, his professor exclaimed: “Is that all there is to it?!”
“The Huffman code is one of the fundamental ideas that people in computer science and data communications are using all the time,” says Donald Knuth of Stanford University. Although others have used Huffman’s encoding to help make millions of dollars, Huffman’s main compensation was dispensation from the final exam. He never tried to patent an invention from his work and experienced only a twinge of regret at not having used his creation to make himself rich. “If I had the best of both worlds, I would have had recognition as a scientist, and I would have gotten monetary rewards,” he says. “I guess I got one and not the other.”
David Huffman died October 7, 1999.
Source: Excerpted from the article “Profile: David Huffman” by Gary Stix, Scientific American, September 1991, pp. p. 54 p. 58.
712
EXAMPLE 10 Huffman Code
To illustrate the Huffman method, say we have six letters of a dataset that occur with the following probabilities:
Rearranging them in increasing order, we have:
Because and are the two letters least likely to occur, we begin our tree by merging them with the one with the smallest probability on the left (i.e., rather than ), adding their probabilities, and rearranging the resulting items in increasing order:
This time, and are the two least likely remaining entries, so we merge them with on the left (because it has smallest probability), add their probabilities, and re-sort from smallest to largest. This gives:
Next, we combine and with on the left and re-sort to get:
Then we combine and with on the left and re-sort again:
And finally we combine and with on the left to obtain:
713
To create the Huffman tree, start with a vertex at the top labeled with the final string 1.000, then reverse the steps used to merge letters to work your way down the tree by creating two branches corresponding to each merger of the two least likely entries at each stage; assign 0 to the branch with the lower probability and 1 to the other branch, as shown in Figure 17.10. To assign a binary code word to each letter, we follow the path from the end of the tree to each letter by assigning, at each merging juncture, 0 or 1 according to the label on the branch taken. Thus, we have
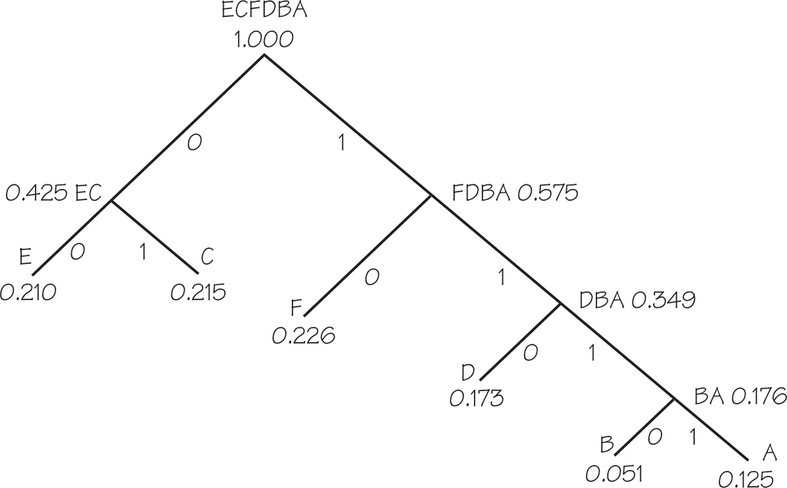
Notice that the letters that occur least often have the longest codes and the letters that occur most often have the shortest codes.
Decoding codes created from a Huffman tree is possible because there is only one way a particular string could have occurred. Consider the Huffman code created using the code words given in the preceding display:
How can we determine the corresponding string of letters that has this Huffman code? The method is quite simple. Starting at the beginning of the string, every time we find a code word, we replace that string with its corresponding letter (, , , , , or ) and continue. Since all of our code words have at least two digits, we look at the first two digits. If they form a code word, then replace them with the corresponding letter. If not, then look at the next digit. If the three digits form a code word, then replace them with the corresponding letter. If not, then these three digits and the next one are a four-digit code word.
714
EXAMPLE 11 Decoding a Huffman Code
Looking at our example 11101000011010011111010010, we see that neither 11 nor 111 is a code word but 1110 is the code word for . So, replacing 1110 with , we have . The next possibility is 10, which is the code word for , so we have . Next, we have 00, which is the code word for , giving us . Continuing in this way, we obtain . Of course, in practice, coding and decoding are done by computers.
Self Check 5
Decode the binary string 001101111001001 that was encoded using the Huffman code given in Example 10.
- EDAEFC